培养高中学生逆向思维能力的实践研究*
☉江苏省南通中学 陆王华
学生解题时一般都会顺着某个方向对问题展开探索,事物之间的双向性与可逆性往往被学生轻易抛诸脑后,解题思维自然会遇到重重波折.因此,教师在实际教学中应有意识地对学生进行逆向思维的培养,帮助学生学会理顺知识的内在联系,并因此使其加深对数学定义、定理、公式的理解,这对于学生的顺利解题、知识巩固来说大有裨益.
一、逆向思维的内涵
从问题的反面或否定方面对问题进行思考继而获得解题方法的思路称作逆向思维,很多不易解决的问题在运用逆向思维求解时往往会获得意想不到的效果.这种和正向思维相反的创新型思维打破了常规的思维程序,从正向思维推理的相反方向对问题展开全新思维的分析继而获得解题.
逆向思维通常可以分为缺点型逆向思维、转换型逆向思维和反转型逆向思维这三种方法,具备异常性、普遍性、新颖性等显著特点的逆向思维在解题中的运用往往能起到很好的作用与影响.
教师在培养学生逆向思维能力的实际教学中,首先应全面掌握其类型与特点并因此为后续的具体应用奠定基础.总之,从不同角度探析问题并将逆向思维与具体问题结合起来,往往能有效打破习惯性思维并顺利获得解题的突破,这对于提升学生的解题能力来说具有积极的意义.事实上,逆向思维在解题中的运用还能帮助学生更加深入地理解知识并掌握相关规律,使学生的原有思维得到创新并因此在数学学习中获得更好的学习效果.
二、逆向思维的重要价值
根据思维过程的指向性可将思维分为正向思维与逆向思维两种形式,正向思维在高中数学解题中的运用虽然能够取得很好的效果,但一味强调学生的正向数学思维,往往会令学生陷入思维的僵局并在特殊问题面前束手无策.因此,逆向思维在高中数学解题中的运用也是相当重要的,教师应在具体教学中积极调动学生分析问题、解决问题的积极性并使其创新能力、逆向思维能力获得提升,为数学解题增加更多的有效思维方向与途径.
三、培养逆向思维的方式
1.公式的逆用
很多学生记忆数学公式的顺向形式往往会得心应手,但面对公式的逆向形式却感觉记忆倍加困难,运用起来也就更加生涩了.因此,教师在培养学生逆向思维能力时首先可以着眼于公式的逆用,帮助学生学会逆用公式以提升其逆向思维能力.
例1已知,试求的值.
分析:三角式中的分母是sinα、cosα 的二次齐次式,分子为1,逆用公式sin2α+cos2α=1,将分子升幂成二次齐次式并将分子、分母同除以cos2α可得
2.公式、不等式的逆向证明
很多学生在证明等式或不等式时往往习惯于从左到右进行思考,但实际上,很多问题在自右向左的证明中体现出更加简捷的思维与方法.
例2设x、y∈R,求证
分析:证明本题的方法不只一种,不过在利用|x+y|≤|x|+|y|并自右向左进行证明时,简捷的思路令人耳目一新.
证明:若|x+y|=0,则所要证明的不等式成立是明显的事实.
若|x+y|≠0,则:
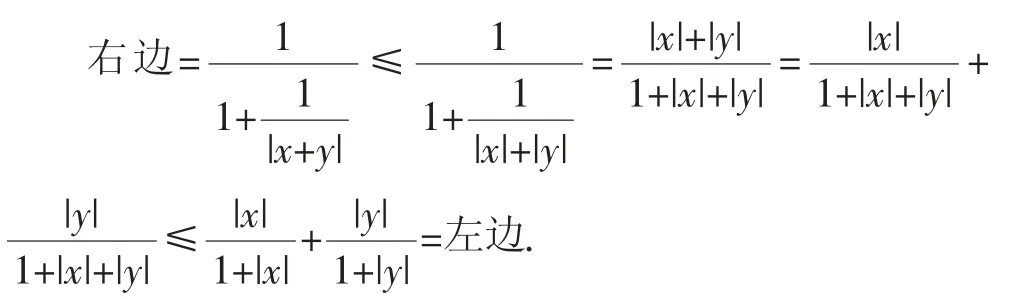
3.由简到繁的证明
很多证明题的推导过程都是由繁至简的,但有些个别问题的证明在由简到繁的证明中却更显简捷性.
例3求证sin2α·tanα+cos2α·cotα+2sinα·cosα=tanα+cotα.
分析:运用由繁至简的原则对此题进行从左到右的证明也是可行的,但从简到繁地对此题进行证明却更加别致而快捷.
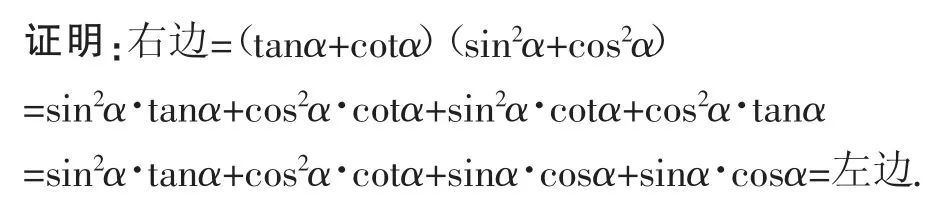
4.分子有理化
很多学生因为思维定势的原因只明白需要将分母有理化,但实际上,对分子有理化也是解决有些问题经常会用到的独特方法.
例4试求函数的值域.
分析:运用三角替换也可以求得该函数的值域,但相对复杂,如果联系函数的单调性并将分子有理化则会令求解更为简便.
解:当x≤-2 时,y 是x 的增函数,所以y≤-2;
5.反面思考法
有些问题从正面思考往往会显得复杂,但如果从反面进行思考会获得令人耳目一新的简捷方法.
例5某班共有学生45 名,如果将每位学生在一年365 天中任意一天出生的概率看作一样,则该班至少有2 位学生生日相同的概率是多少?
解析:从正面对此题进行分析,需要考虑恰巧有2人、3 人、4 人…直到45 人生日都相同的情况,麻烦自不必说.但如果从反面展开思考,利用45 名学生中任两人生日均不相同的可能情况来解题,题目就会简单很多,任意两人生日均不相同的概率为,则所求概率为
6.反证法
从正面直接证明相对困难时不妨试试反证法.
例6求证:方程x2-2019x+2021=0 不存在整数解.
分析:运用求根公式来证明此题虽然可行,但过程太过繁杂,显然是不可取的.因此,不妨运用逆向思维,从反面对此题进行证明.
证明:设原方程存在整数根,因为Δ>0,因此方程存在相异实根x1、x2,则:
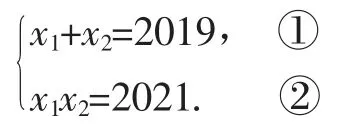
由①可知,x1、x2不可能存在一个是整数根、一个是非整数根的情况.再根据②可知,x1、x2一定均为奇数,和①明显矛盾了.
所以,该方程是不存在整数根的.
7.分析法
解题时应尽量探索正确的解题方向,这也是解题的出路,因此,充分利用问题结论的指向作用并进行逆向思考,往往会令解题者从结论上分析获得解题的方向.
例7求证
分析1:分析法并将分子进行有理化,即可得出:

分析2:分析法并结合移项、两边平方、化简,可得:

所以原不等式成立.
总之,教师引导学生借助全新的视角对问题展开分析,引导学生从结论出发进行逆向思考,以及问题的分析与处理,帮助学生打破习惯性的思维定式并获得更加灵活有效的解题方法,是培养学生逆向思维能力的有效思路与举措,教师对学生逆向思维的关注与培养能使其数学综合素养得到有力的提升.因此,高中数学教师应牢牢把握高中学生思维发展的上升与成熟阶段加强学生数学逆向思维的培养,帮助学生在深入理解、分析数学知识的过程中对知识形成全面的理解,有效拓宽学生的数学学习思路,并使其掌握不同角度、方向进行问题分析与处理的方法,以促进学生逆向思维能力的提升.

