正确认识，深刻理解，训练有“素”，方可滋“养”——对“数学运算”核心素养的思考

☉浙江省杭州第四中学 来丽莹

学科核心素养被称为继课程改革之后基础教育最重要的研究成果.《普通高中数学课程标准（2017 年版）》明确把“数学运算”列为数学六大核心素养之一.“数学运算不是一个简单的运算，而是基于有效方法去解决问题的过程，即在明晰运算对象的基础上，依据法则解决数学问题的素养”.良好的数学运算素养好比是一把解决问题的金钥匙，有了它，解决问题的速度和正确率会大大提高.然而在实际教学过程中，学生数学运算中“会而不对，对而不全，全而不优”的现象比比皆是，严重制约了学生数学能力的提升.因此正确认识“数学运算”，切实培养学生的运算素养、提高学生的运算能力，成为当今数学教学的重中之重.

一、“数学运算”的教育价值

1.数学运算贯穿数学学习的全过程

从小学阶段学习数的运算，到中学阶段学习式的运算，再到高等数学中要通过运算来认识和建构群、环和域等数学结构，以及更为抽象的数学空间.可见数学运算贯穿数学学习的全过程，也是一个由浅入深、由表及里的循序渐进的过程.

2.数学运算素养反映并发展了其他数学核心素养

数学运算是利用运算解决数学问题的过程，在这个过程中，学生首先要分析运算对象，再确定运算的方向，进而选择合适的运算法则，最后得到运算结果.这些过程中，逻辑推理、数学抽象都起到了至关重要的作用，有时候也需要一些数学的直观想象和数学建模的思想.整个运算的过程本身又是一个数据分析的过程.因此，数学运算可以说是其他所有数学核心素养的集中呈现过程，发展数学运算素养就是提高学生整体的数学素养.

二、“数学运算”的主要体现形式

1.深刻理解运算对象

在解决数学问题的过程中，首先要明确对谁进行运算，了解运算对象的背景，理解运算对象的实质、几何意义及相关联的概念等，并在运算过程中加深对运算对象的再理解和再认知.

例1存在函数f（x）满足：对于任意x∈R 都有（ ）.

A.f（sin2x）=sinx B.f（sin2x）=x2+x

C.f（x2+1）=|x+1| D.f（x2+2x）=|x+1|

看到此题，很多学生无从下手，无法辨别运算的对象是什么，推及原因表面上是因为此题的形式很新颖，但本质上是学生对函数定义没有深刻地理解.函数的定义从初中用变量之间的依赖关系——函数的“变量说”进一步抽象到用集合语言和对应关系刻画函数——函数的“对应关系说”，这是思维深度上的一次重大升华.因此，在平时学习中只有对函数定义的内涵即“一种特殊的对应关系”深刻理解、了然于心，才能透过现象看到此题的本质.

因此对运算对象及其特征做到心中有数，明确运算对象的内涵与外延是运算顺畅进行的第一步.

2.灵活掌握运算法则

运算法则是运算过程与结果正确性的保障，学生需要熟记相关的数学必备知识.但同时不能生硬地照搬照抄，而是要在理解的基础上进行灵活运用.高中很多数学问题的解决需要用到连续的恒等变形，这个过程需要学生从不同的角度运用运算的法则和技巧.

例2已知sinβ=msin（2α+β），求证：tan（α+β）=·tanα（m≠1）.

本题的难点在于此题出现了多个角和不同的三角函数名.有学生在证明的过程中，先将目标式切化弦，再运用两角和的公式展开，最后寻找条件式和目标式的等价关系.整个运算过程相当复杂，不容易算正确.其实应该先观察已知角和目标角之间的关系：β=（α+β）-α，2α+β=（α+β）+α，通过变角得到sin［（α+β）-α］=msin［（α+β）+α］，再通过两角和的正弦公式进行变形化简.通过对比可以发现，第二种“变角”的方法更为简便，更容易得到正确的运算结果.由此可见，一样的运算法则，不同的理解，就会带来运算速度上的差异，解题的复杂程度也会不同.

3.探究不同的运算思路

运算思路是数学运算得以正确实施的关键，在它的推理过程中蕴含着丰富的逻辑性.不同的运算思路反映着不同层次的运算思维，对运算方法进行优化，选择运算步骤少、变形简单、运算量小等特点的最佳解题方案，从而便于求得正确的运算结果.

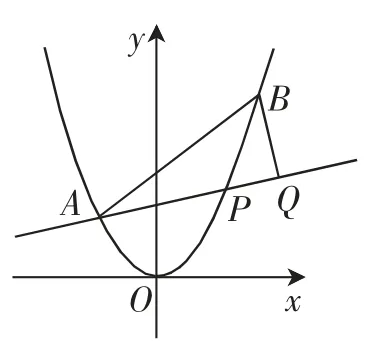
图1

例3如图1，已知抛物线x2=y，点，抛物线上的点，过点B 作直线AP 的垂线，垂足为Q.

（1）求直线AP 的斜率的取值范围；

（2）求|PA|·|PQ|的最大值.

本题第二问（第一问略）中|PA|的长度易得，难点在于|PQ|长度的表达，无论是用两点之间距离公式，还是勾股定理，计算过程都相当复杂.再观察一下目标式：|PA|·|PQ|，是两个长度相乘，于是尝试用向量视角解决这个问题.

三、落实“数学运算”素养的教学策略

1.完善学生认知结构，夯实运算基础

（1）重视数学必备知识的教学.

数学必备知识是数学学科中的核心概念、法则、公式、性质等知识，是数学运算得以正常实施的基础.学生数学运算的速度和准确率与必备知识掌握得是否准确直接相关.在数学必备知识的教学中，必须重视知识的发生和发展过程.

例如：在《椭圆及其标准方程》的教学中，一定要注重椭圆概念的形成过程，通过学生自己动手实验和观察几何画板动画，引导学生自我归纳椭圆的定义，学生通过不断的“试错”、修改、补充，一步步完善椭圆的定义，在这由表及里、去伪存真的过程中学生不仅理解了椭圆的定义，而且提高了逻辑推理、抽象概括等能力，这些都是发展数学运算素养的保障.

同时，教师要经常带领学生进行知识归类整理，把一些通性通法进行梳理归纳，通过适度的重复练习形成数学技能，以便解题时能在短时间内自动检索筛选，获得解题的思路，从会学习的角度看，学生就获得了数学素养的提高.

（2）及时纠正学生运算偏差.

学生的认知结构是动态发展的，尤其在知识的初生长阶段，可能因为自己的理解不透彻和掌握不熟练而出现运算错误，此时教师必须帮助学生分析出错的原因，切不可一句“仔细点”而轻描淡写地带过.

例4设首项为1 的等差数列{an}的前n 项和为Sn，已知数列的前n 项和为，等比数列{bn}满足公比q＞1，b1=4，且b4是3b3，2b2的等差中项.求数列{an}和{bn}的通项公式.

本题并不很难，但不少同学做错，仔细查看解答过程才发现他们把理解成了“数列的通项公式”，这不能用简单的“看错”来归因.分析后，才发现是因为题设中的“Sn”成了干扰因素，导致学生把通项公式和前n项和公式混淆.本质还是对“数列”概念的理解出了错，除纠正错误以外，还要教给学生利用换元的思想“令从而换成“数列{cn}的前n 项和为，这样概念就会清晰很多，错误率也会大大减少.

因此，在数学认知结构的形成过程中，及时纠正运算错误，探究原因，不仅可以使教师了解学生已有的认知结构，更可以促进学生理解水平的提高，从而提高运算的素养.

2.优化学生的思维品质，提高运算的灵活性

（1）注重运算思路探究的教学.

运算思路是数学运算的核心，教会学生如何探究运算思路是解决数学问题的关键.探究运算思路要理解题意，明确运算的对象，知晓运算道理，能进行概念之间、定理之间、性质之间的相互转化.从“问题”开始，直至“问题”结束，在此过程中教会学生如何探究解题思路：此题已知条件是什么？要得到结论需要什么条件？与已知条件之间的关系是什么？条件和结论该如何转化？这个题与以前做过的哪些题类似？解决这类问题的主要途径有什么？能否进行数与形的转化等.

例5已知函数f（x）=-x2-（2-a）x+alnx，a∈R.当a＞0 时，若x1，x2为函数的两个零点，x3为函数f（x）的极大值点，且x1＜x2，证明：

在此题的讲解过程中，教师可以引导学生做以下层层分析：

①由问题中的条件可得什么结论？答：可得-x12-（2-a）x1+alnx1=0；-x22-（2-a）x2+alnx2=0

③有这个新创的条件，结论可以如何转化？答：利用分析法通过代入化简进行证明，要证x3＞，即证

“授人以鱼，不如授人以渔”，因此，教师在解题教学中要充分展示对数学运算对象的理解过程，让学生积极参与整个探索数学运算思路的过程，使学生有体会、有感悟、有收获、有创新！

（2）重视运算过程的优化教学.

高中的数学题往往是“宽口径”，即解决方法不止一种，对运算对象的不同理解就会产生不同的运算路径.实际教学中，学生容易陷入一种运算思路，经常因为烦琐的运算过程导致不能得到正确的计算结果.因此，教师要带领学生经历数学知识的整合过程，站在数学学科整体高度上优化知识结构，强化对数学必备知识本质的理解与应用意识的培养，提高学生分析问题、解决问题的能力.

总之，要有效培养学生的“数学运算”素养，作为教师就要深刻理解数学运算的含义，把运算能力的培养渗透到每一节课的每一道题中.通过精心设计教学内容，帮助学生深刻理解概念的内涵和外延，并注重整合各个知识点，多角度、多层次地探究解题思路，启发学生数学思维，适时讲解、反复强调，努力让学生形成良好的运算心理意识和品质！