高中数学核心素养在习题教学中的体现
☉广西壮族自治区贺州市平桂区平桂高级中学 朱远彰
自新课改实施以来,教育部门颁布了多项政策来促使教师在教学中重点关注学生的学科核心素养,即所有课程的设置都应涵盖思考、体验和表达教育.思考教育,指在学习上对学生加强引导,增强其独立思考的能力,并反思自己的得与失;体验教育,指在学生做题时给予一定的指导和帮助,梳理做错的习题,归纳其中的内在规律,由此让学生迅速掌握正确的方法,提升做题的正确率及缩减做题时间;表达教育,指在课堂教学中应留出给学生交流和探讨问题的时间,鼓励学生当众解题,以此为范例指出解题中存在的问题.此外,还应坚持具体问题具体分析的原则,点明同一类型的题目在不同情况下的问题,哪些知识点需要写哪些知识点不需要写.综上所述,培养学生的核心素养不仅要传授正确的解题思路,还要让学生掌握相应的解题方法.
一、核心素养内涵
(1)数学核心素养符合高中数学教学的基本规律,且有利于自身的全面发展及提高将来走向社会后适应社会的能力.尤其是在新课改的大背景下,教师不仅要让学生掌握最基本的数学原理,还要培养他们的数学思维,提升数学素养,这对其他学科的学习也大有裨益.高中数学知识相比初中难度更大、教学任务更加繁重,对学生提出了更高的标准和要求,所以教师应将数学核心素养的培养贯彻到教学的全过程,让学生在掌握知识的同时也能够提升思维能力和数学素养,以便更好地应用于实践生活中.
(2)高中数学核心素养的重要性.
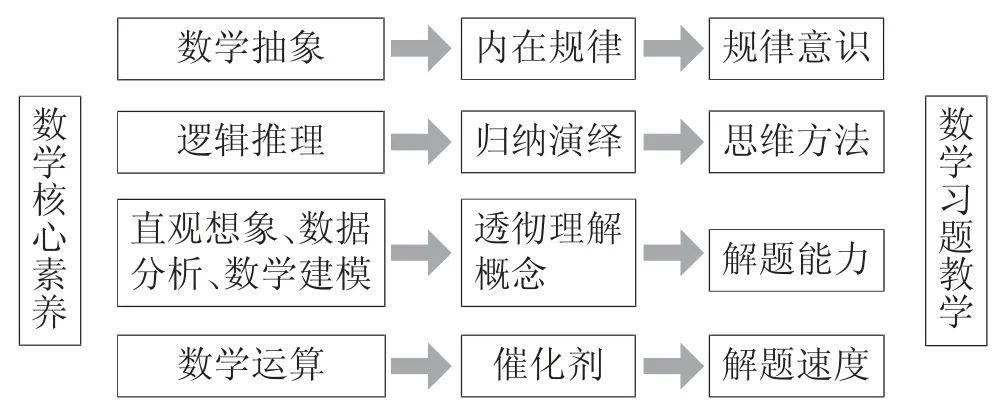
高中生应该具备的核心素养主要表现在情境和问题、思维和表达、知识和技能、交流和反思.这些素养不仅有助于提升学生的解题能力,也有助于解决日常生活中常见的问题,为将来更好、更快地适应社会打好坚实的基础.抽象思维的利用能够让学生在具体问题中找到内在规律,以此形成规律意识;逻辑推理则让学生在归纳和演绎中形成独特的思维方法;而直观想象、数据分析和数学建模更是从数学的角度让学生透彻理解理论和概念,由此提高解题和做事的能力;数学运算则是解决所有习题的催化剂,加快做题速度,通过熟练的运算能力将解题思路完全地展示出来.
二、高中数学习题教学中核心素养的培养策略
(一)训练良好的解题思维
提升学生的逻辑推理能力应该从学生的实际情况入手,采取直观、自然的方法分析问题,从学生的视角解题,这样得到的结果才符合学生的认知,学生才能提升逻辑思维能力,获得更加多样化的解题途径.如数列中有种题型会考查证明含有数列通项公式的不等式成立,这类题目就要学生通过自己的逻辑推理能力及数学抽象能力来推断不等式的规律,并进行归纳演绎.
例1等比数列{an}的前n 项和为Sn,已知对任意的n∈N*,点(n,Sn),均在函数y=bx+r(b>0且b≠1,b,r均为常数)的图像上,对任意的n∈N*,当b=2时,记bn=2(log2an+1),证明:对任意的n∈N*,不等式成立.
证明:通过解题得知r=-1,bn=2(log2an+1)=2(log22n-1+1)=2n.
此时就可以应用多种思路进行解题,首先学生最常用的就是数学归纳法:
方法1:(1)当n=1 时,,因为,所以不等式成立.
(2)假设当n=k 时不等式成立,

根据(1)和(2)可知,对任意的n∈N*,不等式都成立.
方法2:也可应用放缩法.

方法3:均值定理.

教师在教学中不应仅仅局限于公式的套用,应将点明解题思路放在首位.数学题的教学更应注重方法及其推导过程.核心素养的存在就是集体思维的整体展示,要打开学生的解题思维,不拘泥于一种解题方法,注重一题多解,找到更加多样化的解题方法.
(二)加强过程指导,提高思维能力
数学习题的教学是师生双方互动的过程,以教师教学作为途径,以学生掌握做题的基本方法为目的.所以,应选择与学生情况相符合、难度适中的数学题,这样既不会让学生感到没有挑战性,也不会产生畏难情绪.不仅能够提升学生学习的积极性,还能优化和完善学习方法,在解题中锻炼和提升学生自主学习的能力,保障以后开展自主学习的效果.
教师在设计活动式情境时应保持同数学习题发展方向的一致性.趣味性是活动式情境的最典型的特征,尽管其中包含游戏成分,但仍需学生具备较强的思维水平,只有这样才能深入了解数学基本概念,保障学习效果.
(三)横向拓展
现代思维科学的研究表明,思维是问题产生的源头,也是推动创新的重要动力.要让学生在学习中学会质疑权威,由此提升学生发现问题、分析问题和解决问题的能力.
例如,在开展直线和圆的位置关系这一新课程的教学中,教师在设计习题时应该秉持着从容易到困难的原则,通过阶梯式的题目设置来开阔学生的思维,由此让学生掌握基本概念和解题方法,拓宽了情境内涵的意义,由此将以往学过的、零碎的知识点串联成一个整体.如例2,可以先由圆心到直线的距离开始入手,进而教师带出圆与直线有几种位置关系;再加深难度,例3通过直线与圆的位置关系来进行数形结合,求解直线的方程;教师再继续通过综合性习题考查学生几何知识与代数之间的转换.
例2(难度*)圆(x-1)2+y2=1的圆心到直线y=的距离是( ).
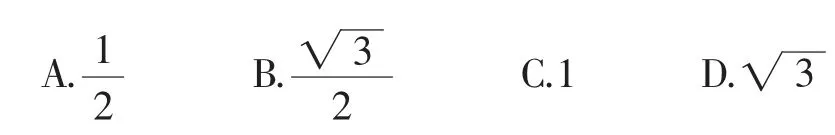
分析:选A,圆心(1,0),应用点到直线的距离公式求解.
例3(难度**)过原点的直线与圆x2+y2+4x+3=0相切,若切点在第三象限,则该直线的方程是______.
解析:设T为切点,因为圆心C(-2,0),因此CT=1,OC=2,△OCT 为直角三角形.如图1,所以∠COT=30°.所以直线OT 的方程为

图1
总结:
随着新课程的改革和素质教育理念的推进,学生自主学习能力逐渐成为评价体系中的重要元素,这就对其核心素养提出了更高的要求.核心素养是高中教育的精髓,不能提升学生核心素养的教育是失败的教育.所以在数学习题课堂教学中,教师应该树立正确的教学理念,采用合理的教学方法.为此,笔者认为应当积极为习题教学创设趣味性的情境,从宏观和微观两个角度切实解决好教师教学、学生解题中的相关问题.

