拓展高中学生数学思维空间的教学思考
☉江苏省灌云高级中学 陶中亚
学生在知识的掌握与能力的发展上很可能并不同步,学生能力的发展必须建立在掌握知识这一基础与前提之上,但这并不意味着能力的形成与发展只要堆积知识就可以实现,学生的思维能力需要知识的积累及学习过程中的不断探索.
新课标理念下的教育思想侧重于知识传授与能力培养的双重发展,因此,教师在实际教学中应着眼于学生知识和能力的相互促进,帮助学生有效积累基础知识并使其实验观察能力、逻辑思维能力、自学能力、创造能力获得长远的发展,在教学中关注学生情感、意志、毅力、性格等非智力因素的发展并使其获得全方位的提升.因此,学生思维空间的拓展及思维能力的培养是高中数学教师必须重点关注的内容.
一、巧设解题“陷阱”
很多学生因为缺乏思考而在数学问题的处理上不能获得周全、准确的结论,教师有意设计的解题“陷阱”能够有效帮助学生在激烈的思维碰撞中加深对数学概念和规律的理解、辨析与刻画.
例1已知数列{an}是等比数列,其中a3=3,S3=9,则数列{an}的公比q 为多少?
上述题目对于初学等比数列求和公式的学生来说是一道简单题,但学生在此题实际求解过程中的表现却令笔者诧异,很多学生的解题出现了错误.探究学生的错误,我们发现学生没有注意到等比数列求和公式的适用条件是他们解题产生错误的主要原因,学生在解题中直接使用了公式并漏掉了公比q=1 的情况,令解题正确率偏低.
二、挖掘题目内涵
引导学生树立明确目标、探索条件的思维方式并使其对题目的内涵展开深入的挖掘,能使学生的发散思维能力得到很大的提升,使其思路更加活跃并能够提升其学习的效率.
例2已知向量a=(3,-4),a+b=(4,-3).
(1)试求向量a 和b 的夹角θ 的余弦值;
(2)对p、q 两个向量,若存在不全为零的常数α、β,使αp+βq=0,则称向量p 和q 线性相关,反之则称为线性无关.那么向量a、b 属于线性相关还是线性无关呢?
解析:(1)因为a=(3,-4),a+b=(4,-3),所以b=(1,1).所以
(2)如果向量a、b 线性相关,那么存在不全为零的常数α、β,使αa+βb=0,即(3α+β,-4α+β)=(0,0).故,解得这α、β不全为零相矛盾.所以向量a、b 线性无关.
三、一题多解训练
精心设计一题多解的教学训练能够有效帮助不同层次的学生获得有意义的拓展和提升,帮助学生拓宽思路并使其求异思维能力获得长远的发展.
例3已知α、β 是锐角,sin(α+β)=2sinα,求证:α<β.
解决此题应从三角函数值的相等关系推出角度的不等关系,涉及的领域从概念和运算关系来看是比较广泛的,此题的解决对于拓展学生的思维能够起到很好的作用.此题的不同证法如下.
证法1:着眼于解决此题的一般方法并进行迁移.
因为α、β 是锐角,所以结论α<β 与sinα<sinβ 是等价的.
因为sin(α+β)=sinαcosβ+cosαsinβ,所以sin(α+β)<sinα+sinβ.
又因为sin(α+β)=2sinα,所以2sinα<sinα+sinβ.所以sinα<sinβ.所以α<β.
证法2:着眼于此题中有关三角、几何的有意义的细节,以及特殊因素进行解题,在直径是1 的圆内作角α、β,如图1 所示.
BC=sinα,BD=sinβ,CD=2Rsin(α+β),即CD=sin(α+β).
因为BD>CD-CB,所以sinβ>sin(α+β)-sinα=sinα.所以β>α.

图1

图2
证法3:将α、β 看作△ABC 的两个锐角,如图2 所示.
证法4:用反证法进行证明,由α=β 或α>β 推出矛盾,证得α<β,证明过程略.
类似上面的训练能很好地激发学生的数学学习兴趣,开拓学生思路的同时也使其视野得以开阔.
四、多题归一训练
很多数学问题之间存在不同程度的量的差异,但在问题的本质上往往区别不大,甚至没有区别.教师在实际教学中应精选典型习题并进行有的放矢的精讲、点拨与拓宽,帮助学生在掌握某类题目解法的同时熟练掌握其一般解题方法,凸显问题的实质和关键并帮助学生逐步积累正确的解题经验,使学生在解题训练中逐步获得举一反三、触类旁通的解题能力与思维.
例4求下列函数的值域:
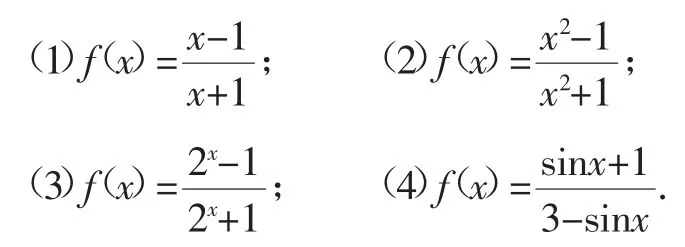
分析:求上述函数的值域,看似问题不同,但如果将(2)、(3)、(4)中的x2、2x、sinx 看成整体,那么这三个小题和(1)就成了同一类型的题目了,因此,学生只要能求出(1)中函数的值域,求解(2)、(3)、(4)中函数的值域也就不难了,不过解题过程中还是应该注意这四个小题的区别的,x、x2、2x、sinx 间的取值范围各有不同.
五、一题多问训练
训练学生串联解题能力与逻辑推理能力的一个有力举措就是一题多问,一题多问训练能帮助学生更好地深化概念或规律并令概念或规律得以升华发展,这对于发展学生的思维来说是最为有力的手段.以下例题中环环相扣的问题,着眼于学生已有知识与问题之间的联系,进行了学生思维的启发,使学生能够在相对集中的线索中展开思考与探索并获得了发散思维的锻炼,知识间内在联系得以顺利揭示的同时也令学生更好地掌握了解题的思路与脉络.
例5已知函数f(x)=x2-4,若曲线y=f(x)在点(xn,f(xn))处的切线和x 轴相交,其交点是(xn+1,0)(n∈N*),其中x1为正实数.
(1)用xn表示xn+1;
(2)求证:对一切正整数n,xn+1≤xn的充要条件为x1≥2;
(3)若x1=4,记,请尝试证明数列{an}是等差数列,并求出数列{xn}的通项公式.
对学生学好数学所应具备的思维能力的培养是高中数学教师在实际教学中最应该关注的,拓展学生的思维空间能够给予学生更多的独立思考的机会,教师应鼓励学生在解题中运用不同的思路进行解题探究并不断尝试思维的求异性,帮助学生逐步提升思维能力并引导学生学会总结、归纳一些高效思考和分析问题的方式,使学生能够在解决各种问题的过程中不断积累解题的经验并获得发挥思维能力的空间.
学生数学思维空间的拓展必须依赖有效的数学实践,也就是解题,巧设“陷阱”、一题多解、挖掘题目内涵、多题归一、一题多问等训练方式能有效发展学生的数学思维空间,教师应精心营造适合学生的数学思维环境并注重学生数学思维需求的引发,使学生在掌握一定思维方法的基础上获得更好的思维状态、思维品质并养成良好的思维习惯,这对于发展学生的思维空间来说是极为重要的前提条件.
总之,教师在实际教学中应注重学生思维能力的培养并有意识地创造出适合学生思维的空间与平台,使学生借助已有知识信息展开合理高效的思维并在迁移思维、逆向思维、求异思维、发散思维、推理思维的推动下对数学问题展开不同角度的思考、分析、解决和论证,使学生在思维迅速发展的过程中不断积累知识和解决问题的经验,帮助学生在思维和知识的相互促进、共同发展的过程中获得数学素养与能力的全方位发展.

