久考不衰隐零点,分类剖析寻思路
☉南京市第九中学 尤荣勇
函数的零点在很多时候能确定其存在,但又无法直接求解出来,这样的零点我们称之为“隐零点”.无论是在各地的高考模拟题中,还是在高考真题中,隐零点问题屡见不鲜,俨然成为压轴试题中的一道风景线.究其原因,笔者认为,它具有灵活性大、逻辑性强、综合性广的特点,是考查逻辑推理、转化与化归能力很好的素材,因而备受命题者的青睐,而这类问题又是教学中的难点之一.笔者根据自己的教学实践,对试题中隐零点问题进行题型归类、分类剖析,供同仁教学时参考,不当之处,敬请斧正,希望能起到抛砖引玉的作用.
题型一、构造函数试零点,证明超越不等式
例1(2013 年普通高等学校招生北京卷第18 题(2))求证
思维导引:作差构造辅助函数f(x)=t(x)-h(x),将原不等式证明问题转化为求f(x)的最值问题,是证明超越不等式t(x)≤h(x)的常见思路之一.
证 明:设f(x)=-x+1,则f ′(x)=-1=,不妨设g(x)=1-x2-lnx,则g′(x)=-2x-<0,所以g(x)在(0,+∞)上为减函数.又g(1)=1-1=0,所以当0<x<1时,g(x)>0,f ′(x)>0;当x>1时,g(x)<0,f ′(x)<0.所以f(x)在(1,+∞)上单调递减,在(0,1)上单调递增.所以f(x)max=f(1)=0.所以f(x)≤0 恒成立.所以≤x-1.
难点剖析:f′(x)=-1 不易判断符号,如果导函数的解析式能转化为具有分式特征且容易判断出分母符号的形式,此时往往将分子看成一个新的函数g(x),研究g(x)的符号从而得出f′(x)的符号.对于函数g(x)=1-x2-lnx,f(x)=-x+1,无法直接求其零点,首先借助函数的导数研究其单调性,再通过尝试其零点,不难发现g(1)=0,f(1)=0,原不等式证明可转化为f(x)≤0 恒成立.其中对于函数式中含有lnx 时,可试零点x=et(其中t值可根据情况而取值).
题型二、待定系数设零点,挖掘关系找联系
例2(2018 年江苏省苏州、无锡、常州、镇江市高三年级第三次联考模拟试题第19 题)已知函数f(x)=x3+ax2+bx+1,a,b∈R.若a2+b=0.
(1)当a>0 时,求函数f(x)的极值(用a 表示).
(2)若f(x)有三个相异零点,问:是否存在实数a 使得这三个零点成等差数列?若存在,试求出实数a 的值;若不存在,请说明理由.
思维导引:系数中含有参数的三次函数的零点无法直接求出,不妨通过待定系数法设出其零点,从而找出它们之间的联系.
解析:(1)由f′(x)=3x2+2ax+b 及a2+b=0,得f′(x)=3x2+2ax-a2.令f′(x)=0,解得或x=-a.由a>0 知,当x∈(-∞,-a)时,f′(x)>0,f(x)单调递增;当时,f′(x)<0,f(x)单调递减;当时,f′(x)>0,f(x)单调递增.所以f(x)的极大值为f(-a)=1+a3,f(x)的极小值为
(2)当a=0 时,b=0,此时f(x)=x3+1 不存在三个相异零点.
当a<0 时,与(1)同理可得f(x)的极小值为f(-a)=1+a3,f(x)的极大值为
所以当a≠0时,要使 f(x)有三个不同零点,则必须有(,解得a3<-1 或
法一:不妨设f(x)的三个零点为x1,x2,x3,且x1<x2<x3,则:

法二:前面同法一求出a3<-1 或.不妨设f(x)的三个零点为x1,x2,x3,且x1<x2<x3,则f(x)=(x-x1)·(xx2)(x-x3)=x3-(x1+x2+x3)x2+(x1x2+x2x3+x1x3)x-x1x2x3=x3+ax2+bx+1,则-(x1+x2+x3)=a.又三个零点x1,x2,x3成等差数列,所以-3x2=a,x2=.又,解得,所以存在这样实数a,且
难点剖析:法一设出函数三个隐零点,代入函数一般式f(x)=x3+ax2+bx+1 得到三个方程.如何找出三个隐零点之间的关系?通过循环作差得到两个方程,二次作差后三个隐零点关系跃然纸上;法二设出函数的零点式,展开后与一般式对比,运用系数相等,三个隐零点之间的关系显然易见.法二的本质是运用高次函数(方程)的韦达定理,找出根与系数的关系.
题型三、已知零点个数求参数,运用定理去赋值
例3(2017 年全国新课标卷Ⅰ理科第21 题)已知函数f(x)=ae2x+(a-2)ex-x.
(1)讨论f(x)的单调性;
(2)若函数f(x)有两个零点,求a 的取值范围.
思维导引:f(x)的定义域为R,根据函数零点存在性定理,若f(a)f(b)<0,则f(x)在(a,b)内有零点,结合函数单调性,可以确定零点个数.
解析:(1)f(x)的定义域为(-∞,+∞),f ′(x)=2ae2x+(a-2)ex-1=(aex-1)(2ex+1).
若a≤0,则f′(x)<0,所以f(x)在(-∞,+∞)上单调递减.
若a>0,由f ′(x)=0,得x=-lna.当x ∈(-∞,-lna)时,f ′(x)<0;当x∈(-lna,+∞)时,f ′(x)>0.所以f(x)在(-∞,-lna)上单调递减;在(-lna,+∞)上单调递增.
(2)若a≤0,由(1)知,所以f(x)在(-∞,+∞)上单调递减,f(x)至多一个零点,不满足题意.
①当a=1 时,f(-lna)=0,故f(x)仅有一个零点x=0;
②当a>1 时,f(x)min=f(-lna)=1-+lna>0,故f(x)没有一个零点;
③当0<a<1时,f(x)min=f(-lna)=1-+lna<0,而f(-1),故f(x)在(-1,-lna)内有一个零点;

综上所述,当函数f(x)有两个零点时,a∈(0,1).
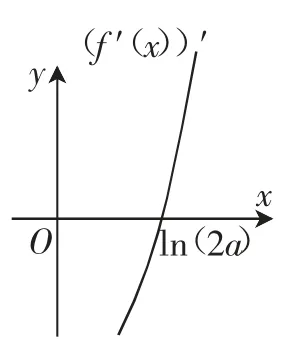
难点破析:如何想到赋值?直接解f(x)=ae2x+(a-2)ex-x>0 显然不现实.函数f(x)的解析式是三个基本初等函数的组合,当x→+∞时,ae2x→+∞2,(a-2)ex→-∞,x→+∞,决定f(x)的符号的关键项为ae2x.在不影响函数f(x)符号的前提下,可利用不等式x≤ex-1 例4(2017 年全国新课标卷Ⅱ理科第21 题)已知函数f(x)=ax2-ax-xlnx,且f(x)≥0. (1)求a; (2)证明:f(x)存在唯一的极大值点x0,且 思维导引:可导函数f(x)存在极值点的必要条件是其对应的导函数f′(x)存在零点x0,不难发现该零点x0是隐零点,想方设法找出x0应该满足的关系. 解析:(1)f(x)=x(ax-a-lnx)≥0⇔ax-a-lnx≥0.设g(x)=ax-a-lnx,则.当a≤0 时,g′(x)<0,g(x)在(0,+∞)上递减,且g(1)=0,则当x≥1 时,g(x)≤0,不符合题意,故a>0.当0<x<时,g′(x)<0,当x>时,g′(x)>0,从而g(x)在上递减,在上递增.所以,又g(1)=0,所以,得a=1. (2)由(1)知f(x)=x2-x-xlnx,则f ′(x)=2x-2-lnx,(f ′(x))′= 难点剖析:函数f(x)的极大值点是其导函数f′(x)=2x-2-lnx 的零点,该零点确实存在,却无法求解出来,不妨设函数f′(x)的隐零点为x0,将f(x0)函数值中的lnx0用2x0-2 整体代换,同时注意确定x0的合适范围:,这样逐层转化、抽丝剥茧,问题便迎刃而解. 例5(2018 年全国新课标卷Ⅱ理科第21 题)已知函数f(x)=ex-ax2. (1)略; (2)若f(x)在(0,+∞)上只有一个零点,求实数a. 思维导引:f(0)=1>0,又易见x→+∞时,f(x)>0,f(x)在(0,+∞)上只有一个零点,即要求f(x)的极小值为0. 解析:当a≤0 时,因为x∈(0,+∞)时f′(x)=ex-2ax>0,所以f(x)在(0,+∞)上为增函数.又f(0)=1>0,所以f(x)在(0,+∞)上没有零点. 当a>0 时,令f′(x)=ex-2ax,(f′(x))′=ex-2a. 图1 图2 图3 难点剖析:a>0 时,对可导函数f(x)来说,可以通过原函数的二阶导数的符号,研究其一阶导数的单调性,通过一阶导数的符号,研究原函数的单调性.原函数的唯一零点就是其极小值点. 综上所述,隐零点问题出现的背景形式多样,灵活多变,与隐零点有关的试题已经逐渐成为模拟试题乃至高考真题中的热点、流行色,久考不衰,应引起我们教师的重视!当然对于以上各类问题,笔者仅仅从隐零点角度去剖析、甄别,至于其他角度,这里就不再一一赘述.题型四、抽丝剥茧隐零点,设而不求代整体
题型五:借助函数单调性,刻画零点的性质