数学解题也需“以退求进”

☉江苏省宜兴中学 郭骏聪

数学解题，必须讲究策略，有退有进.所谓进，即按照题意步步深入，这对较为简单的题目十分有效，但当你碰到较为复杂的问题时，只想到进可能就会无门可入，这时就要想到退，可谓“退一步，海阔天空”，退回定义、退回原始问题、退回简单问题，只要把最简单的问题想通想透，原来的问题就会迎刃而解.“以退求进”是一种好的解题方法，那么究竟怎么“退”呢？

一、从结论向条件“退”

由结论出发，反推命题成立的条件，这其实就是推理与证明中的分析法.在不等式证明中应用最为广泛.

例1设a＞b＞0，求证

分析：直接证明结论非常困难，故可从结论入手，寻找使结论成立的充分条件，即采取分析法证明.

点评：对于不等式的证明一般先采用分析法探求思路，再用综合法书写.如果当用分析法反推时每一个步骤都是等价的，这时也可以采用分析法书写，但一定要注意书写的规范性.

二、从一般向特殊“退”

一般与特殊既是一对矛盾体，又是一对统一体.从特殊到一般，这是人们认识事物并掌握事物发展规律的一般方法，体现了辩证唯物主义矛盾论的观点.数学解题也是如此.我们要解决一个一般的问题时，可以从特殊入手，即所谓的特殊值法，从中找出规律，并用一般的方法加以验证，这种方法对于某些证明题十分有效.

例2已知方程x2+y2+2（2-cos2θ）x-2（1+sin2θ）y-4cos2θ+2sin2θ+5=0，试证明：无论θ 取何实数值，该方程所表示的曲线总是经过两个定点P1和P2，并求定点P1和P2的坐标.

分析：已知方程本质上是圆系方程，θ 可取特殊值0，得

证明：当x=-1，y=2 时，

x2+y2+2（2-cos2θ）x-2（1+sin2θ）y-4cos2θ+2sin2θ+5

=5-2（2-cos2θ）-4（1+sin2θ）-4cos2θ+2sin2θ+5

=5-4+2cos2θ-4-4sin2θ-4cos2θ+2sin2θ+5

=2-2（cos2θ+sin2θ）=2-2=0.

当x=-2，y=1 时，同理可得：

x2+y2+2（2-cos2θ）x-2（1+sin2θ）y-4cos2θ+2sin2θ+5=0.

故无论θ 取何实数值，方程所表示的曲线总经过两个定点P1（-1，2），P2（-2，1）.

点评：对于定点、定值问题，一般可采用特殊化法，找到定值或定点，然后加以验证.

三、从抽象向具体“退”

数学是从实际问题中抽象出来的，因此解题时可将数学的抽象性退回到实际问题的“具体性”，从而更能把握住问题的本质.

例3已知集合A 和集合B 分别有12 个元素，A∩B 中有4 个元素，请求出同时满足以下两个条件的集合C的个数：①CA∪B，并且C中必须含有3个元素；②C∩A≠Ø.

分析：题意比较抽象，导致理解较困难，所以可将原问题退到一个实际问题，选择具体的模型来将原题的意思表达出来.

解：假设我班英语兴趣小组与体育兴趣小组分别有12 人（集合A 与B），其中有4 名学生同时参加了两个兴趣小组（A∩B），现从这些学生中挑选3 人（集合C），来参加一次兴趣小组组织的活动，要求至少有1 人是英语小组成员，问：这样的组团方式有多少种？问题的实质未发生任何变化，但求解思路十分明晰，所以可直接写出结果如下：

点评：从抽象向具体“退”，就是建立相关的数学模型，体现了数学解题的构造思想.由数思形，挖掘所求问题的几何意义或实际意义，是从抽象向具体“退”最常见的思维方法.

四、从高维向低维“退”

在几何问题中，将立体几何问题“退”成平面几何来求解，这种从“三维空间”退到“二维平面”上来解的方法，体现了复杂问题简单化的解题策略.

例4求证：在四面体中连接顶点与对面重心的四条线相交于一点，且此点将每一线段分成3∶1.

分析：从三维向二维后退，让我们先证明一个相类似的平面几何题：三角形三条中线交于一点，并且此点把每一条中线都分成2∶1 两个部分.

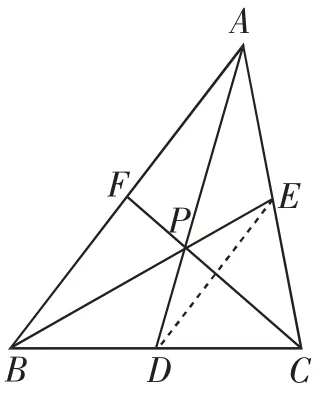
图1

证明：如图1，设中线BE，AD交于点P，连接DE，则DE∥AB且.连接CP 并延长交AB 于F，则△DEP∽△ABP，故.所以中线EB，AD 交于一点，此点分AD 为2∶1，同理可证CF 与中线AD 交于一点，此点分AD 为2∶1，所以两个交点是同一点，即AD，BE，CF 交于同一点P，且点P 分AD，BE，CF都为2∶1.

下面给出例4 的证明：

证明：设四面体A-BCD的表面BCD的重心为G1，表面ACD的重心为G2，表面ABD 的重心为G3，表面ABC 的重心为G4，取线段CD的中点M，连接AM 和BM，则G1，G2分别在BM，AM 上，且AG2∶G2M=BG1∶G1M=2∶1，连接AG1，BG2交于点O，又连接G1G2.

因为AG2∶G2M=BG1∶G1M=2∶1，所以G1G2∥AB.

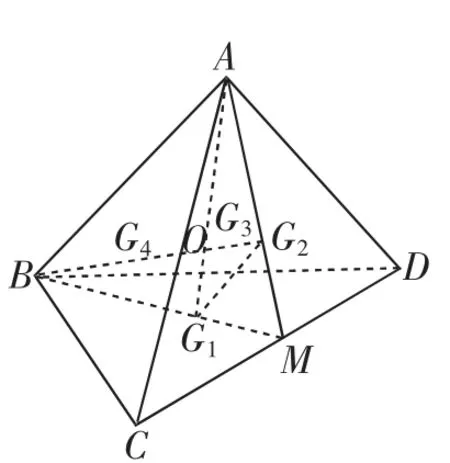
图2

所以AB∶G1G2=AM∶G2M=3∶1，易证△OG1G2∽△OAB.

所以AO∶OG1=BO∶OG2=AB∶G1G2=3∶1.

同理可得：线段CG3与线段AG1相交于一点，并且此点分线段AG1为3∶1，线段DG4与线段AG1相交于一点，并且此点分线段AG1为3∶1，因此，AG1，BG2，CG3，DG4相交于一点O，且点O 分AG1，BG2，CG3，DG4都为3∶1.

点评：立体几何的证明方法或策略，可以由相应的平面几何问题的求解方法中类比获得，体现了数学解题的类比思想.

五、从综合向单一“后退”

综合题，是考试的重点题型，主要考查考生的综合能力.任何复杂问题都是由简单问题组合起来的，面对综合性问题，我们可将其“瓦解”成几个单一问题.

例5设函数f（x）是奇函数，对于任意x，y∈R 都有f（x+y）=f（x）+f（y），且x＞0 时，f（x）＜0，f（1）=-2.试问：当-3≤x≤3 时，f（x）有最值吗？若有，求出最值；若没有，试说明理由.

分析：对于函数综合题，一般可把整个大问题分解，变成若干个小问题来解.

解：（首先来判断单调性）设x1，x2∈R，且x1＜x2，则x2-x1＞0.

由题意可得f（x2-x1）＜0，而f（x2-x1）=f（x2）+f（-x1），又因为f（x）是奇函数，故f（x2）+f（-x1）=f（x2）-f（x1）＜0，即f（x1）＞f（x2）.故f（x）在实数集上是单调递减函数.

（下面求f（3）的值）因为f（1）=-2，并且对于任何实数x，y，均有f（x+y）=f（x）+f（y）成立，故f（2）=f（1）+f（1）=-4，f（3）=f（2）+f（1）=-6.

又由于f（x）是奇函数，所以f（-3）=-f（3）=6.

综上可知，当-3≤x≤3时，f（x）有最值，且最大值为f（-3）=6，最小值为f（3）=-6.

点评：本题是最常见的抽象函数的性质证明及应用问题，解答这类综合性问题需采用“化整为零，各个击破”的策略.

自古兵法有“欲擒故纵”，而数学解题有“以退求进”，两者其实是一个道理.