一道双曲线考题的多解探究
☉福建省莆田第六中学 祁国伟
本文拟通过对一道双曲线考题的多解探究,旨在激发同学们的探究意识,拓宽解题思维,强化双曲线与其他知识的综合运用能力,以便帮助同学们理清常用解题思路,进一步提高分析、解决此类问题的能力.
【考题再现】(2019 年全国Ⅰ卷第16 题)已知双曲线的左、右焦点分别为F1、F2,过F1的直线与C的两条渐近线分别交于A,B两点.若,则C 的离心率为______.
多解探究:如图1,先画出适合题意的图形,因为,所以A 为F1B 的中点.又O 为F1F2的中点,所以OA 是△BF1F2的中位线.所以OA∥F2B.又由得F1B⊥F2B,所以可得F1B⊥OA.
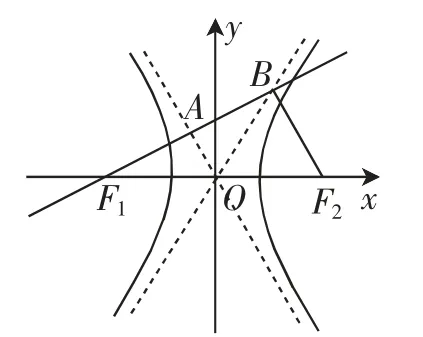
图1
解法一:因为点F1(-c,0)到直线的距离,又|OF1|=c,所以
答案:2.
解法二:同解法一先求得|AF1|=b,|OA|=a.于是,直线BF1的方程为,又直线OB 的方程为,所以联立可求得点B 的纵坐标为
因为易知|BF1|=2b,|BF2|=2a,|F1F2|=2c,所以Rt△BF1F2斜边上的高为
答案:2.
解法三:因为点B 在渐近线上,所以可设点.又F1(-c,0),A 为F1B 的中点,所以点A 的坐标为
接下来,给出三种不同的思路.
思路1:因为点,又点F1(-c,0)到直线的距离=b.所以两边平方得,整理得c4-8a2c2+16a4=0,两边同除以a4得e4-8e2+16=0,即(e2-4)2=0,所以e2=4.
答案:2.
思路2:因为点,所以.所以由,得,化简得所以
答案:2.
思路3:因为点,所以由AF1⊥OA 得kAF1·kAO=-1,即,化简得所以c=
答案:2.
解法四:因为A 为F1B 的中点,又F1B⊥OA,所以OA 是线段F1B 的中垂线.所以∠F1OA=∠AOB.
又由直线OA,OB 是双曲线的渐近线可得∠F1OA=∠BOF2,所以∠F1OA=∠AOB=∠BOF2.
又∠F1OA+∠AOB+∠BOF2=π,所以
接下来,给出两种不同的思路.
思路1:由直线OA 的方程是可得=tan ∠AOF2=,所以.所以c=
答案:2.
思路2:同解法一可求得|AF1|=b,|OA|=a.
于 是,在Rt △F1AO 中,由cos ∠F1OA=,可得,化简得c=2a.
答案:2.
解法五:因为,所以点B 在以F1F2为直径的圆x2+y2=c2上.
又A 为F1B 的中点,所以点A 的坐标为
答案:2.
评注:上述解法一、二、三侧重于从“数”的角度加以研究,显得整个解题过程烦琐一些,运算量较大;解法四侧重于从“形”的角度加以研究,充分借助平面几何知识及渐近线的图形特征探究获得是整个求解的关键所在;解法五以构造圆为切入点,关键是准确求解点B 的坐标,并充分利用点A 的几何特征(既是线段F1B 的中点,也在渐近线上).对比可知,解法四、五比较简单,可称之为“秒杀”法!
以上,呈现了求解双曲线离心率的五种不同解题方法,它们各有自己的优势与局限.显然,多解探究沟通了双曲线与平面向量、平面几何、直线及圆等知识的内在联系,优化了考生的认知结构,培养了考生的探究、创新意识,进一步提升了考生的直观想象、数学运算等核心素养.一言以蔽之,该题设计较好,有利于各类考生充分发挥各自的思维优势与数学潜能,是一道难得的可以有效培养数学思维的好题.

