螺栓超欠拧对钢桁梁桥节点拼接接头受力的影响

高强，黄天立，陈龙，冯锡良

(1.中南大学土木工程学院，湖南长沙，410075；2.中国中铁二局集团有限公司，四川成都，610031)

钢桁梁具有构造简单、强度高、自身质量小、施工速度快等优点，被广泛应用于桥梁建设。20世纪90年代，我国第1 次采用焊接整体节点和节点外拼接技术建成京九线孙口黄河大桥，随后建成的芜湖长江大桥、四渡河大桥、东新赣江特大桥、郑新黄河大桥等均采用了这种施工工艺。焊接整体节点技术将节点板与一端的弦杆焊接成为一个整体，节点外拼接技术即主桁杆件与焊接整体节点在节点外通过高强螺栓连成一体。但在实际施工过程中，受扭矩扳手精准度、螺栓质量的离散型、人为操作误差或疏忽等影响，螺栓的真实预紧力可能达不到安装要求，这势必对节点拼接接头各板件的受力产生影响。施刚等[1]对高强螺栓连接进行了研究。党志杰[2-3]通过理论分析并结合试验研究，提出了一种计算高强螺栓应力集中系数及接头螺栓传力比的方法，以及摩擦型高强螺栓接头极限滑移荷载的判断标准。张晔芝等[4]对摩擦型高强螺栓接头的受力机理和极限状态进行了试验研究，通过非线性有限元分析研究了荷载水平、螺栓排数和螺栓间距等因素对头排螺栓传力比的影响。陈成军等[5]研究了预紧顺序和初始预紧力对螺栓组连接过程弹性相互作用的影响规律。HUANG 等[6]对高强螺栓连接接头的传力特性进行了有限元模拟与试验研究。GUO等[7]对咬合式高强螺栓连接的抗剪承载力进行了试验研究和数值模拟。张德莹等[8]对高强螺栓连接的传力性能及螺栓缺失的影响进行了相关研究。朱铭等[9]对钢桁桥长列高强螺栓群优选布置问题进行了有限元分析。周焕廷等[10]基于ANSYS 软件数值模拟研究了高强螺栓连接的极限承载能力和变形性能。徐海鹰[11]通过模型试验、接触单元有限元计算和理论分析，对摩擦型多排高强度螺栓连接的传力性能、接头折减系数和极限状态进行了研究。沈国辉等[12]通过对螺栓节点板抗剪连接的有限元模拟方法进行研究，发现在板件间设置接触约束并对螺栓杆施加预紧力作用是最合理的一种方法。KIM等[13-17]采用该方法对高强螺栓连接进行了相关研究。MOŽE等[18-19]制作了若干组单螺栓连接和双螺栓连接试件，通过试验和数值分析研究了不同端距、边距及螺栓间距对钢板在栓孔处承压性能及破坏形式的影响。结果表明，钢板在栓孔处的承压承载力与端距及螺栓间距呈线性关系，而与垂直于受力方向的边距基本没有关系。GUO 等[20]制作了20 组Q460D 高强钢螺栓连接接头，通过试验和数值分析，研究了不同端距、边距及螺栓间距对连接承载能力及变形的影响，发现螺栓横向布置时，Q460D 高强钢试件的承载力和变形随着螺距增大而增大；而对于端距及边距，当达到标准值之后，继续增大其值对连接承载力的影响很小。当螺栓纵向排列时，试件承载力只随着螺距增大呈现线性增大的趋势。ELLIOTT 等[21]研究了钢结构螺栓连接的性能，发现使用与螺栓直径相对应的剪切破坏面大大高估了对具有较小或无孔间隙的螺栓连接的极限承载力，而对于标准、超大尺寸或无间隙螺栓孔的试件，使用有效剪切面是准确的。目前关于高强螺栓连接的研究工作主要侧重于其传力特性及承载能力，而针对高强螺栓超欠拧对接头板件受力影响的研究较少。为此，本文作者以浩吉铁路(原蒙西—华中地区铁路)跨平汝高速64 m 钢桁梁桥为工程背景，建立E4节点的实体有限元模型。在E4节点处，选取下弦顶板上的一组螺栓作为超欠拧对象，并以该组螺栓不同的施拧状态作为研究工况，研究不同工况状态下接头各板件的应力状态，并进行现场试验验证，最后得出螺栓超欠拧对接头各板件应力状态的影响规律。

1 工程背景

浩吉铁路(原蒙西—华中地区铁路)跨平汝高速大桥全长210.705 m，设置5 墩2 台，桥跨由1 片24 m 简支T 梁+1 榀64 m 钢 桁梁+1 片32 m 简 支T梁+3片24 m简支T梁组成。线路在1号和2号墩之间跨平汝高速设计为1 榀64 m 钢桁梁。钢桁梁为单线整体节点平行弦三角桁架下承式简支钢桁梁，计算跨度为64 m，梁全长为66 m，其中两端支座中心线梁端距离1 m，节间长度为12.8 m，桁高12.8 m，主桁中心距为8.5 m。主桁杆件与整体节点通过高强螺栓连接而成，板件材料均采用Q370qD 钢材，高强螺栓采用10.9S M24 规格，材质为35VB，螺母及垫片均采用45号优质碳素结构钢，螺栓孔直径为26 mm。钢桁梁结构示意如图1所示。

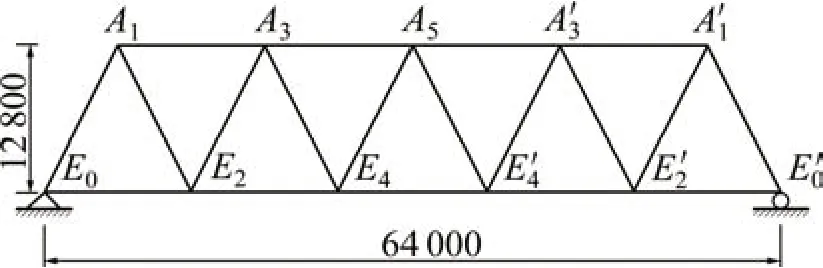
图1 钢桁梁结构示意图Fig.1 Sketch of steel truss girder bridge

2 有限元建模计算

分别采用有限元软件MIDAS/CIVIL和ANSYS建立跨平汝高速大桥全桥有限元模型和E4节点的实体有限元模型，全桥有限元模型的计算结果为E4节点模型提供受力边界条件。

2.1 全桥有限元建模计算

跨平汝高速大桥钢桁梁采用现场拼装完成后整体拖拉施工。采用有限元分析软件MIDAS/CIVIL建立全桥模型，如图2所示，钢桁梁杆件均采用梁单元模拟。通过全桥有限元计算分析得出E4节点受力最不利施工状态，其对应的全桥临时支撑情况如图3所示。

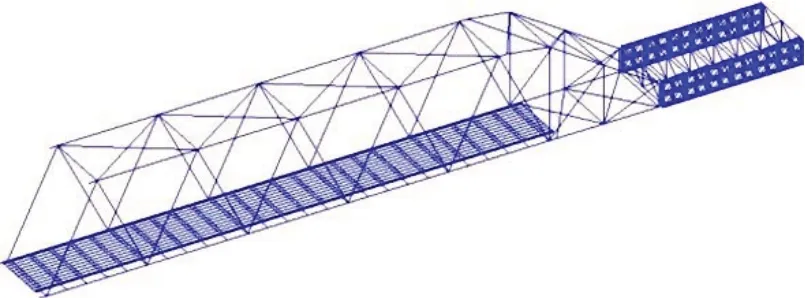
图2 全桥有限元模型Fig.2 Finite element model of bridge

2.2 E4节点有限元建模计算

图4所示为E4节点的受力示意图。在节点E2E4端施加固定束，通过全桥有限元计算分析，得到E4节点在最不利状态下的受力边界条件，如表1所示(支反力为1 821.00 kN)。

图3 E4节点受力最不利状态下全桥临时支撑示意图Fig.3 Diagram of temporary support for bridge under the most unfavorable condition ofE4 joint

图4 E4节点受力示意图Fig.4 Sketch of mechanical state ofE4 joint

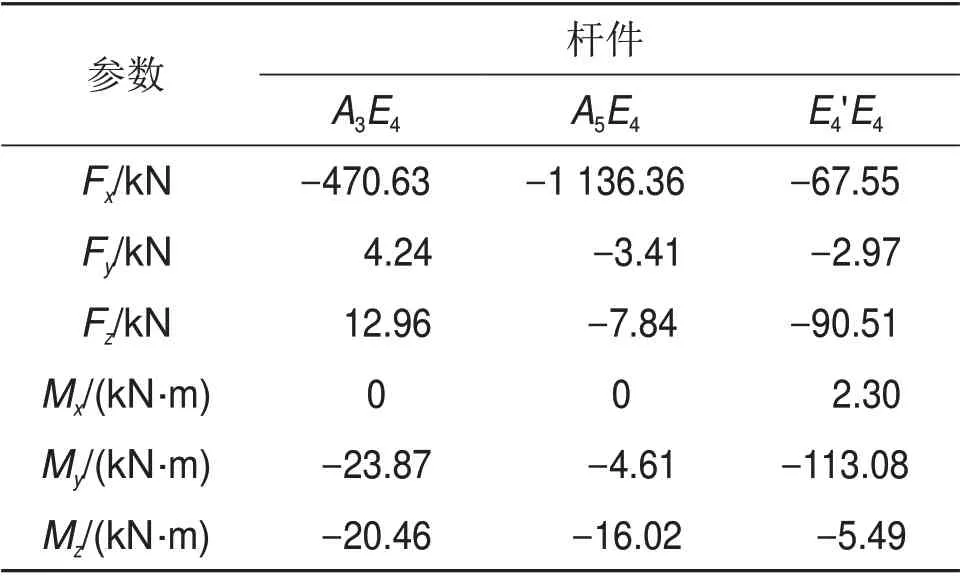
表1 E4节点边界条件Table 1 Boundary conditions ofE4 joint

图5所示为采用ANSYS 有限元软件建立的E4节点实体有限元模型，模型中各构件采用solid186六面体实体单元并辅以solid187 四面体实体单元，构件间接触采用conta174和targe170单元模拟，采用螺栓预紧功能对螺栓施加预紧力[12]。图6所示为E4节点模型的拼接接头子模型，由拼接板、下弦顶板及螺栓群组成。本文主要以该子模型为研究对象，选取螺栓L1和L2为超欠拧对象，并以该组螺栓不同的施拧状态作为研究工况，见表2。然后，对拼接板及下弦顶板在不同工况状态下的应力状态进行计算分析。

图5 E4节点有限元模型Fig.5 Finite element model ofE4 joint

表2 螺栓超欠拧工况Table 2 Over-under-tightening conditions of bolts

为了更直观地分析不同超欠拧工况状态下拼接板及下弦顶板的应力分布情况，在计算模型上定义10 条应力分析路径K1～K10，应力路径布置如图7和图8所示。

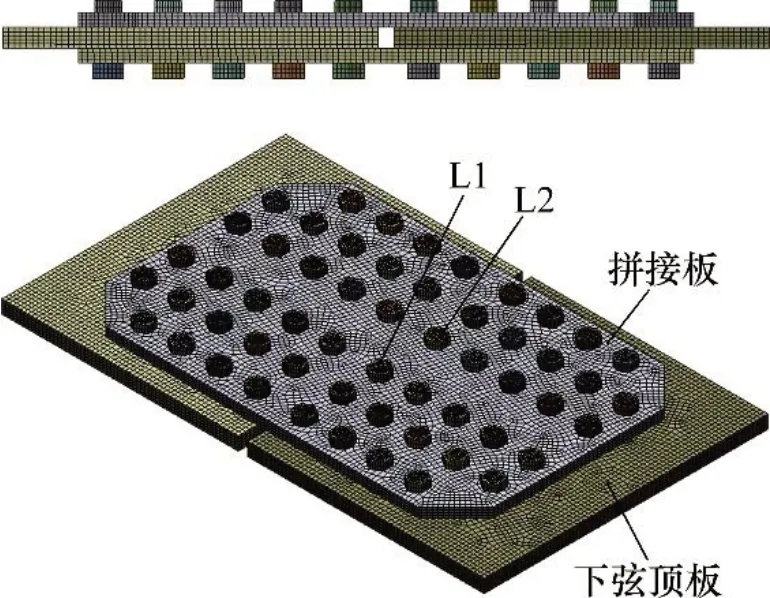
图6 拼接接头子模型Fig.6 Submodel of connection

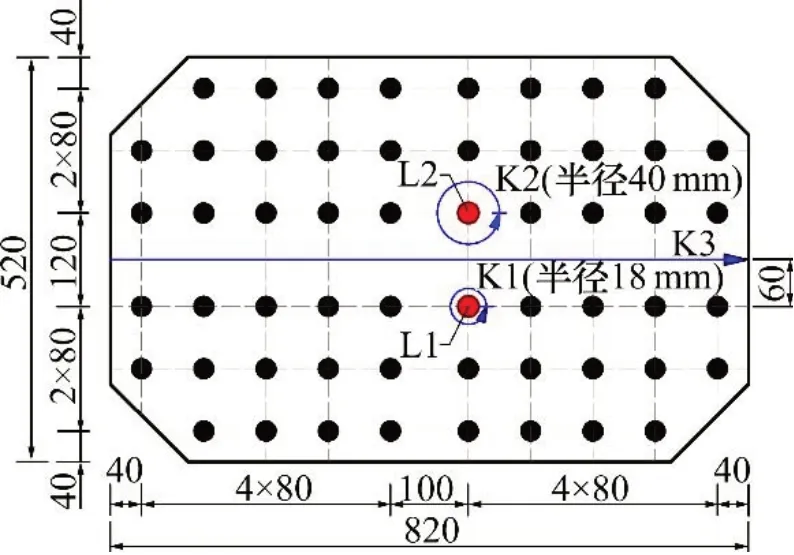
图7 拼接板应力路径布置Fig.7 Layout of stress paths of lap plate

图8 下弦顶板应力路径布置Fig.8 Layout of stress paths of bottom chord roof

3 计算结果分析

3.1 拼接板应力分析

图9所示为拼接板Von-Mises 等效应力云图，其中，图9(a)至9(f)所示分别为拼接板在螺栓L1和L2 漏拧、欠拧50%、欠拧25%、正常预紧、超拧10%以及超拧20%工况状态下的Von-Mises等效应力云图。由图9可知：

1) 拼接板等效应力沿板轴向呈波浪形分布，在螺栓中心连线上应力较大，在螺栓行间应力较小。

2)随着螺栓L1和L2的预紧力增大，拼接板在L1 和L2 附近区域的应力增大很明显，而距离L1和L2较远区域的应力没有明显变化。

在不同工况状态下，拼接板在K1 和K2 路径上的Von-Mises等效应力分别如图10和图11所示，其中，K1路径的环形半径为18 mm，K2路径的环形半径为40 mm，0刻度均对应路径起点。由图10和图11可知：

1) 随着螺栓L1 和L2 预紧力增大，拼接板在K1 和K2 路径上的应力均明显增大，这表明在L1和L2 附近区域，其应力随L1 和L2 预紧力增大而增大。

2) 对比K1 和K2 路径上的应力在不同工况状态下的变化情况，对于K1路径，从漏拧工况到超拧20%工况的应力在54.7～171.2 MPa 之间变化，而K2路径对应的应力在21.6～52.6 MPa之间变化。由此可知，在L1 和L2 附近区域，离L1 和L2 越近，应力受L1和L2施拧状态的影响越大。

图12所示为不同工况状态下拼接板在K3路径上的Von-Mises 等效应力对比结果，K3 路径的长度为820 mm，0刻度对应路径起点。

由图12可知：随着螺栓L1 和L2 的预紧力增大，拼接板在K3 路径上的应力只在L1 和L2 附近区域有明显增大，且离L1和L2越近的点，其应力受L1 和L2 施拧状态的影响越大，离L1 和L2 越远的点，其应力受L1和L2施拧状态的影响越小。从图12还可看出：拼接板应力受L1 和L2 施拧状态影响的范围为以L1(L2)为中心1.4 倍螺栓中心距之内。

3.2 下弦顶板应力分析

图13所示为下弦顶板Von-Mises 等效应力云图，其中，图13(a)至图13(f)所示分别为下弦顶板在螺栓L1和L2漏拧、欠拧50%、欠拧25%、正常预紧、超拧10%以及超拧20%工况状态下的Von-Mises等效应力云图。由图13可知：

1)下弦顶板等效应力沿板轴向呈波浪形分布，在螺栓中心连线上应力较大，在螺栓行间应力较小。

2)随着螺栓L1和L2的预紧力增大，下弦顶板在L1 和L2 附近区域的应力增大很明显，而离L1和L2较远区域的应力没有明显变化。

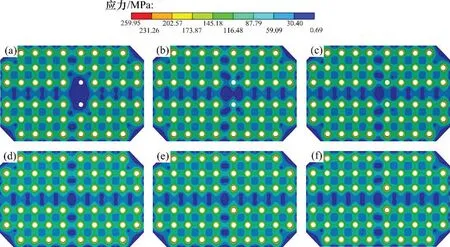
图9 各工况状态下拼接板等效应力云图Fig.9 Nephograms of equivalent stresses of lap plate under different conditions

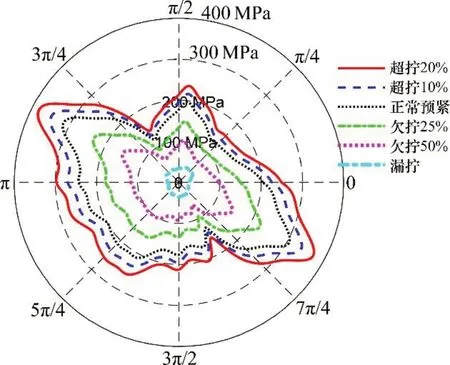
图10 各工况状态下K1路径等效应力对比Fig.10 Comparison of equivalent stresses of K1 path under different conditions

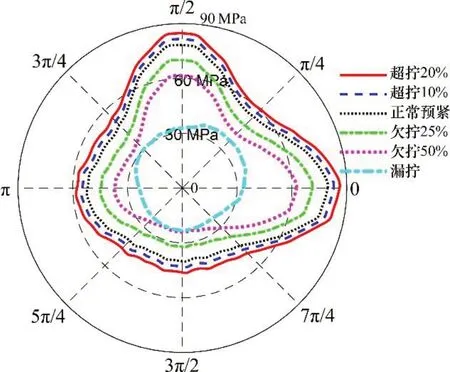
图11 各工况状态下K2路径等效应力对比Fig.11 Comparison of equivalent stresses of K2 path under different conditions

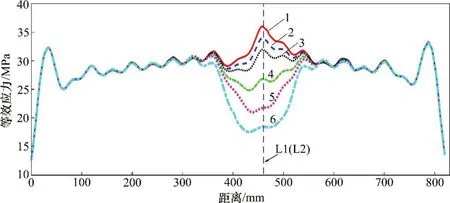
图12 各工况状态下K3路径等效应力对比Fig.12 Comparison of equivalent stresses of K3 path under different conditions

图13 各工况状态下下弦顶板等效应力云图Fig.13 Nephograms of equivalent stresses of bottom chord roof under different conditions

图14所示为不同工况状态下下弦顶板在K4至K6路径上的Von-Mises等效应力对比图。K4，K5和K6 路径的长度皆为600 mm，K4，K5 和K6 路径距下弦顶板端部的距离分别为55，80 和160 mm，0刻度均对应路径起点。

由图14(a)可知：随着螺栓L1 和L2 的预紧力增大，下弦顶板在K4路径上的应力只在螺栓L1和L2附近区域有明显增大，且离L1和L2越近的点，其应力受螺栓L1和L2施拧状态的影响越大，离螺栓L1 和L2 越远的点，其应力受螺栓L1 和L2 施拧状态的影响越小。从图14(a)可以看出：下弦顶板应力受螺栓L1 和L2 施拧状态影响的范围为以L1(L2)为中心0.8倍螺栓中心距之内。

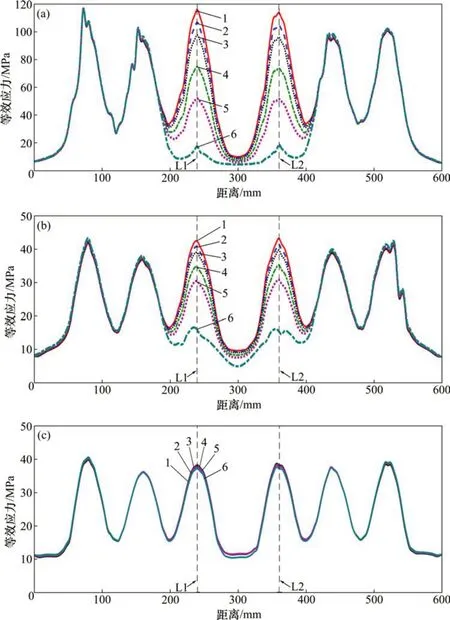
图14 各工况状态下下弦顶板等效应力对比Fig.14 Comparison of equivalent stresses of bottom chord roof under different conditions

由图14(b)可知：随着螺栓L1 和L2 的预紧力增大，下弦顶板在K5路径上的应力只在螺栓L1和L2 附近的区域有明显增大，且离螺栓L1 和L2 越近的点，其应力受L1 和L2 施拧状态的影响越大，离L1 和L2 越远的点，其应力受螺栓L1 和L2 施拧状态的影响越小。从图14(b)可以看出：下弦顶板应力受螺栓L1 和L2 施拧状态影响的范围为以L1(L2)为中心0.8倍螺栓中心距之内。

对比图14(a)与图14(b)可知：对于K4 路径，从漏拧工况到超拧20%工况，其应力变化最大值为98.5 MPa，而K5 路径对应的应力变化最大值为27.9 MPa。这是由于K5路径相对K4路径而言距离螺栓L1 和L2 更远，因此，K5 路径上的应力相对K4路径而言受L1和L2施拧状态的影响更小。

由图14(c)可以看出：在螺栓L1 和L2 不同的施拧状态下，下弦顶板在K6路径上的应力几乎没有发生变化。这主要是因为K6 路径相对K4 和K5路径而言距离螺栓L1和L2太远，其路径上的点超出了受L1和L2施拧状态影响的范围。

3.3 接触面摩擦应力分析

图15(a)～(f)所示分别为接触面在螺栓L1和L2漏拧、欠拧50%、欠拧25%、正常预紧、超拧10%以及超拧20%工况状态下的摩擦应力云图。由图15可知：

1)拼接板与下弦顶板接触面摩擦应力沿螺栓孔向周围环状递减。

2) 随着螺栓L1 和L2 的预紧力增大，螺栓L1和L2 周围的摩擦应力增大很明显，而其他螺栓周围的摩擦应力没有明显变化。

图16(a)～(d)所示分别为不同工况状态下接触面在K7，K8，K9和K10路径上的摩擦应力对比结果。K7～K10路径的环形半径均为15 mm，0刻度均对应路径起点。其中，K7 对应螺栓L2，K8～K10分别对应L2右侧的不同螺栓，如图8所示。

由图16(a)可以看出：随着螺栓L1 和L2 的预紧力降低，拼接板与下弦顶板接触面在K7路径上的摩擦应力也随之减小。由图16(b)和图16(c)可以看出：随着螺栓L1和L2的预紧力降低，拼接板与下弦顶板接触面在K8 和K9 路径上的摩擦应力整体上有不同程度增大。而对比图16(b)和图16(c)可知：K9路径上的摩擦应力增大的幅度要比K8路径的小，这是由于K9 对应的螺栓比K8 对应的螺栓离L1 和L2 更远。从图16(d)可以看出：随着螺栓L1和L2的预紧力降低，拼接板与下弦顶板接触面在K10 路径上的摩擦应力基本没受影响，这是由于K10对应的螺栓离L1和L2太远。

分析图16可知：从超拧20%工况到漏拧工况，随着螺栓L1 和L2 的预紧力降低，由螺栓L1 和L2所产生的接触面摩擦应力也随之降低，从而导致螺栓L1 和L2 的传力减小，而在螺栓L1 和L2 周围的其他螺栓的传力将不同程度地增大，且距离螺栓L1和L2越近的螺栓，其传力增大幅度越大，距离螺栓L1 和L2 越远的螺栓，其传力增大幅度越小。这说明螺栓超欠拧会对板件间的摩擦传力产生影响。

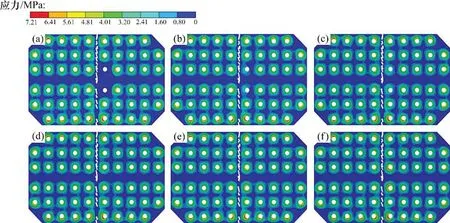
图15 各工况状态下接触面摩擦应力云图Fig.15 Nephogram of friction stresses of the contact surface under different conditions

图16 各工况状态下接触面摩擦应力对比Fig.16 Comparison of friction stresses of the contact surface under different conditions

4 试验验证

为了对有限元分析结果进行试验验证，在拼接板K3 路径上布置10 个应力测点进行现场试验，具体布置如图17所示。应力测点均使用三轴45°应变花测量，采用DH3816N 静态应力应变测试分析系统采集测点应力。

图18所示为各工况状态下K3路径应力计算值与试验值[22]对比结果。从图18可以看出：应力计算值与试验值基本相同，应力变化趋势基本一致。由此可知，本文的有限元计算分析结果与工程实际结果是相符的。

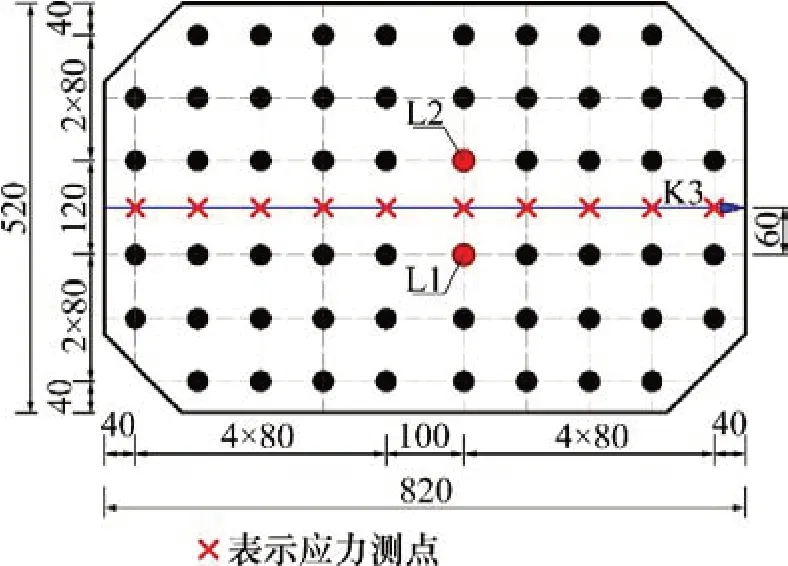
图17 应力测点布置Fig.17 Layout of test point of stresses

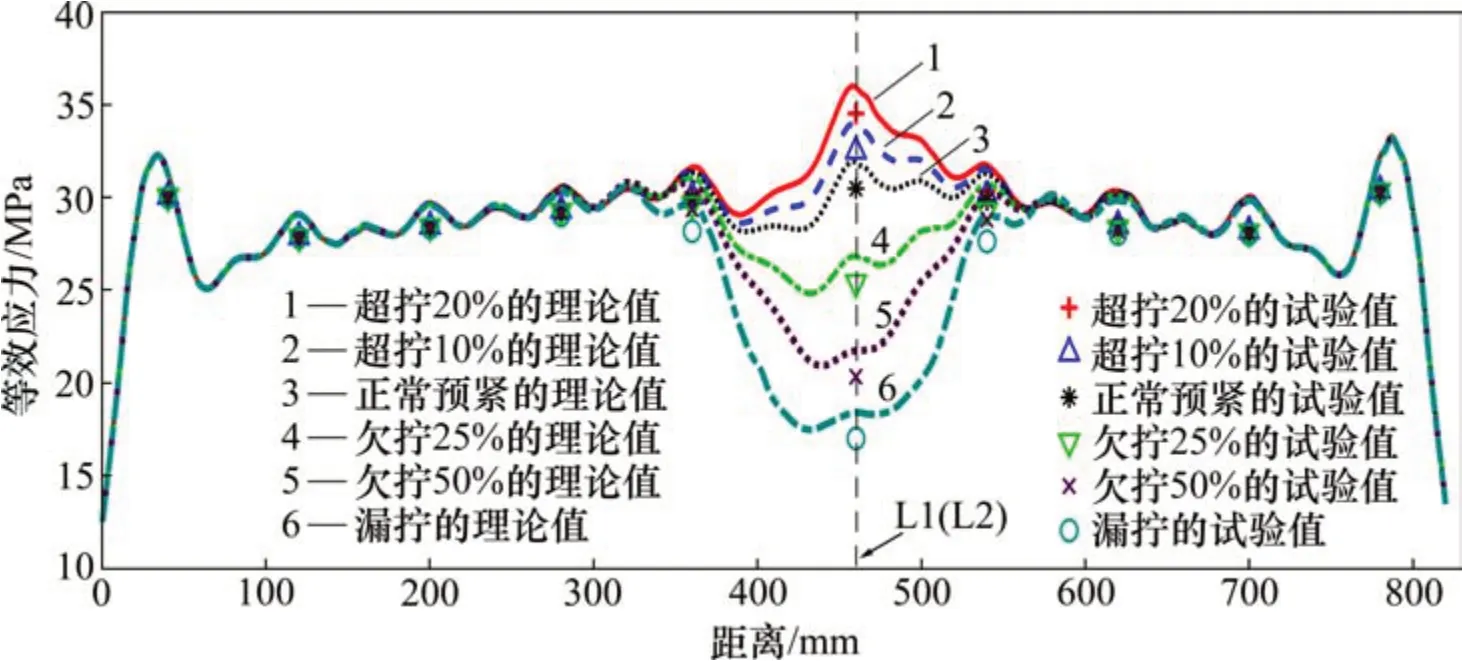
图18 各工况状态下K3路径应力计算值与试验值对比Fig.18 Comparison of the calculated stress and tested stress of K3 path under different conditions

5 结论

1)当某一螺栓发生超欠拧时，只会对该螺栓附近一定区域的板件应力产生影响，并且离该螺栓越近影响越大，离得越远影响越小。

2)螺栓超欠拧对拼接板应力的影响范围为以超欠拧螺栓为中心1.4倍螺栓中心距之内，对下弦顶板应力的影响范围为以超欠拧螺栓为中心0.8倍螺栓中心距之内。

3)螺栓超欠拧会对板件间的摩擦传力产生影响。当某一螺栓发生超欠拧时，随着该螺栓预紧力降低，由该螺栓所产生的接触面摩擦应力也随之降低，从而导致该螺栓的传力减小。而在该螺栓周围其他螺栓的传力将不同程度地增大，并且距离该螺栓越近的螺栓，其传力增大幅度越大，距离该螺栓越远的螺栓，其传力增大幅度越小。