局部剥落故障对滚动轴承接触与振动特性的影响

刘静，唐昌柯，师志峰，王林峰，徐子旦，邵毅敏

(1.重庆大学 机械传动国家重点实验室，重庆，400044；2.重庆大学机械工程学院，重庆，400044)

滚动轴承是重要基础部件之一，广泛应用于工业、能源和航天等行业的关键机械装备。滚动轴承的运行状态和寿命直接影响机械装备的运转状态，30%的旋转机械故障是由轴承故障引起的[1-3]。滚动轴承的故障形式包括锈蚀、断裂、磨损、疲劳剥落和胶合等，许多研究者对滚动轴承滚道表面的局部剥落故障进行研究。当滚动轴承出现局部剥落故障时，会导致轴承刚度发生变化，使得轴承的振动水平增大[4-5]，甚至危害整套机械装备。因此，需要深入研究局部剥落故障诱发的滚动轴承振动特征。对滚子与局部剥落故障周围区域接触特性的深入认识将有助于理解轴承局部剥落故障的振动特征，为轴承的故障诊断和振动特征识别提供有益的参考。针对滚动轴承部件局部剥落故障与滚子的接触特性问题，许多学者进行了大量研究工作。BRANCH等[6]利用试验和有限元的方法，研究了球轴承滚动体冲击剥落故障边缘时引起的临界应力和塑性应变。PATIL 等[7]建立了带有局部剥落故障的球轴承动力学模型，研究了局部剥落故障尺寸对轴承振动特征的影响规律。牛蔺楷等[8]以刚体动力学碰撞理论为基础，在分析滚动轴承运动学特性的基础上，对滚动体通过局部剥落故障时产生的冲击力进行了分析和计算。樊莉等[9]运用ANSYS/LS-DYNA软件，建立了含局部剥落故障的滚动轴承有限元模型，研究了局部剥落故障对轴承滚动体与滚道之间接触应力的影响规律。张福星等[10]利用有限元方法，分析了深沟球轴承滚动体和内、外圈不同部位接触应力和变形的分布。张雪等[11]通过计算轴承接触表面及次表面应力等证明了有限元分析的正确性。伍济钢等[12]将轴承的表面损伤故障考虑为冲击函数分别加载到轴承的内外圈及滚动体上，计算了轴承振动和频谱分析。剡昌锋等[13]计算了考虑弹流润滑及滑动作用下滚动轴承系统局部缺陷位移激励的动力学响应。尽管上述研究采用集中质量法和有限元分析方法讨论了局部剥落故障过渡区对滚子与滚道之间接触应力及其诱发的振动特征，但是缺乏滚子通过轴承局部缺陷故障时滚子与滚道之间接触特性的相关研究。针对上述问题，本文作者采用有限元分析方法，建立圆柱滚子轴承滚子与滚道接触二维有限元等效模型，分析单个滚子进入和退出滚道局部剥落故障区域的过程中滚子与滚道之间的接触特性。研究局部剥落故障宽度对滚子与滚道之间的接触区宽度、接触变形、接触应力分布状态与接触刚度的影响规律，讨论局部剥落故障过渡区对轴承振动特性的影响规律，为深入认识局部剥落故障诱发的滚动轴承的振动特征提供参考。

1 模型描述

1.1 圆柱滚子与滚道等效接触模型

图1所示为局部剥落故障出现时圆柱滚子通过局部剥落故障区域的过程。图1中：Q为作用于滚子上的径向载荷；v为滚子运动方向；O1和O2分别为滚子在通过局部剥落故障过程中的不同位置；δ1和δ2分别为不同位置的滚子与滚道之间的接触变形量；w1和w2分别为不同接触位置处滚子与滚道之间的接触宽度。本文假设滚道表面的局部剥落故障采用矩形轮廓进行表征[4]。滚子进入局部剥落故障区间时，滚子与故障边缘位置发生接触。由于故障边缘的曲率半径不同于正常滚道，故滚子与故障滚道的接触变形和滚子与正常滚道的接触变形量存在差异，滚子与故障滚道的接触宽度和滚子与正常滚道的接触宽度也存在差异。为了准确地描述滚子通过局部剥落故障过程中滚子与滚道的接触状态，忽略滚子在运动方向的速度冲击对接触的影响，建立了圆柱滚子轴承滚子与滚道接触的等效模型，如图2所示。

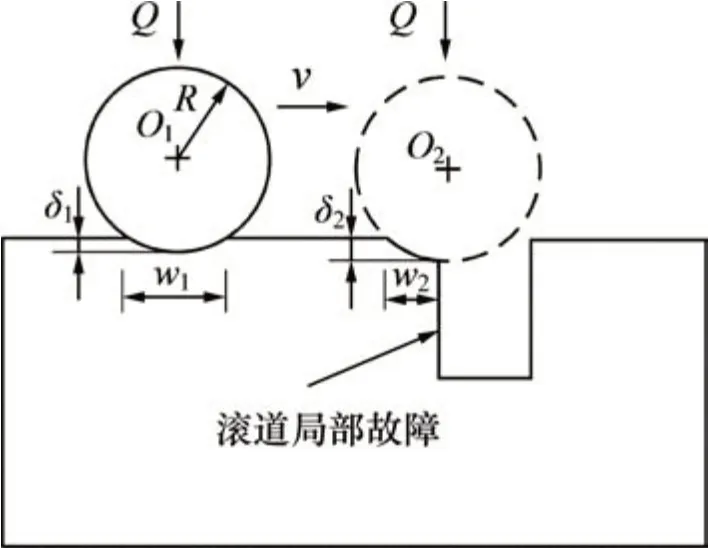
图1 圆柱滚子与滚道之间的位置关系Fig.1 Geometric relationship between roller and defect

图2 圆柱滚子轴承局部剥落故障等效模型Fig.2 Equivalent model of cylindrical roller bearing with localized spalling defect

圆柱滚子轴承滚子与滚道接触的等效模型[14]，如图2所示。从图2可知：滚道表面分为局部剥落故障区、过渡区与无故障区，矩形缺陷表示轴承局部剥落故障，XP为等效模型中轴承滚子与滚道接触的中心位置与轴承局部剥落故障中心位置的距离；Pmax为等效滚子中心位置的最大赫兹接触应力。等效模型的长度为10b，宽度为7b，其中，b为用赫兹接触模型计算得到的轴承接触半宽。接触半宽b表示为[15]

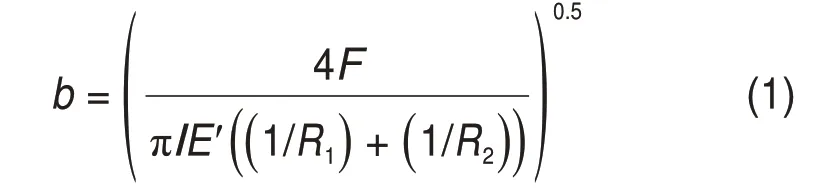
式中：F为作用在轴承上的径向载荷；R1为滚子半径；R2为内圈滚道半径；l为滚子等效接触长度；E′为等效弹性模量。E′的表达式为

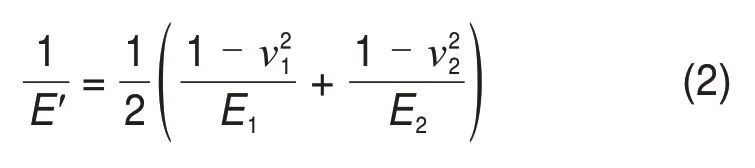
式中：E1和E2分别为滚子与滚道的弹性模量；ν1和ν2分别为滚子与滚道的泊松比。与滚道对应的滚子等效半径用R表示，其值取为

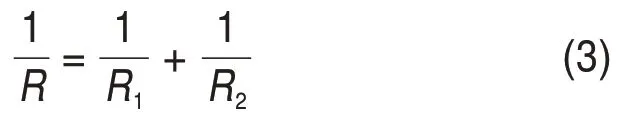
1.2 建立有限元模型

根据圆柱滚子轴承滚子与滚道接触等效模型(见图3)，以圆柱滚子轴承N306为例，建立含局部剥落故障的滚子与滚道接触有限元二维模型。该模型的宽度和高度与图2所示等效模型一致。其中，滚子半径为R1，局部剥落故障的深度为d，在接触位置对网格进行加密处理，单元网格边长应不大于接触椭圆的半轴长度[16]，单元长度取为1.5 μm，远离接触位置的单元长度逐渐增大。约束模型底部边缘，将载荷竖直施加在滚子中心，滚子与滚道之间接触的目标单元与接触单元分别为TARGE169和CONTA172[17]。

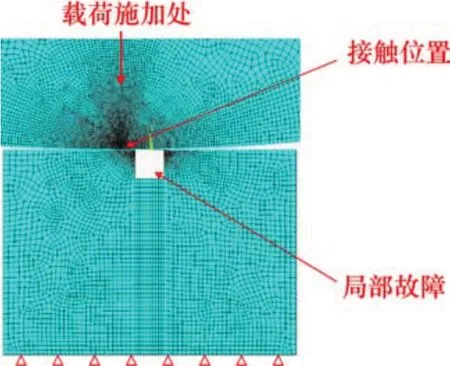
图3 滚子与滚道接触有限元模型Fig.3 Finite element model for contact between roller and raceway of cylindrical roller bearing

1.3 有限元计算理论

滚子与滚道接触有限元模型的求解过程中，有限元模型的刚度矩阵、位移矩阵和载荷矩阵的方程表达式为[18]

式中：K，u和F分别为滚子与滚道之间的接触刚度、位移和载荷矩阵。在获取有限元模型的节点位移之后，根据几何方程和材料的应力-应变关系，可计算获得有限元模型各结点的应变和应力。

为了准确求解滚子与滚道接触有限元模型中的接触变形，必须选择合适的接触算法求解。有限元方法常用的接触算法包括：罚函数法、拉格朗日乘子法以及增强拉格朗日算法[19]。罚函数法是将接触非线性问题转化为材料非线性问题，在接触面之间利用接触弹簧单元建立连接关系，该弹簧刚度被定义为接触刚度。接触体的接触压力与接触变形尺寸之间的关系可表示为[17]

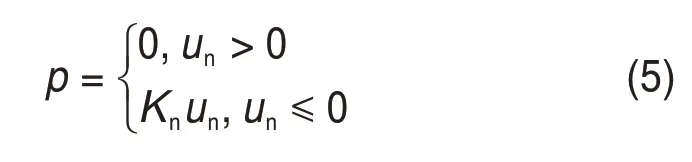
式中：p为接触压力；Kn为接触刚度；un为接触变形尺寸。为了找到精确的拉格朗日乘子，增强拉格朗日算法对罚函数进行的一系列修正迭代，其接触体的接触压力与接触变形尺寸之间的关系可表示为[17]

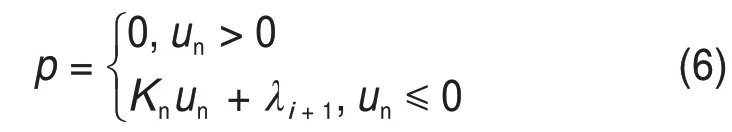
式中：

式中：ɛ为输入容差；λi为第i次迭代的拉格朗日乘子分量。然而，拉格朗日乘子法则不需要定义接触刚度，仅需定义颤振控制参数。理论上，拉格朗日乘子法在接触闭合时强制零穿透，在发生黏着接触时强制定义为“零滑移”。但是，拉格朗日乘子法增加了模型的附加自由度，需要额外的迭代来稳定接触条件，会增加计算成本。

1.4 等效模型验证

滚子与滚道之间的接触算法采用增强的拉格朗日接触算法，将有限元等效模型与数值计算方法进行对比验证。对于正常钢制圆柱滚子轴承，常用计算滚子与滚道之间的接触变形的方法为Palmgren经验公式[20]，即：

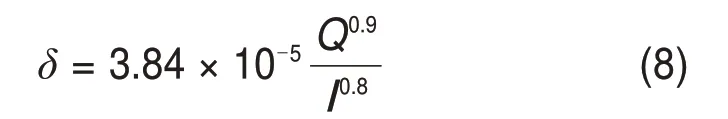
式中：δ为滚子与滚道之间的接触变形。利用式(8)计算正常滚子与滚道之间的接触变形，将计算得到的结果与有限元方法计算得到的结果进行对比，结果如表1所示。

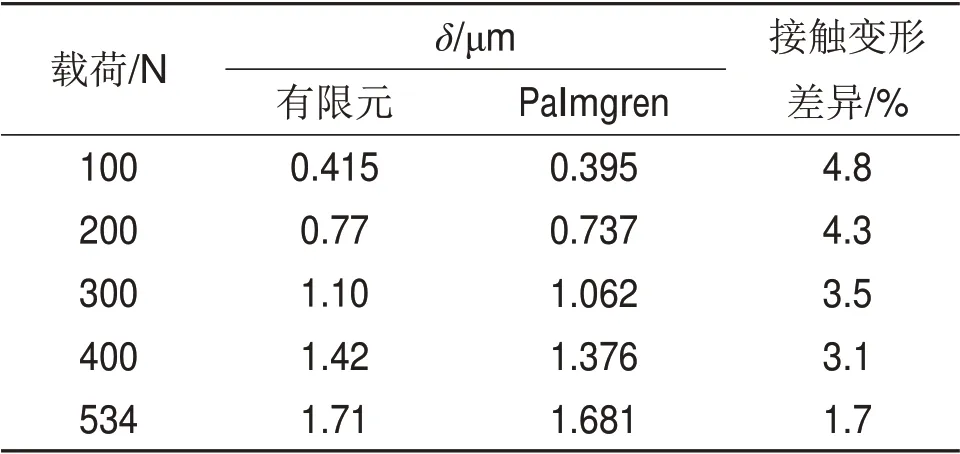
表1 有限元模型和Palmgren法计算得到的接触变形对比Table 1 Comparison of deformations between roller and raceway obtained from FEM and Palmgren’s method

从表1可知：当轴承径向载荷分布范围为100～534 N时，有限元计算得到的接触变形与Palmgren经验公式计算得到的接触变形之间的差异小于5%，故该有限元等效模型适用于研究圆柱滚子轴承滚子与滚道之间的接触特性。

2 局部剥落故障对轴承接触特性的影响

文献[15]的研究表明：对于圆柱滚子轴承，滚子与滚道之间接触宽度、接触变形和接触应力取决于滚子的径向载荷；接触宽度、接触变形和接触应力还与滚子半径、滚道半径和等效接触长度相关。然而，滚道表面出现局部剥落故障时，滚子与滚道之间的等效接触长度将出现变化，从而影响滚子与滚道之间接触宽度、接触变形和接触应力。

以圆柱滚子N306 研究对象，其几何参数如表2所示。该轴承的滚子直径为11 mm，内圈滚道半径为20.25 mm，滚子等效接触长度为11.4 mm，XP取为-1.5b～1.5b。本次计算选取25个等效接触位置进行研究。

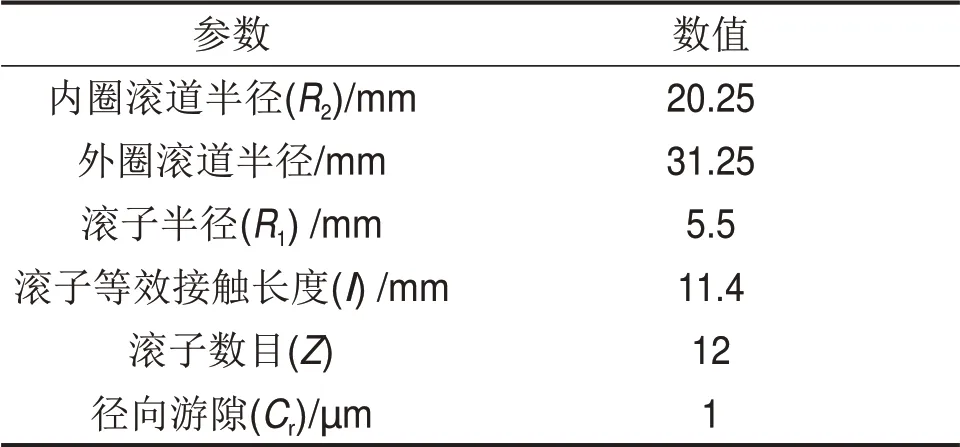
表2 圆柱滚子轴承N306的几何尺寸参数Table 2 Geometric parameters of a CRB N306

2.1 局部剥落故障对接触应力和接触变形的影响

利用图3所示的有限元模型求解滚子与局部剥落故障周围区域之间的接触变形、接触宽度和接触应力的分布状态。选取滚子的外载荷为19.5 N，方向定义为竖直向下。选取－1.5b≤Xp≤1.5b，b为式(1)中F取19.5 N 时对应的接触宽度，滚子的外载荷保持不变。图4所示为局部剥落故障宽度分别为0.5b，0.75b和b时滚子通过局部剥落故障区域滚道的过程中滚子与滚道之间接触变形量、接触应力和接触宽度。从图4(a)可知：当局部剥落故障宽度为b时，随着滚子与局部剥落故障边缘之间距离的减小，滚子与滚道之间的接触变形从0.563 μm 增大为0.812 μm，后又减小到0.682 μm，呈先增大后减小的趋势。从图4(b)可知：当局部剥落故障宽度为b时，随着滚子与局部剥落故障边缘之间距离的减小，滚子与滚道之间的接触应力从386 MPa 增大到1 644 MPa，呈增大的趋势。从图4(c)可知：当局部剥落故障宽度为b时，随着滚子与局部剥落故障边缘之间距离的减小，滚子与滚道之间的接触宽度从73 μm 减小为37 μm，呈减小趋势。仿真结果显示，随着局部剥落故障宽度的增加，滚子与滚道之间的接触变形量与接触应力也随之增加，而滚子与滚道之间的接触宽度则随之减小。

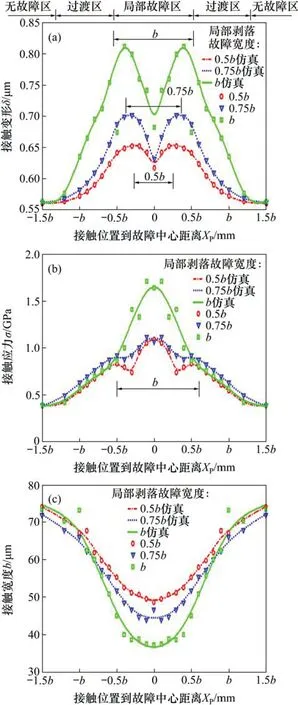
图4 滚道接触位置的变形、应力和接触宽度Fig.4 Deformation,stress and contact width of contact

图5所示为滚子通过局部剥落故障的过程中滚子与滚道上应力分布云图。从图5可知：滚子与滚道之间的最大接触应力所在的位置发生了变化，当接触点距离局部剥落故障边缘的距离较大时，最大接触应力位置位于接触点附近，在滚子趋近局部剥落故障边缘的过程中，最大接触应力位置逐渐移动到局部剥落故障边缘根部A，当滚子进入局部剥落故障区间时，最大接触应力位置到达局部剥落故障边缘顶部B。

2.2 局部剥落故障对接触刚度的影响

径向载荷与滚子-滚道之间接触变形的关系表达式为[21]

式中：n为载荷-变形系数。为了简化拟合过程，对式(9)两边分别取对数，可将指数型公式转化为线性拟合问题，从而获得不同接触位置时滚子与滚道之间的接触刚度，其表达式为

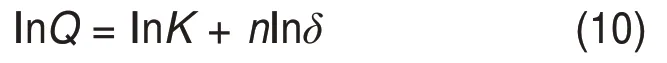
取XP=-1.5b到XP=1.5b过程中，不同载荷作用下滚子与滚道的接触变形，利用数值拟合的方式计算滚子与滚道之间的接触刚度。当滚子径向载荷从10 N 增大到25 N 时，XP从-1.5b增大到1.5b过程中不同局部剥落故障宽度下对应的滚子与内圈滚道之间的接触刚度，如图6所示。从图6可知：当局部剥落故障宽度为b时，滚子与滚道之间的最小接触刚度为1.18×108N/m1/0.7231，最大接触刚度为4.98×108N/m1/0.8957。随着滚子与局部剥落故障中心位置距离的减小，滚子与滚道之间的接触刚度先减小后增大，且滚子位于局部剥落故障区间时，滚子与滚道之间的接触刚度小于滚子与正常滚道之间的接触刚度。

3 局部剥落故障过渡区对轴承振动特性的影响

3.1 圆柱滚子轴承的动力学方程

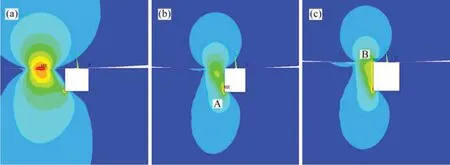
图5 滚子与滚道接触处应力分布Fig.5 Stress distribution between roller and raceway

图6 接触刚度变化规律Fig.6 Contact stiffness between roller and raceway

为研究局部剥落故障对轴承振动特性的影响，将轴承滚子考虑为非线性接触弹簧，引入文献[22]中的简化圆柱滚子轴承2 自由度系统的动力学方程，其表达式为

式中：min为内圈与转轴总质量；c为系统阻尼；K(θ)为滚子与内外圈滚道的综合接触刚度，其数值与图6中的一致；Fx和Fy分别为沿x和y方向的径向载荷分量；δi为第i个滚子与内外圈的接触变形。

任意角度θi下的滚子与内外圈滚道的综合接触变形为

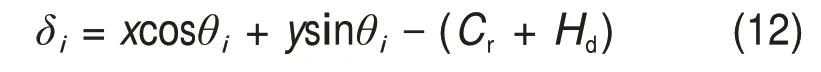
式中：Hd为滚子通过轴承滚道局部剥落故障位置的时变位移激励。时变位移激励Hd通常用半正弦函数表示[22]，考虑到轴承局部剥落故障过渡区对时变位移激励的影响，将其表示为

式中：Δθ=wt/rd；wt为过渡区的宽度；rd为局部剥落故障所在的套圈的滚道半径。

3.2 局部剥落故障对轴承振动响应的影响

运用定步长的四阶龙格库塔方法对方程(11)进行求解。时间步长Δt=5 μs，方程中轴承内圈与转轴的总质量min=1.2 kg，系统阻尼系数设定为350 N∙s/m[22-23]，转轴速度为4 000 r/min，施加在转轴上的载荷分别为Fx=400 N 和Fy=0 N。系统初始位移为x=1 μm 和y=1 μm。系统初始速度为0 m/s。圆柱滚子轴承N306的参数如表2所示。

取外圈滚道上局部剥落故障的宽度为0.5b和b，分别计算圆柱滚子轴承的振动响应。其中，局部剥落故障的深度都为b，过渡区宽度取局部剥落故障宽度的1/2，缺陷相对于X轴正方向的初始角位置θd0=0°，计算结果如图7所示。从图7可知：局部剥落故障的宽度为0.5b时，包含局部故障过渡区的轴承X向最大加速度为35.5 m/s2，而不含局部故障过渡区的轴承X向最大加速度为20.64 m/s2；局部剥落故障的宽度为b时，包含局部故障过渡区的轴承X向最大加速度为78.43 m/s2，而不含局部故障过渡区的轴承X向最大加速度为36.35 m/s2。对比结果显示，考虑轴承局部剥落故障过渡区时轴承振动加速度大于不考虑轴承局部剥落故障过渡区的轴承振动加速度。

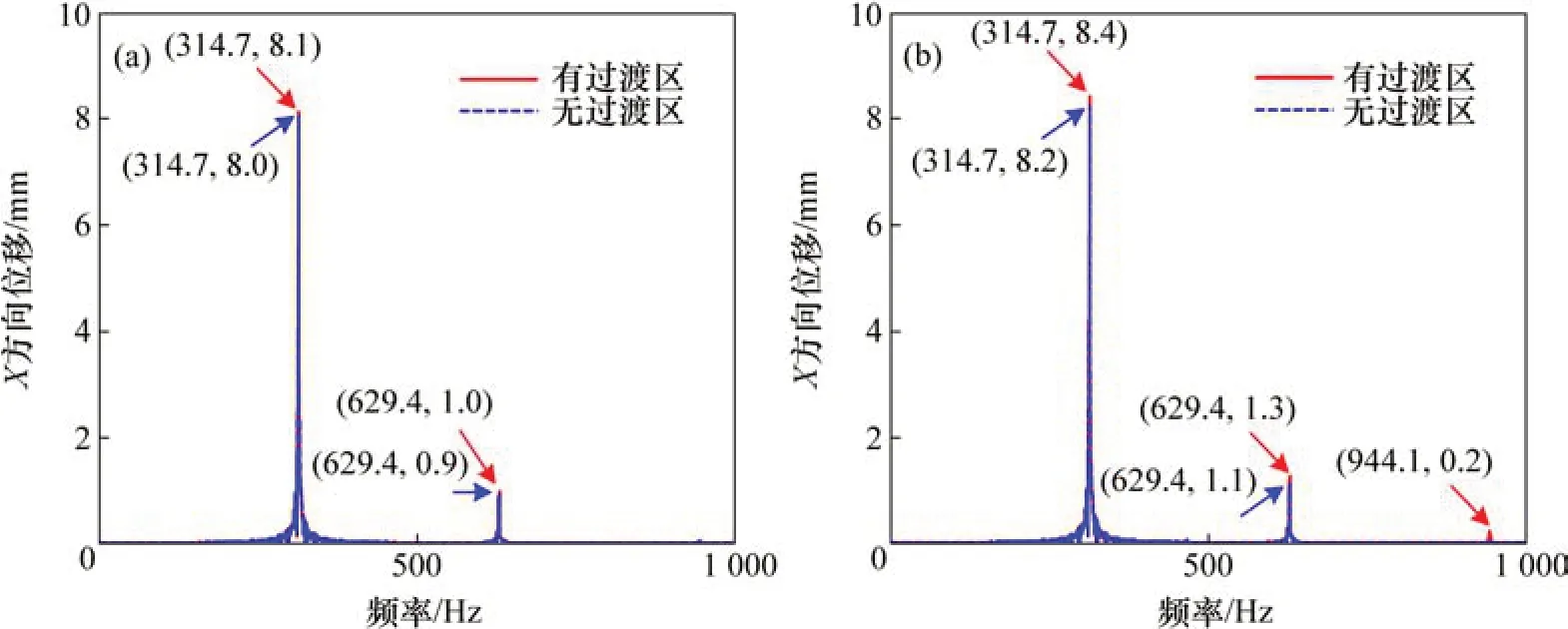
图8 不同剥落故障宽度对应的轴承X方向位移的FFT变换对比Fig.8 Comparisons of FFT inX direction of bearing with different spalling fault widths

外圈滚道上局部剥落故障的宽度为0.5b和b时，轴承X方向位移的频谱图如图8所示。从图8可知：2种故障宽度下都能获得相同的外圈通过频率及其倍频成分。2种故障宽度下获得的外圈通过频率均为314.7 Hz，与采用文献[15]的理论计算方法获得的结果一致，验证了仿真结果的正确性。

4 结论

1)当滚道存在局部剥落故障时，随着滚子与局部剥落故障中心位置距离的减小，滚子与滚道之间的接触应力增大，接触宽度减小，接触变形先增大后减小。

2)在滚子与局部剥落故障中心位置距离的减小过程中，滚子与滚道之间的最大接触应力位置由故障边缘根部移动到故障边缘顶部。

3)随着局部剥落故障宽度的增加，滚子与滚道之间的接触宽度减小，接触应力与接触变形量增大。

4) 滚子在通过局部剥落故障位置的过程中，滚子与局部剥落故障区域的接触刚度小于正常接触刚度。

5)在圆柱滚子轴承的动力学系统中，考虑轴承局部剥落故障过渡区时对应的轴承振动加速度大于不考虑局部故障过渡区的轴承振动加速度。