生长数学课堂下的复习课教学研究

山西省右玉县教育局 李光耀

广东省深圳市观澜第二中学 王振鑫

一、初中数学复习课存在的问题

笔者作为督导室主任，先后到所在区和全国各地的学校听课指导，发现复习课存在着很多棘手的问题，复习无目的性地开展、复习课以一张试卷从头讲到尾、学生没有任何思考、教师以罗列题目为主地复习等.这些低效的复习方式，都会使得学生的思维没有生长，甚至有的学生会对数学复习课失去兴趣，这也会极大地影响教育教学质量的提升.当前初中数学复习课都存在着哪些问题？这需要我们提高认识，改变教学方式，进而为教学增效.

1.本末倒置，使得复习课失去本应有的价值

数学复习课的本质是帮助学生梳理知识、构建知识体系，并在此基础上有所提升.有些教师认为复习课不重要，甚至有的教师为了赶教学进度根本不进行复习课的讲授.复习课应该是教师精讲，学生多悟、多练的过程，过多的教师讲解会使得学生没有思考的时间，会变得“两败俱伤”.

2.以题目式的训练满堂灌

课堂上，有的教师以一张试卷边做边讲的形式，也有的教师根据自己对教材内容的理解将题目分类然后印给学生做，有的教师从头讲到尾，甚至有的教师把试卷当成复习的测试卷.教师将答案和思路一股脑地灌输给学生，学生没有独立思考的时间和空间，完全被动式地跟着教师走，这样教出来的学生思维固化，不会创新.当前许多教师对数学复习课更多的是追求课堂的容量和学生练习的题量，导致学生认为复习课就是“炒剩饭”，重温旧知识、做题再讲题，有些乏味，降低了对复习课的兴趣.

3.重技巧、轻本质、忽视学科素养培养

教师上课时常出现用偏的方法和技巧给学生讲解题目，而忽视了题目的本质通法，技巧毕竟是对于少数题目而言，当学生遇到问题时，若不掌握通法则很难想到技巧.在这个过程中，很多教师的教学方法是死记硬背，而不是培养学生的思维，让他们学会独立思考，从而导致整体的教学效果差.

4.学生访谈，了解复习课现状实情

笔者对学生进行了访谈，倾听学生的真实想法，对研究策略有很好的借鉴作用.学生访谈实录如下：

生1：我觉得复习课就是试卷讲评课，一点儿意思都没有，没有激情，觉得上课很无聊.如果用问题串的形式来贯彻习题课的话，我觉得会让我很喜欢.

生2：复习课和常规课没什么区别啊，就是简单的知识点串讲，再做几道题就可以了，没什么太大的作用.

生3：我觉得复习课还是挺有用的，它不像新授课那么简单，难度会大一些，我很喜欢做难题，做出来超有成就感.

生4：复习课给我和同学的感觉就是无趣，大家都习惯了，刷题、讲题，老师不停地讲，我们不停地做，都习惯了.

生5：我比较喜欢老师分板块复习，能够帮我梳理学习内容，复习课挺好的，能够把我刚开始还没怎么学明白的内容给弄清楚.

生6：我很喜欢我们老师将一道题变化成多道题带我们进行思维的训练和复习，由易到难，同学们也都很喜欢.大家都愿意上这样的具有挑战的复习课.

二、初中数学复习课教学策略

1.从知识的碎片化学习到面向学生认知的整体构建

学生在对数学知识初学的过程中，通常是按照教材顺序逐一学习，他们的学习内容是碎片化、单一的，有时还是无序的.而复习课的主要功能是将知识系统化、网络化.这对学生系统学好数学，发展思维能力，对教师弥补教学中的缺欠，提高教学质量，有着至关重要的作用.因此教师要重视复习课的教学.如何根据学生的已有知识将其整合成体系呢？这之间的联系本身就是知识生长的过程.课堂中教师可以引导学生通过一个简单的题目进行题目间的内在变式和知识的生长，引发学生的思考并有效整合学生的知识.在这个过程中，引导学生自主发现知识间的内在联系，调动学生的参与度，引导学生构建数学思维导图（见图1）是一个有效的方法.

图1

2.精心选编教学内容，激发知识生长力

复习课不是做题课，更不是考试课，教师要认真准备备课素材，使得复习高效.复习课的内容选择有很多种方法.（1）知识板块化复习.教师将单元或某部分内容进行分类和整合，根据考点或知识的关联性将知识模块化，这样的复习设计思路清晰.（2）题组变式思维训练.教师从一道题（母题）出发，通过添加条件，如平移、旋转、翻折、改变原有题目条件、改变问题等，问题间呈关联性，真正把知识掌握与培养数学思维统一起来，不断引导学生思维的递进，这个过程本身就是学生数学思维生长的过程.（3）讲练结合式复习.在这种复习方式下，教师要精选题目，要避免题海战术，课堂上教师要给予学生充分的思考时间，教师再讲解.复习题选择的难度和数量要适中，不能够教师从头讲到尾，这样的方式是低效的，也是学生不喜欢的.

3.重视学生个体差异性，促进学生全面发展

在日常教育教学中，很多教师忽视学生的差异性，大部分教师只关注优秀学生的学习情况和学习进度，对于成绩好的学生偏爱，而忽视了那些成绩相对不好的学生的学习情况，这样，久而久之就造成了两极分化的局面.教师过分追求成绩，不能够及时采取有效措施来培养学生良好的学习习惯.每个人的兴趣爱好、学习习惯、生活环境、价值观等都不同，也会导致学生在教学过程中的差异性，教师不针对不同学生的特点开展有针对性的教学设计，便会使得复习课变成少部分人的培优课或补差课.

三、生长数学下的复习课设计原则

1.具有针对性

教师要认真分析学情，针对课程的学习情况和不同学生的掌握情况制定科学、合理的教学计划.内容上既要有梳理又要有变式练习，方式上要充分调动学生的积极性，给予学生足够的时间进行思考和分析，在课堂组织上要以合作式增加思维的碰撞.题目不可过多，教师要精选、要有代表性，在题型选择上尽可能不重复，尽量针对每道题都可以进行不同题型的拓展.

2.问题设置的关联性和递进性

课例：一次函数的复习课.

师：同学们，如图2，现在如果给出点A（1，2）和B（4，4），你能够得到哪些结论？

生1：我可以求出一次函数AB的解析式.

生2：我可以求在x轴上找一点P，使得|PA+PB|最小.

生3：我可以求在x轴上找一点Q，使得|PA-PB|最大.

生5：如果连接OA、OB、AB，则可以求出△AOB的面积.

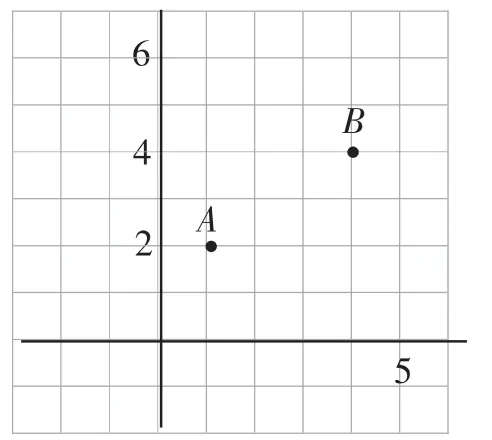
图2

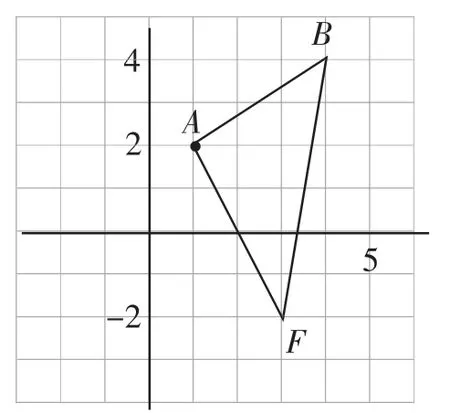
图3

师：如图3，如果再添加一点F，你们又有什么猜想呢？

生6：我可以求出△AOF的面积.

师：你们有哪些方法求△AOF的面积？（目的：引导学生复习在平面直角坐标系内求三角形面积的方法）

生7：如图4，用“矩形大法”，构建矩形，此时S△ABF=S矩形MNGB-S△ABM-S△ANF-S△BGF.

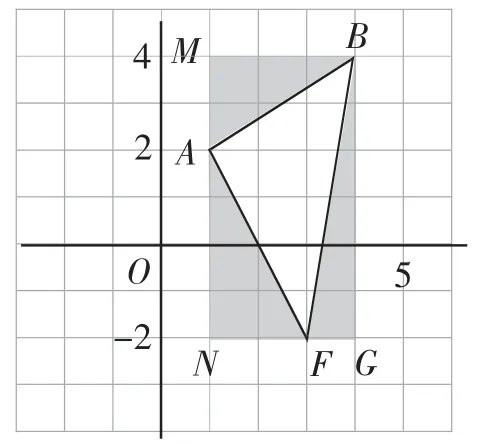
图4

图5

生8：如图5，我可以将刚才生7的方法进一步简化，不用构建矩形，构建直角梯形就可以了，S△ABF=S梯ANGB-S△ANFS△BFG.

生9：如图6，我想到了分隔三角形的方法，S△ABF=S△AMQ+S△MQB+S△BMN+S△MNF，我的想法是，分隔后的小三角形的边长尽可能位于平行于x轴或y轴的直线上，这样方便计算，而这个题目关键是求M、N和Q三点的坐标.

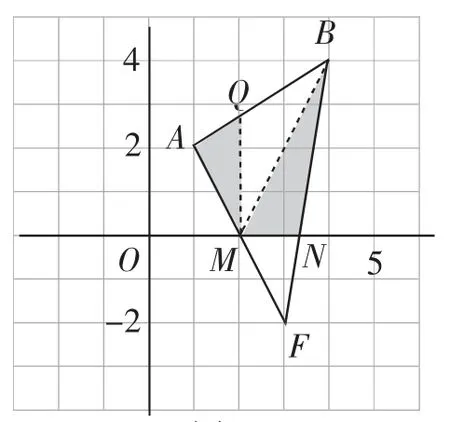
图6

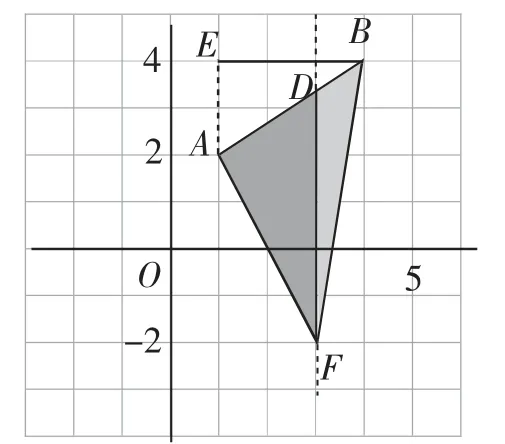
图7

生11：如图8，按上面这种思路，我还有其他的寻找铅垂高和水平宽的方法.

师：好的，既然说到了宽高公式，那我们就系统研究一下宽高公式吧.

师：如何证明图8-3呢？

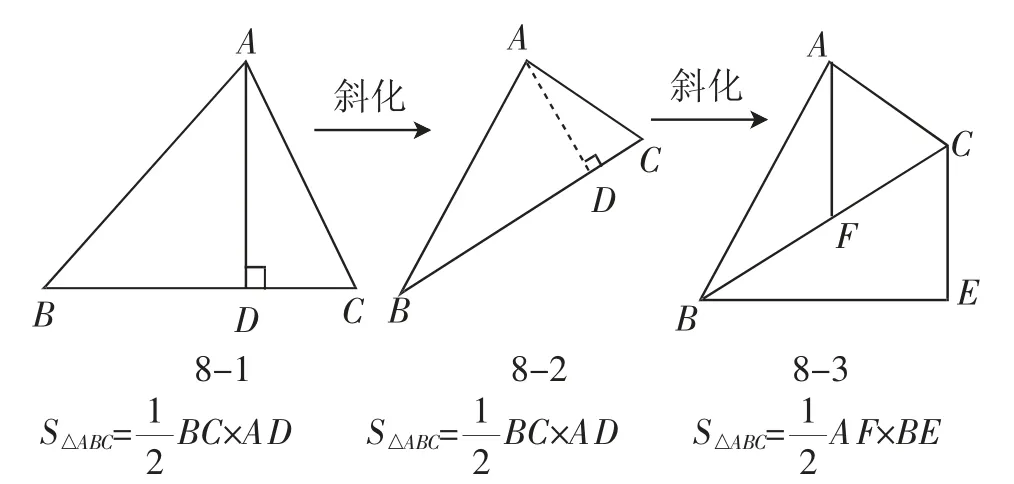
图8

生12：如图9，过点A作AG⊥BE于点G，交BG于点F.

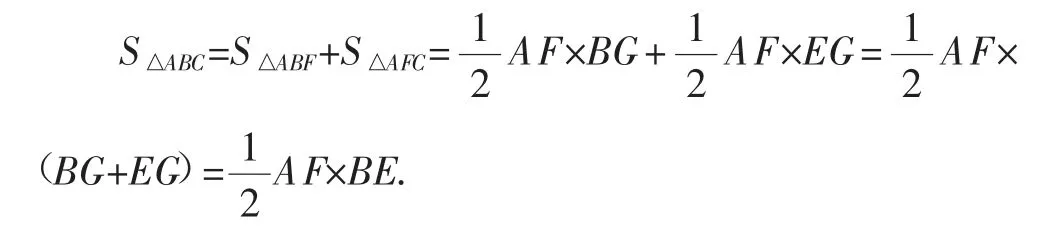
师：除了这种寻找铅垂高和水平宽的方法，你还可以怎样确定铅垂高和水平宽呢？

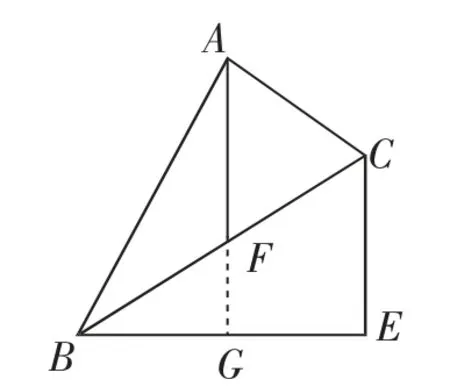
图9

图10

生13：如图10，过点A作AH∥BE，延长BC交AH于点N.

师：我们继续发散，现在还能研究些什么知识？

生14：可以研究在x轴上找一点T，使得S△ABT是直角三角形.如图11，以AB为直角边时，分别以A和B为直角顶点作线段AB的垂线，与x轴的交点就是所求.若以AB为斜边，则相当于以AB为直径构建一个圆，因为直径所对的圆周角是直角，此时这个圆与x轴无交点，因此这个题目中以AB为斜边的情况不存在.

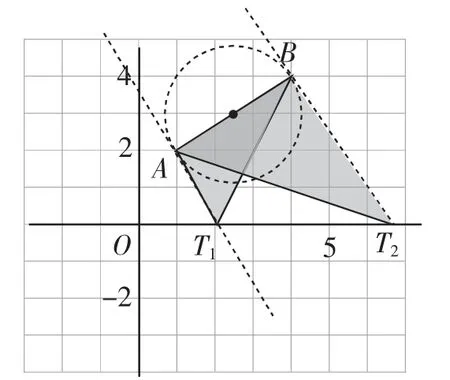
图11

师：按照这样的研究思路，除了能构建直角三角形，你们还有什么想法？

生15：还可以考虑构建等腰三角形.

师：请你在y=1这条直线上找一点I，使得以A、B、I为顶点的三角形是等腰三角形，请找到点I的坐标.

生16：如图12，如果以AB为腰，那就要分别以A和B为端点、AB为半径画圆，此时与直线y=1的交点就是所求（有四个）；如果以AB为底，那就要作AB的垂直平分线，此时交点为1个.所以本题共有5个交点.

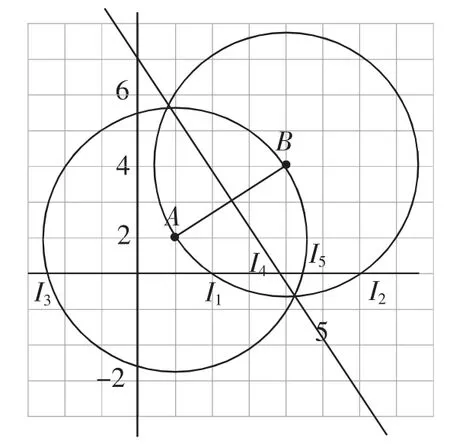
图12

思考：课堂上教师针对一个简单的题目，通过不断添加条件引发学生的思考，这不是单纯的添加条件，学生的思维从易到难，不断生长.这里既有知识的生长，也有学生思维的生长，潜移默化中提升了学生的数学学科核心素养.这样的课堂充满着挑战，充满着乐趣，更充满着学生的喜爱.