复习案习题的细节打磨：从封闭走向开放——从二次函数章末复习案打磨说起

江苏省海安市城南实验中学 谭志慧

最近一次备课组内集体备课中，研讨主题是二次函数章末复习案的打磨，笔者对其中一些打磨细节有了更深的认识，并引发后续思考，本文整理出来，与更多的同行分享、研讨.

一、二次函数章末复习案的打磨记录

案例1：在知识点简单梳理之后，继续复习二次函数的图像和性质，初稿安排了下面这道习题.

已知下列抛物线，填空：

y=x2+2x-3：开口向______，对称轴为______，顶点坐标为______，当x______时，y随x的增大而增大，函数有最______值；

y=1+6x-x2：开口向______，对称轴为______，顶点坐标为______，当x______时，y随x的增大而增大，函数有最______值；

打磨意见：这组习题的呈现方式是“密不透风”式的多空白填空，是封闭式问题呈现，可改为开放式问题，先给出4个二次函数的解析式，然后安排学生描述这些二次函数的图像和性质.其他学生在倾听后进行评价，教师适时追问：“你是从哪些角度进行描述的？”

打磨意图：先后给出4个不同的二次函数解析式之后，安排学生描述它们的图像和性质，有利于反馈学生对二次函数图像和性质的理解，并且能看出学生是如何研究图像和性质的，从哪些角度展开描述的，也就是函数研究的一般路径或“研究套路”.比如，对于函数图像，要关注它的形状、对称性、顶点坐标、图像在平面直角坐标系中的分布位置等；对于函数的性质，则可从函数的增减性、最大或最小值等角度进行分析.

案例2：为了训练学生数形结合地分析对二次函数一般式中系数符号的理解，安排下面这道习题.

二次函数y=ax2+bx+c的图像如图1所示，则a____0，b____0，c____0，2a+b____0，a+b+c____0，a-b+c____0.（填＞、＜或=）

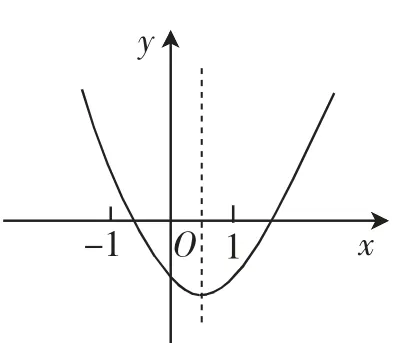
图1

打磨意见：这个题目是封闭式问题，可以修改如下.

问题1：你能说出系数a、b、c的符号吗？理由呢？

问题2：有同学指出代数式2a+b的值一定是正数，你觉得呢？

问题3：求证a+b+c＜0；

问题4：你们还能提出一个关于a、b、c的不等式吗？先在小组内交流，再在大组内展示.

打磨意图：初始问题是一道习题，但改编后以问题串形式呈现，使得问题成为问题串，有效驱动问题学程，让学生围绕图1进行了全面、深入的系数符号的分析，对一道习题达到了深刻理解的程度，并且从开始的封闭式设问走向了开放式设问.改编设问还体现了教师教学理念的转化，即从以教师为出发点的习题设计，眼中缺少对学生的思考，到改编成开放式的问题串，体现了教师眼中有学生，并且时时处处以学生为主体的价值观.

二、关于开放式教学的进一步思考

1.教师要转变教学价值观，重视学生主体地位的发挥

《义务教育数学课程标准（2011年版）》倡导教师要转化教学观念，确立以学生为主体的教学理念，体现了日常教学设计和课堂教学中，教师要时时处处心中有学生，而不只是停留在口号上.我们见到不少优秀的教学设计或课堂教学，明明一些教学环节是封闭式的，学生接受的是注入式教学，但教师在评课或所谓“赏析”时仍然大贴标签、大唱赞歌，认为这节课体现了以学生为主体之类的新课程理念.这些乱弹琴式的赞歌做法，说大话、说套话的教研风气需要批判，有追求的青年教师要主动防范这类不良导向.值得说明的是，重视学生主体地位的发挥，关键是在一些教学细节上得到彰显，比如，对某一道习题的封闭式设问，优化为开放式问题，这就是学生主体地位的体现.

2.教师要基于学程整体观，重视问题驱动式教学研究

教学设计时，教师要重视整节课的学程设计，而不是拘于某个习题、某个环节的精心预设，可以构思学程前后，加强不同环节之间的互动呼应，这样就可走向问题驱动式的教学研究.具体来说，上面案例1中，我们对原本“密不透风”式填空题进行改编设问，改成开放式问题，让学生结合函数学习与研究经验，自主归纳交流对这几个二次函数的理解，在整个教学进程中，这个环节不只是训练了这几个习题，而是通过这些习题的训练，引导学生全面梳理了二次函数的图像和性质的知识点，并能在具体问题情境中进行熟练运用.在案例2中，通过系列问题串引导学生分析出各项系数的符号特点，可以促进学生数形结合分析问题的能力，也能对二次函数的图像和性质达到较为深刻的理解.

3.教师要修炼专业基本功，重视命题改编能力的提升

郑毓信教授提出的数学教师的三项基本功（善于提问、善于举例、善于优化）得到不少一线教师的共鸣，在近年来《中学数学》（下）就刊发了很多关于善于提问、善于举例和善于优化的案例文章，这些文章读来非常接地气，常常能给我们以教学启发.就本文提到的案例来看，关键也是要修炼命题的专业基本功，而命题能力的背后就是教师善于提问的专业能力.问题呈现是否恰当，还可以怎样改进设问方式，都需要建立在教师深刻理解数学、理解教学、理解学生的基础上.需要防止一种认识偏差，这就是有些教师认为试题命制是一项专业要求很高的能力要求，自己没有机会参加一些地区或学校命题活动，也没有机会训练命题能力.事实上，就命题改编能力提升来说，教师在日常教学工作中要当成一种自觉追求，比如，针对一些例、习题的改编运用，就是重要的训练自身命题改编能力的机会.

4.教师要用好开放式问题，重视开放教学的课堂驾驭

数学考试时使用开放题可以让考生有多样化的表达，对开放题的研究也一度成为不少期刊上的一个热点话题，然而随着这类开放题的“阅卷成本”偏高或者存在很多主观成分，可能会影响开放题在评价中的信度，所以在很多较为重要的考试中开放题的身影越来越少，这是一种命题遗憾.但是在很多教学过程中使用开放题却成为越来越多教师的自觉追求，因为利用开放题可以促进开放式教学，让学生的学习兴趣得到充分调动.当然从开放题到开放的数学教学，对教师的课堂驾驭能力提出了较高的要求，这也是有些教师说课堂生成“易捕捉、难点评”的原因.特别是，面对学生的课堂生成，教师还要充分发挥教师的主导作用，对那些偏离教学主线、偏离课堂教学目标的学生发言要及时进行必要的干预或淡化处理，以便让学生的研究围绕教学主线，聚焦教学目标展示讨论和对话.

三、写在后面

教学即研究.我们从日常集体备课中的一些细节打磨和改进意图出发，思考了开放题与开放教学的做法，既有组内同行的共同意见，也有笔者个人的一些观点表达，既不一定准确，更不一定正确.期待更多同行围绕开放题和开放式教学深入讨论，丰富案例并优化开放教学的操作要义.