二阶线性齐次偏微分方程的几种解法及比较
2019-11-13 05:46:58孟晓仁
福建茶叶 2019年8期
孟晓仁
(中北大学信息商务学院,山西 晋中)
本文介绍3uxx+10uxy+3uyy-3ux-uy=0的三种解法以及这三种方法的比较。
1 三种解法
1.1 行波解法:

1.2 特征线法:


1 .3 微分算子法:
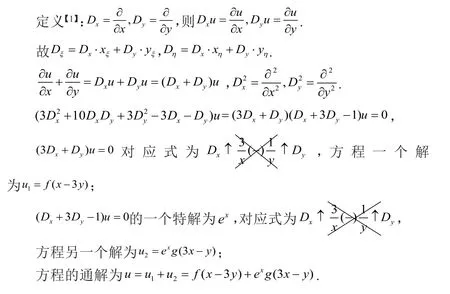
2 三种方法的比较
通过二阶线性齐次偏微分方程的三种解法的介绍发现,只要知道方程解的结构,设出解的形式,代入方程,会求导,会解一元二次方程,总可以求出方程的解,不需要积分的知识,这种方法大部分学生都能理解掌握,特征线法不仅需要高等数学中的积分知识,还要会求常微分方程,掌握求解常微分方程各种方法,难度较大,微分算子法比较简单,但是对于有些比较复杂的二阶线性齐次偏微分方程,微分算子法就非常难了,对于各项阶数相同的二阶线性齐次偏微分方程,微分算子法非常简单。三种方法各有优势。
猜你喜欢
中北大学学报(社会科学版)(2024年2期)2024-04-10 08:50:02
中学生数理化·中考版(2022年9期)2022-10-25 03:48:50
农业工程学报(2022年5期)2022-06-22 14:02:26
中学生数理化·中考版(2021年9期)2021-11-20 06:17:34
科学导报(2021年91期)2021-01-11 07:02:14
中北大学学报(自然科学版)(2019年6期)2019-11-22 07:39:14
无机化学学报(2019年5期)2019-05-07 07:28:12
中学生数理化·中考版(2017年3期)2017-11-09 02:07:37
初中生世界·九年级(2017年9期)2017-10-13 02:18:28
考试周刊(2016年90期)2016-12-01 20:14:25

