基于贝叶斯和F-measure感知机的分类器设计
马占杰,杨淑莹
(1.天津理工大学计算机科学与工程学院,天津 300384;2.计算机视觉与系统教育部重点实验室,天津 300384)
0 引 言
F-measure 又称为F-Score,是IR(信息检索)领域的一个评价标准,常用于评价分类模型的好坏,也是作为不同类型预测问题的性能指标,包括二分类、多标签分类(MLC)以及结构化输出预测的某些应用,如文本分块和命名实体识别等。与二分类中的错误率和多标签分类(MLC)中汉明损失等方法相比,F-measure 方法在少数类和多数类之间都表现出很好的平衡性,因此,在非平衡数据的情况下更适合。
传统的模式识别方法通常需要多个类别的样本,因此需要设计两个或多个类别的分类器。构建分类器方法有很多,如贝叶斯[1]、决策树、人工神经网络[2]、遗传算法、支持向量机(SVM)[3]遗传编程、粗糙集[4]、模糊判别等,在这些分类方法中,贝叶斯方法已经成为最引人注目的焦点之一,因为它的精度高[5],可以有效地处理不完整的数据。然而,当样本特征向量相互交织时,贝叶斯分类器容易出错。为了提高贝叶斯分类器的性能,提出一些方法和技术,例如,树扩张型贝叶斯(TANB)、Generalized Naive Bayes 分类器[6]。 TANB 算法通过查找属性之间的依赖关系来减轻朴素贝叶斯中任何属性之间的独立性假设。在学习参数方面,TANB 模型比朴素贝叶斯模型面临更多的困难,特别是在训练集数据较少时。GNB 认为整个数据集只有一个概率依赖关系,当整个数据集单一分布时,GNB 性能会更好,但是,当整个数据集不是单一分布时,GNB 性能较差,近年来,评估措施在分类器分析和设计中起着至关重要的作用。准确率、召回率、精度、F-measure、Kappa、ACU 等新的措施已经被提出[7]。F-measure 被认为是测试有效性的重要措施[8]。由于Bayes 和F-measure 的优势,本文结合了两者对不平衡数据进行分类。
当大多数类的输出数量远远超过其他几个类时,很难将错误的样本与这几个类别分开。近年来,研究人员在不平衡问题上做出了很大的努力,并得到了更好的解决方案[9],例如,改变类分布,结合决策成本,在学习过程中用性能测量来替代标准算法的准确性。大多数方法更适合于平衡域中的分类。
本文提出一种不同的方法来解决这个问题,给出一种基于贝叶斯和F-measure 的新的分类器算法。所提出的算法不会改变类的分布和任何决策成本。首先计算后验概率,当样本不在混合交叉域时,本文应用Beyes分类器进行分类。其次,当样本处于混合交叉域时,本文采用新的框架对易错分类区进行分类。
1 在条件分布密度的混合交叉域内的F-measure感知器
当样本在混合交叉域内时,贝叶斯分类器容易出错。感知器算法适用于小样本,它是收敛算法,具有计算简单、存储容量小和易于实现等优点。F-measure 在分类器分析和设计中起着至关重要的作用。F-measure被认为是测试有效性的有效措施。
1.1 F-measure 评估标准
当样本特征相互依存时,分类容易出错。为了解决这个问题,本文提出一种新的分类算法。
在本文中假设有两个类ω+,ω-,定义C={ω+,ω-}为可能类的集合,其中,ω+表示为正相关类,ω-表示为负相关类。TP(Ttrue Positive)表示类别为ω+的样本被系统正确判定为类别ω+的数量,FN(False Negative)表示类别为ω+的样本被系统误判定为类别ω-的数量,显然有P=TP+FN;FP(False Positive)表示类别为ω-的样本被系统误判定为类别ω+的数量,TN(True Negative)表示类别为ω-的样本被系统正确判定为类别ω-的数量,显然有N=FP+TN。
定义如下参数:
平均精度A(accuracy)反映了分类器系统对整个样本的判定能力:

召回率:
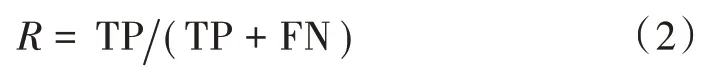
准确率:
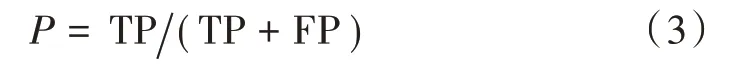
F-measure(F1score orFscore)是准确率(Precision)和召回率(Recall)的加权平均值:
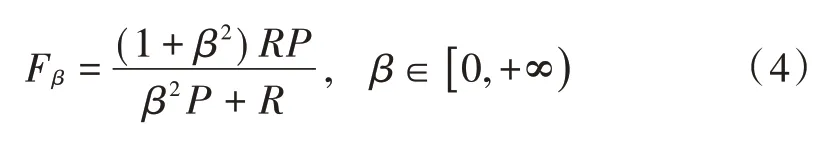
P和R指标往往出现矛盾的情况,为了综合考虑,本文利用F-measure 作为适当的评估标准。
为了最大化训练分类器的性能,必须找到适当的区域Ω+,Ω-。FN,FP,TP,TN 可以通过以下公式计算:
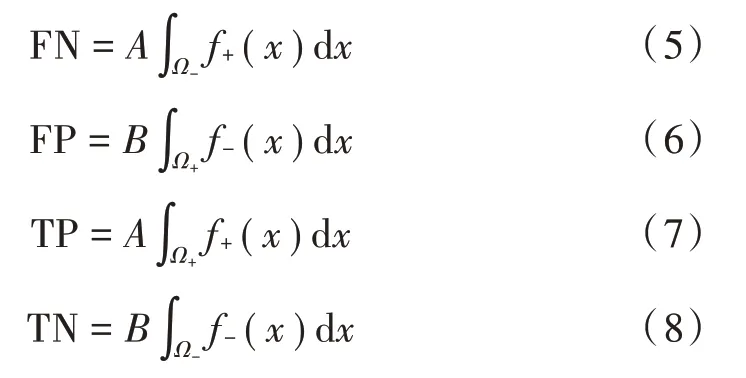
式中:A和B是训练数据ω+类和ω-类中的个体数,分布函数满足:

1.2 普通感知器
由于函数f(W)的数值解通常只是某种意义上的最优解。 定义准则函数,然后在最大或最小的条件下使此准则函数找到解f(W)。梯度下降法确定准则函数J(W),然后选择初始值W(1),迭代公式如下:
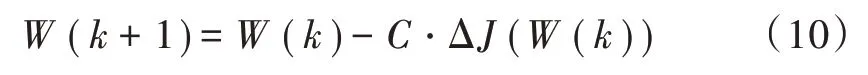
J(W)可以选择如下:
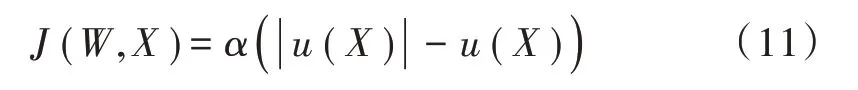
下一步是求解使J(W)达到最小解的W。W(k)定义为W的第k个迭代解,W(k+1)是k+1 次迭代解。
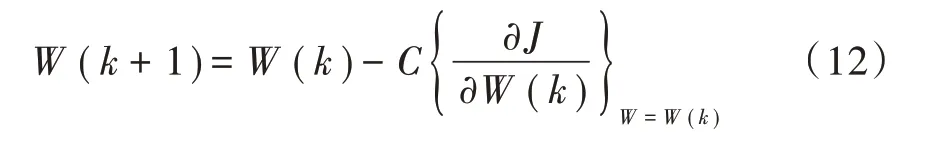
式中C是校正系数。
假设α=1/2,方程(11)可以重写如下:

式(12)可以表示如下:

当u(X)>0 时,表示样本正确分类,W(k+1)=W(k),无需修改权重;否则,当u(X)≤0 时,表示样本错误分类,W(k+1)=W(k)+CX(k),需要修改权重。普通感知器只考虑调整单个样本,而不考虑样本分布的调整。为了解决这个问题,本文提出F-measure感知器算法。
1.3 F-measure 的最优边界确定
传统的贝叶斯分类器是使后验概率最大化,改进的算法是使F-measure最大化。最大化F-measure等于最小化E:

根据式(12)~式(14),E表示为:
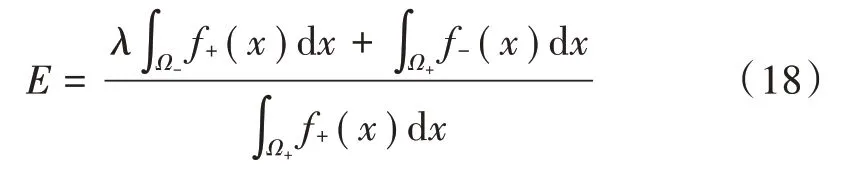
为了最小化E,可以使用辅助函数u(x)来表达问题。当x∈Ω+时,u(x)>0;x∈Ω-时,u(x)<0。
方程(18)可以表示如下:
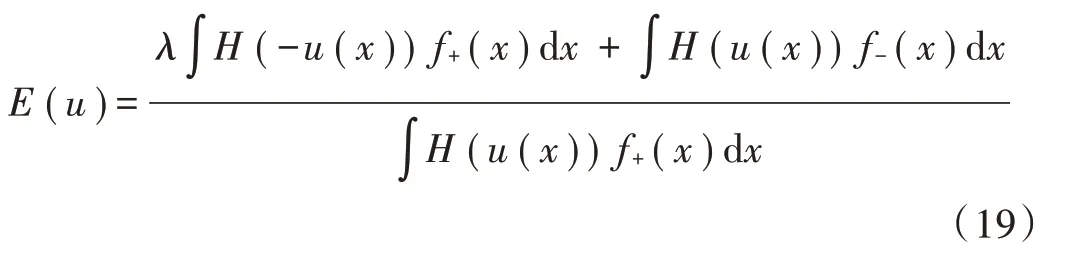
式中H(y)是平滑的单位阶跃函数。式(19)的一阶导数如下:
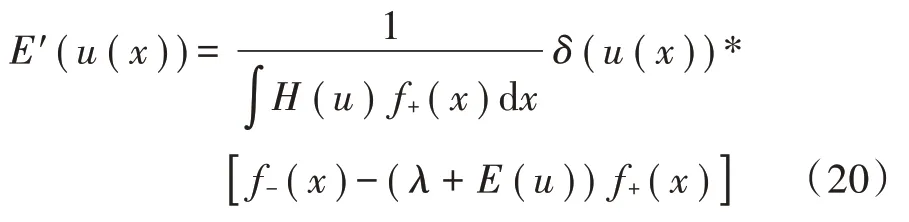
式中δ(y)是平滑的狄拉克函数。

u(x)通过式(21)获得。梯度下降法用于求解方程(21)。具体来说,使用初始化的u0来求解偏微分方程。
当偏微分方程达到稳态时,式(21)得到满足。
本文首先计算样本的后验概率。如果后验概率大于阈值,则样本不在容易出错的区域中。如果后验概率的最大值小于或等于阈值,则样本处于容易出错的区域,然后采用新方法进行分类。对于n维空间,样本由矢量X=(x1,x2,…,xn)T表示,识别函数如下:
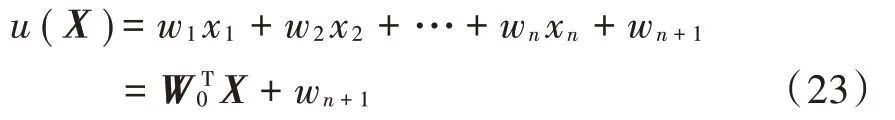
式中:W0=(w1,w2,…,wn)T是权重向量。在样本向量的末尾添加元素1。式(23)可以写为:

训练过程获得权重向量W,使用梯度下降法计算W。式(19)可以重写为:

式(20)可以重写为:

W通过迭代计算获得:

矢量的方向主要取决于最大分量的值。负梯度矢量表示最速下降的方向。当梯度矢量为零时,它可以达到函数的极值。如果可以达到极值,得到式(21)的最优解。W(k)被定义为W的第k个迭代解,W(k+1)是第k+1 次迭代解。

其中C是校正系数。
边界确定的具体步骤如下:
1)权重向量的初始值为0,W0=W1=W2=…=W9=0。
2) 计算第k次迭代的结果,ui[X(k)]=
3)如果δ(WTX)=0,则不需要修改权重;如果δ(WTX)=1,则需要修改权重。
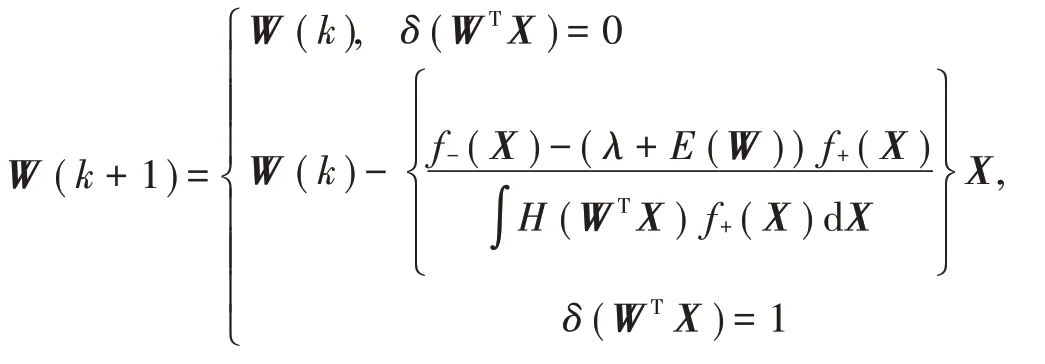
式中:
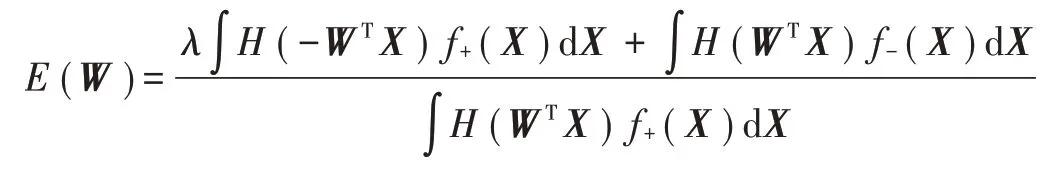
4)返回到步骤2)循环,直到权重不需要修改。
5)测试样品的特性用于计算式(24)。
6)根据u(X)的正或负判断类别:

2 实验结果
将本文提出的方法用于齿轮故障诊断,使用100 个正常齿轮样本和30 个异常齿轮样本的不平衡数据集。小波包和包络谱的能谱用于故障诊断。正常齿轮有100×9 个特征,异常齿轮有30×9 个特征。去噪后的齿轮故障信号波形如图1 所示。故障信号由3 层小波包分解,得到8 个频带能量,如图2 所示。小波包分解后的能量分布可以清楚地显示故障信息齿轮,证明故障诊断有用。异常齿轮的包络谱如图3 所示。
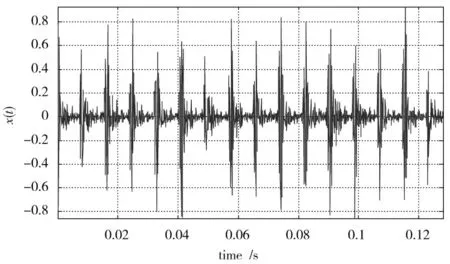
图1 去噪后故障齿轮的信号Fig.1 Signal of fault gear after denoising
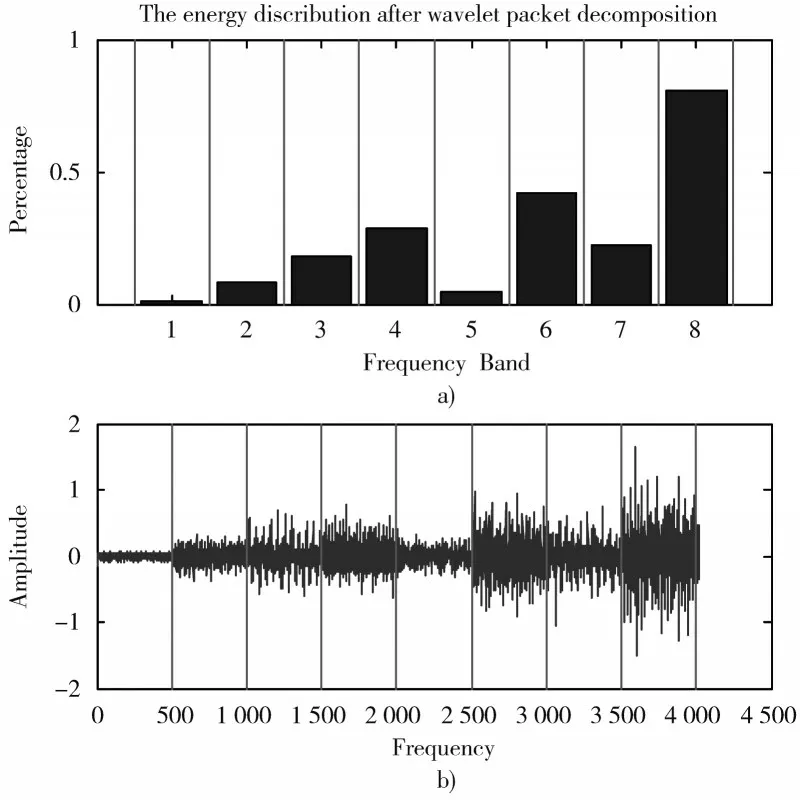
图2 3 层小波包分解后的能量分布Fig.2 Energy distribution after decomposition of 3-layer wavelet packet
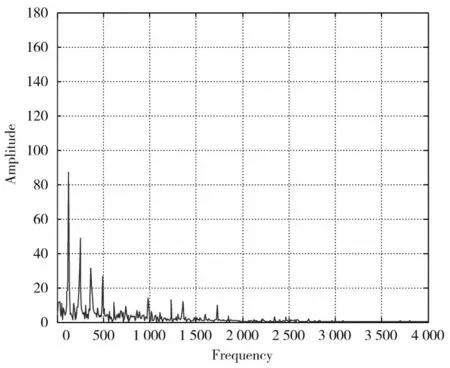
图3 故障齿轮的包络谱Fig.3 Spectrum envelope of fault gear
将本文提出的算法与传统的朴素贝叶斯分类器进行比较。图4 显示了所提出的算法和传统的朴素贝叶斯分类器在β变化时的鲁棒性。表1 给出了实验结果的详细情况,每个算法执行5 次。所提出算法的参数为β=1,C=1。实验的收敛速度取决于初始向量W(1)和C。从表1 可以看出,朴素贝叶斯分类器具有差的F-measure、召回率和准确率。本文所提出的算法得到了更好的F-measure,得到了更高的召回率和准确率。由于样本的特征向量不是完全独立的,所以本文提出的方法比传统的朴素贝叶斯分类器具有更高的识别率。
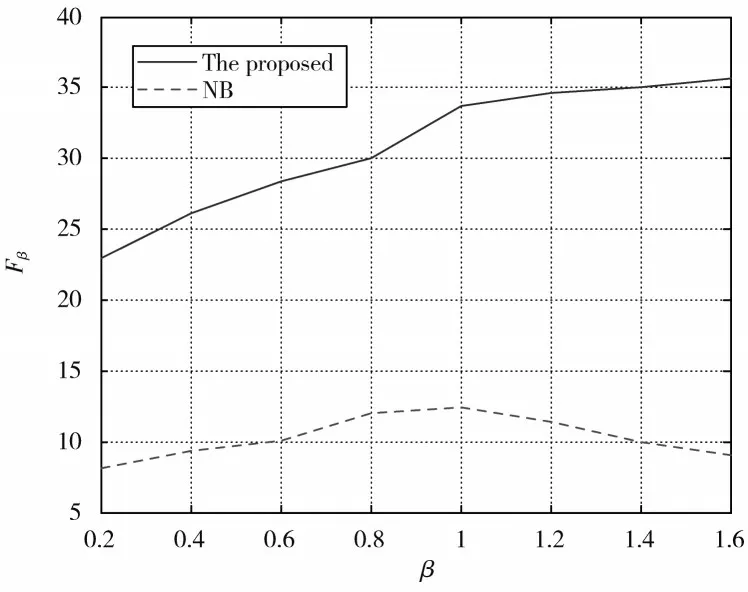
图4 算法鲁棒性对比Fig.4 Comparison of robustness of algorithm
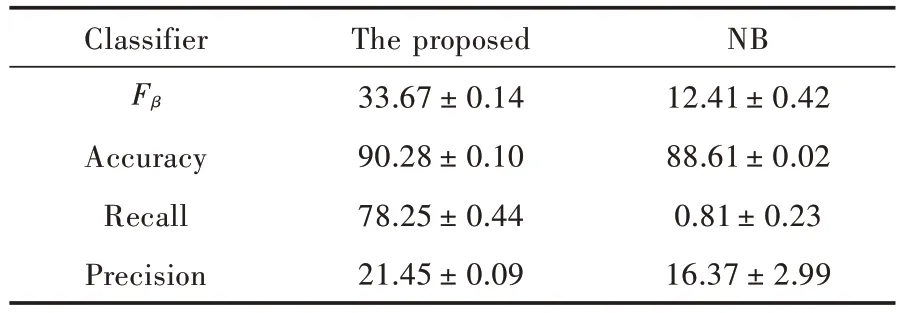
表1 每个算法超过5 次执行的性能值Table 1 Performance values for more than 5 times executed by each algorithm%
对于实验验证,用KEEL 数据集[10]中提供的公开实际数据进行了实验验证。对多类数据集进行修改以获得两类不平衡问题,以便一个或多个类的联合成为正类,其余类中的一个或多个类的联合被标记为负类。表2 给出了实验研究中使用的不平衡数据集的描述。表2 中显示的信息包括:数据集名称(数据集);属性数(Atts.);样本数(Ex.);少数群体和多数群体的百分比(%min;%max);不平衡比(IR)。
在研究中,将提出的算法与普通感知器、结合贝叶斯和梯度下降的感知器以及传统的朴素贝叶斯分类器进行比较。每个算法进行10 次交叉验证。应用95%置信水平的双尾t检验系统地比较NB 算法、普通感知器算法和结合贝叶斯和梯度下降的感知器算法的分类精度。在图5 中,通过使用5 个数据集获得Fβ值。所提出的算法具有最好的结果。表3 给出详细实验结果。实验结果表明,随着不平衡数据的增加,NB、普通感知器和结合贝叶斯和梯度下降的感知器算法的分类精度逐渐降低。与这三种方法相比,本文提出方法的分类精度最高。虽然提出方法的准确性随着失衡数据的增加而减小,但平均准确率为90.42%。
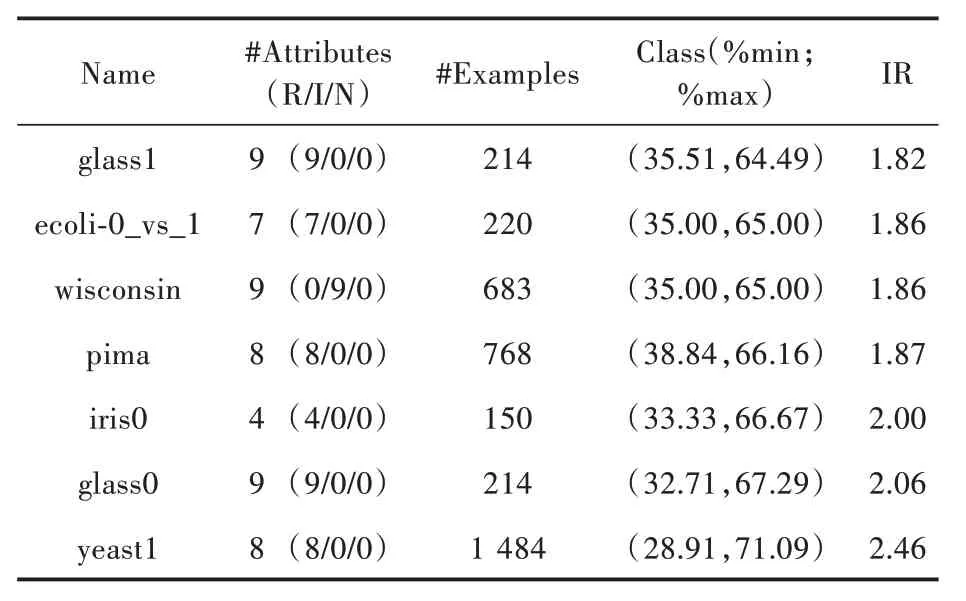
表2 不平衡数据集的描述Table 2 Description of unbalanced data set
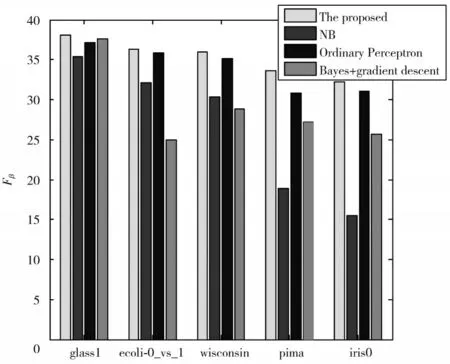
图5 不同算法的Fβ 值Fig.5 Fβ values of different algorithms
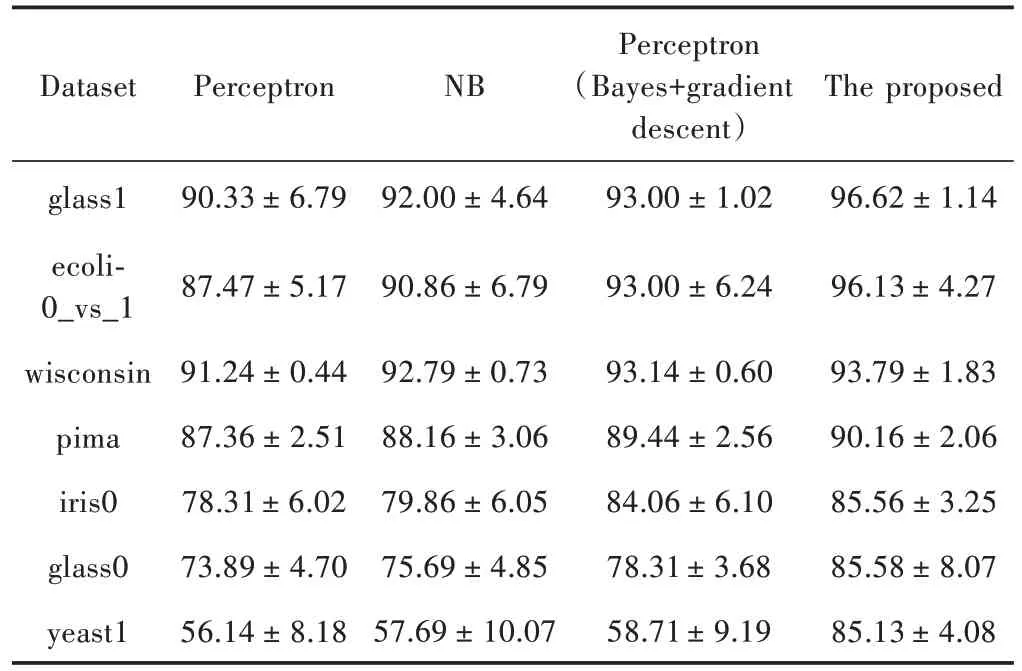
表3 分类精度比较Table 3 Comparison of classification accuracy %
3 结 论
本文提出一种新的分类算法处理不平衡问题,尤其在样本特征相互依赖时。首先计算后验概率以判断样本是否位于易错区域。采用该算法对易于误分类的样本进行分类,在研究中,将所提出的算法与传统的分类器方法进行了比较,实验结果证明了该方法的优越性。

