基于GA-ACO-BP的WSN数据融合算法实现

游志勇，苏彦莽，王羿帆，高小婷

（1.河北工业大学电子信息工程学院，天津 300401；2.河北工业大学天津市电子材料与器件重点实验室，天津 300401）

0 引 言

无线传感器网络（Wireless Sensor Network，WSN）是由长期部署在监测区域内的无线传感器节点互相通信形成的多跳自组织系统[1]。无线传感网络技术已广泛应用于工业控制、智能家居、军事安全、空间探测、精准农业、环境监测等诸多领域。由于传感器网络节点主要依靠电池供电，频繁更换电池势必造成人力、物力的大量消耗，所以必须要高效率地使用能源，延长传感器网络的工作周期。传统的数据监测系统在信息采集和处理方面存在着一些缺陷[2]。传感器节点的通信距离和处理能力有限，单节点只能提供部分信息，因而，传感器节点在监测范围采取互相交叉重叠的方式部署，以获得对象完整信息，但这会导致节点间数据冗余严重[3]。无线传感器网络数据融合技术能有效去除数据冗余性，减少通信开销从而降低能耗，延长网络寿命[4]。

为有效去除数据冗余性，信息采集能耗大，延长网络寿命等问题，专家学者提出大量的数据融合算法对数据进行网内处理，提高网络收集数据整体效率。文献[5]提出一种数据分批估计自适应加权融合算法，在一定程度上提高了数据的精确性，但并没有加快数据融合进程，网络寿命没有得到明显的改善。文献[6]提出在WSN中基于BP神经网络的数据融合方法，加快了BP神经网络的收敛速度，降低了数据冗余度，但网络结构选择不一，通常由经验选定。文献[7]提出基于蚁群算法的BP神经网络ACO-BP 方法，有效地降低了网络时延，无线信道频谱资源得到充分的利用，但ACO 存在初始信息素不足，寻优时间长，易陷入局部最优状态的缺点。本文基于前人提出的算法基础上，为解决WSN 中数据冗余度高，减轻网络的传输拥塞，降低数据传输延迟，提出一种智能化的数据融合算法——GA-ACO-BP（BP Neural Network Multisensor Data Fusion Algorithm Optimized by Genetic Algorithm and Ant Colony Optimization）。GA-ACO-BP算法利用遗传算法搜索最优解来初始化蚁群算法信息素分布，遗传算法随机生成的种群加快了蚁群算法收敛速度，避免陷入局部最优。优化后的蚁群算法更新BP神经网络模型的权值和阈值，优化目标函数收敛速度，提高数据精确度，采用GA-ACO-BP 算法对传感器采集的数据进行融合，可以减少网络的通信量，节省能耗。

1 网络模型

LEACH（Low Energy Adaptive Clustering Hierarchy）是MIT 的Heinzelman 等人为WSN 提出的一种低功耗自适应聚类路由协议。LEACH 协议的特点是分级和数据融合，节点自组织成簇，选出若干个簇头，簇内成员通过CSMA MAC 协议将采集的数据发送至簇头，由簇头将信息发送至Sink 节点，在下一次循环中重新选择簇首进行数据传输，本轮数据通信阶段选定的簇头不会在下轮簇头的选取中再次被选中，簇头主要完成簇内成员数据融合并与汇聚节点进行通信，因此，簇头的能量消耗非常大，为均衡地消耗网络节点能量，各节点等概率地选为簇头。采用LEACH 算法的WSN部分网络结构如图1所示。

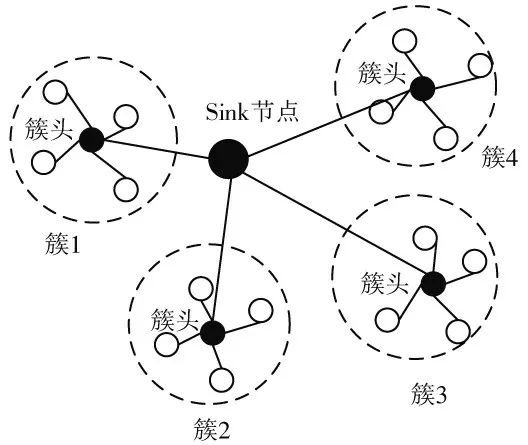
图1 部分网络结构Fig.1 Partial network structure

2 算法基础

2.1 遗传算法

遗传算法（Genetic Algorithms，GA）是受到进化理论启示所发展的可计算模型之一，是一种借鉴生物界的进化规律发展而来的“生存+检测”的迭代过程的全局搜索算法。其基本原理是把问题的解表示成染色体，通过选择、交叉、变异等操作产生下一代的染色体，并逐步淘汰适应度函数值低的染色体，增加适应度函数高的染色体，经过n次迭代后，最终生成适应度函数值很高的染色体。遗传算法的三个基本操作如下：

1）选择算子。选择的目的是把适应度高的个体，直接遗传或配对交叉使之有机会成为父代种群，使用选择算子对群体中的个体进行优劣淘汰操作。

2）交叉算子。交叉算子是遗传算法的关键步骤，将种群中各个个体随机配对，每一个体以交叉概率（Crossover Rate）来交换它们之间的部分染色体，体现了信息交换的思想。

3）变异算子。在群体中随机选择一个个体，以较小的概率对其基因座上的基因值进行改变，模拟生物进化的偶然事件。

2.2 蚁群优化算法

蚁群优化（Ant Colony Optimization，ACO）算法是通过模拟蚁群的协作觅食过程的计算算法，是一种基于种群寻优的启发式搜索算法[8]。其基本原理为：用蚂蚁觅食路径表征待优化问题的可行解，所有蚂蚁行走的路径构成优化问题的解空间，较短路径上蚂蚁释放的信息素量较多，蚂蚁优先选择信息素浓度大的路径作为最优路径，并释放信息素，最终选择这条路径的蚂蚁数量越来越多，在正反馈作用的机制下集中到最佳路径上，此时对应的便是待优化问题的最优解。设存在n座城市，m只蚂蚁，dij（i,j=1，2，…，n）为城市i，j的间距，τij(t)为t时刻在城市i，j路线上的信息素浓度，k为蚂蚁根据信息素浓度选择的路径，pk ij(t)表示t时刻蚂蚁k在i城市走向j城市的概率，公式如下：

蚁群算法搜索过程采用分布式计算方式，多个个体同时进行计算，加快了算法计算能力和效率，采用正反馈机制，搜索过程逐步收敛，最终逼近最优解。将遗传算法引入蚁群算法系统，每一代形成的解作为初始种群，反复迭代，得到p，α，β的最优组合，加快蚁群算法的收敛速度。

2.3 BP神经网络

BP神经网络（Back Propagation Neural Network）是一个基于数学统计学类型的学习方法（Learning Method）逼近目标函数，从多种角度对生物神经系统不同层次的抽象和模拟，包括工作信号正向传递子过程，误差信号反向传递子过程。无线传感网络存在大量的节点，每个节点相当于神经系统的神经元。通过对大量数据进行运算和处理，得到能够反映数据特征的结论性结果[9]。BP神经网络拓扑结构如图2 所示，分为三个层次，分别是输入层、隐含层、输出层。

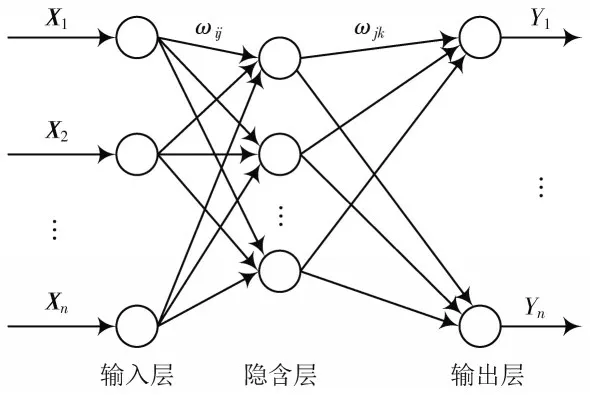
图2 BP神经网络拓扑结构Fig.2 Topological structure of BP neural network

图2 中，X1，X2，…，Xn是神经网络的输入向量，ωij是输入层到隐含层之间的权值，ωjk是隐含层到输出层之间的权值，Y1，Y2，…，Yn为网络实际输出值。

BP神经网络数学理论证明了它能实现任何复杂非线性映射功能，有很强的自学习、自适应能力。但它的权值通过局部改善逐步调整，存在局部极小化问题，且BP神经网络算法收敛速度慢，初始权值具有随机性，需要长时间的学习训练。

3 算法实现

本文基于LEACH 协议构建无线传感网络路由协议，根据BP神经网络模型，簇内形成的簇头为人工神经网络输出层，节点组成的簇为人工神经网络的输入层，隐含层节点的个数根据经验式（2）可得：

式中：h为隐含层节点个数；m为输入层节点个数；n为输出层节点个数；a为1～10 之间的调节常数。

GA-ACO-BP 算法实现流程图如图3 所示。确定BP神经网络的神经元个数、神经网络的连接权值、阈值，每只蚂蚁从隐含层节点构造解空间，如果蚂蚁选择了该节点，根据上一层的权值和阈值的集合中选取一个元素，否则，跳转至下一节点。同时，根据规则更新信息素。在蚁群算法中加入遗传算法的交叉算子和变异算子，对待交叉的个体适应度值进行重构，变异过程采用高斯方法的正态随机数替换基因序列，计算出适应度值，查看是否达到目标要求，若达到将最优解传输至BP神经网络训练，否则当前迭代次数加1，清空路径记录表，构造解空间，直至算法满足终止条件。BP神经网络对蚁群算法的寻优结果进一步训练，计算预测误差，更新权值、阈值。

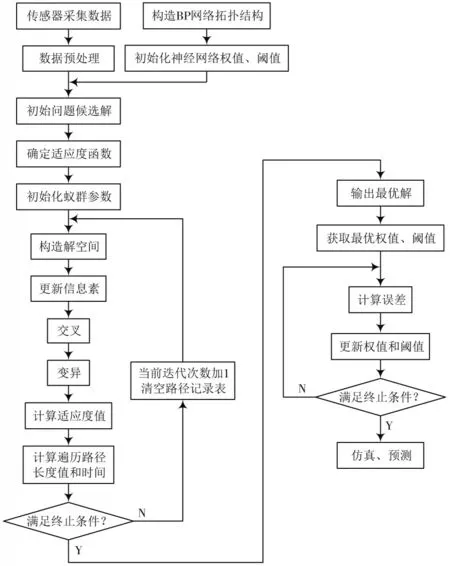
图3 GA-ACO-BP 算法流程图Fig.3 Flow chart of GA-ACO-BP algorithm

主要步骤为：

1）确定BP神经网络结构，初始化设置，包括输入层-隐含层的权值ωij，隐含层阈值αj，隐含层-输出层的权值ωjk，输出层阈值βq，记所有参数为q1,q2,…,qn，形成一个随机可取任一一个不为零的元素集合Ini，初始信息素πj(Ini)(t)=c, 1 ≤j≤n，蚂蚁数量S，目标函数误差Eo等。

2）对蚁群中的S只蚂蚁进行搜索，按式（3）的概率公式随机在集合中选择一条路径，当全部的蚂蚁都到达目标源为止。蚂蚁α(α=1,2,…,S)在Ini中选择j元素的概率为：

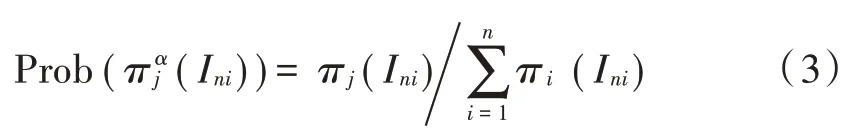
适应度函数与算法效果、评估个体适应度关联密切，结合实际目标优化参数确定适应度函数：适应度函数值非负、唯一值；函数复杂度低；合理、一致性。采用聚类算法效果评测的FMeasure函数定义F=FMeasure作为本算法的适应度函数，F-FMeasure值越小目标函数适应度越低，故将F-FMeasure目标函数转变为最大化问题。

3）构造解空间，更新信息素。从蚁群规模S中随机挑选h数量个体，h=[r⋅S]，r为动态变化选取率；选择群体中信息素浓度最大的个体MAX(πj(Ini))为最优解，蚂蚁i下次行走路径为i=(1-λ)πi(Ini)+λMAX(πj(Ini))，得出当前迭代最优解πj(Ini)best，在蚂蚁i领域局部搜索，寻优规则表达式如下：

式中：δ=0.1⋅rand()，若，公式（5）取“+”，否则为“-”，其中πj(Ini)best⋅0.01，h为动态搜索步长，对应的更新公式为：

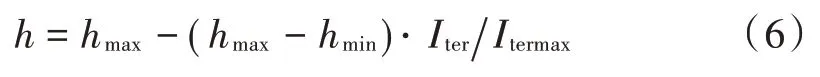
式中：hmax与hmin为预设常量；Iter与Itermax分别为当前迭代次数、最大迭代次数。

当所有的蚂蚁都遍历完集合中的元素后，对路径上的信息更新，选用Ant-Cycle 模型更新信息素，按式（7）进行调整：

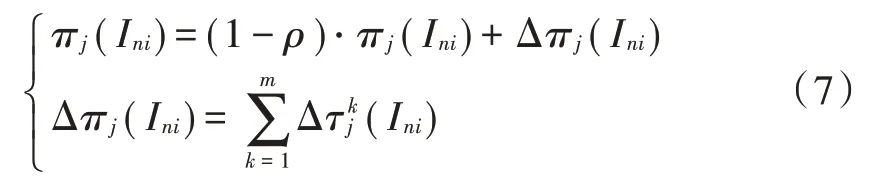
式中：ρ代表信息素挥发系数表示第k只蚂蚁在本次循环集合Ini里的j元素路径上的信息量[10]。

4）对蚁群进行交叉、变异算法操作。交叉算法中选择通用性强的单点交叉（one-point crossover）算子，在序列中随机选择一个交叉点，以这个交叉点为界限，将两个个体染色体结构交叉互换，产生两个新的序列。采用符合高斯算法的正态随机数均值μ、方差σ的正态分布以较小概率改变基因座上的基因值进行变异运算，变异运算主体包括两个元素(x,σ)，x为蚁群下一路径节点，生成新个体表达式为：

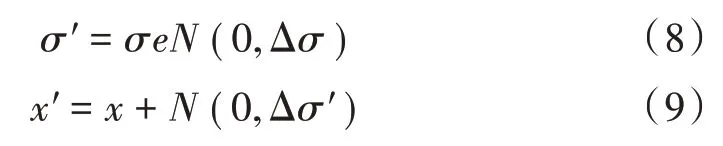
式中：N(0,Δσ′)的均值为0，方差为σ。

根据适应度函数F-FMeasure计算个体适应度，计算每只蚂蚁搜索路径值和时间，判断是否满足当前最优解，若是最优解转入步骤5），否则转入步骤3）。

5）将蚁群算法的寻优结果发送至BP神经网络，计算期望结果与预测结果的误差e。

式中：Oq为期望值；Yq为预测值；q为神经元数量。

6）根据步骤5）的结果，按式（11）～式（14）更新神经网络的权值和阈值：

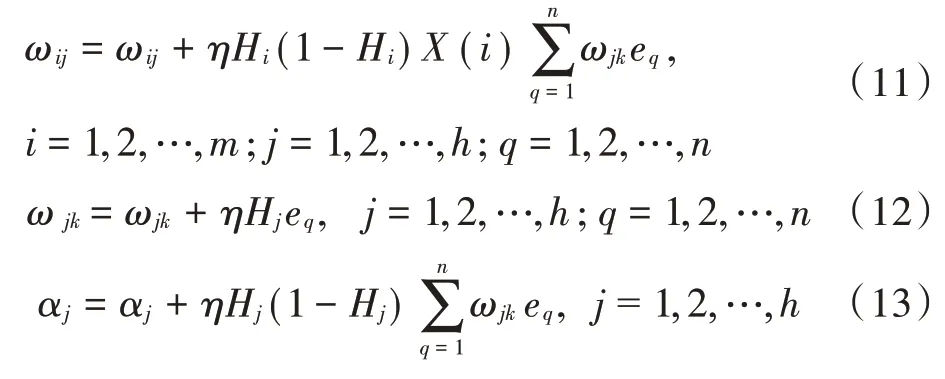
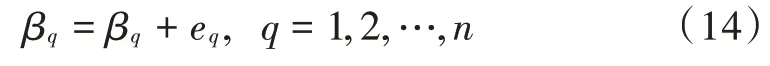
式中：Hi为输入层值；Hj为隐含层值；η为学习率参数。

7）若输出结果的精度满足要求，算法结束，输出最优解，否则转入步骤5）。

4 实验结果及分析

4.1 设置相关参数

为了评价本文GA-ACO-BP 算法性能，选用Matlab R2016a 软件工具对本文算法仿真显示，计算机硬件配置处理器InterⓇCoreTMi5-7300HQ 2.5 GHz，运行内存8.00 GB，64 位操作系统。在目标区域100 m×100 m 范围内随机部署100 个节点，汇聚节点坐标为（0，0），节点初始能量为0.5 J，具体参数定义见表1，GA-ACO-BP 算法的训练在汇聚节点完成，在网络节点用GA-ACO-BP算法对数据融合处理。

表1 实验具体参数Table 1 Specific parameters for experiment

4.2 仿真实验与结果分析

本次仿真结果主要对LEACH，ACO-BP 和GA-ACOBP 三种算法进行网络性能对比，节点能耗对比结果如图4 所示。可以看出，GA-ACO-BP 算法与LEACH 算法、ACO-BP 算法相比，网络能量消耗下降最慢，原因在于ACO 的并行性和正反馈机制结合GA 的快速搜索、全局收敛性，快速找到数据融合移动代理路由，节省能耗；而ACO-BP 算法未在GA 算法中优化，寻优时间较长，融合精度不高。

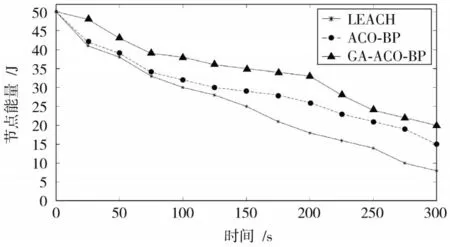
图4 数据融合算法能耗对比Fig.4 Comparison of energy consumption of data fusion algorithms

LEACH 算法基于分布式分簇，簇头的选择不合理和数据融合效果不理想，直接影响到节点能耗，通过图5 可以看出，在大约1 000 轮中节点开始出现死亡，而ACO-BP 算法利用神经网络对数据信息特征提取，融合了部分感知数据，在大约1 200 轮才出现节点死亡，与LEACH 算法相比网络寿命约延长了20%；而GA-ACO-BP算法网络性能最好，有效去除了冗余数据，节点能耗最低，在大约1 350 轮的时候节点出现死亡，与LEACH 算法相比网络寿命约延长了35%，所以它的网络生命周期最长。

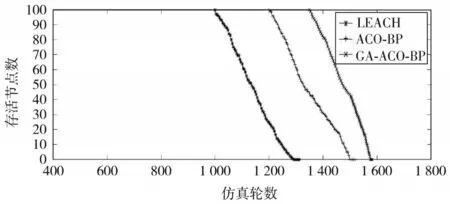
图5 节点生命周期对比Fig.5 Comparison of node life cycles of three algorithms

Sink 节点接收的数据量仿真结果如图6 所示。随着时间的推移，基于LEACH 路由算法存在数据冗余现象，簇头节点过多的数据包造成网络传输堵塞，数据包丢失严重。ACO-BP 算法在一定程度上优化了网络性能，但求解时间长，搜索能力受限，数据融合效果不理想；GA-ACO-BP 算法与ACO-BP 算法、LEACH 算法相比，在Sink 节点接收的数据量最多，这是由于GA-ACOBP 算法对网络性能进行了优化，快速找到全局最优解，改善了BP神经网络数据融合效果，减少数据冗余，降低数据传输延迟，提高了无线信道利用率。

图6 Sink 节点接收数据量Fig.6 Amount of data received by sink node

GA-ACO-BP算法与ACO-BP算法的收敛性对比如图7所示。ACO-BP 算法迭代次数在33 时收敛，GA-ACO-BP算法迭代次数在21 时收敛，显然GA-ACO-BP 算法有着更快的收敛速度，这是因为在蚁群算法中引入遗传算法的交叉算子和变异算子扩大了蚁群算法搜索空间，避免陷入局部最优，提高了蚁群算法的搜索能力和收敛速度。

5 结 语

本文从节省节点能耗，提高网络收集数据的整体效率的目的出发，对WSN 中传感器采集的信息进行数据融合处理，减少了需要传输的数据量。遗传算法搜索最优解来初始化蚁群算法信息素分布，优化后的蚁群算法更新BP神经网络模型的权值和阈值，快速求得目标函数最优解。通过对GA-ACO-BP 算法仿真测试，并与WSN 传统的LEACH 算法和ACO-BP 算法进行综合对比，GA-ACO-BP 算法在收敛速度、降低节点功耗、Sink节点接收的数据量等性能指标方面，都要优于LEACH和ACO-BP 算法，具有一定的应用价值。

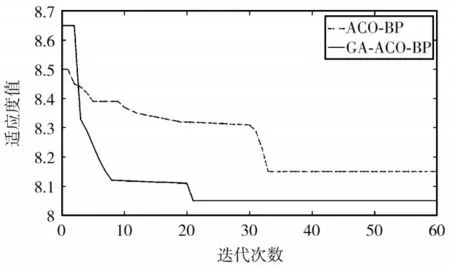
图7 算法迭代对比Fig.7 Iterative comparison of two algorithms