基于部分码字译码的MPA检测算法
张旭宁,葛文萍,刘希腾
(新疆大学信息科学与工程学院,新疆乌鲁木齐 830046)
0 引 言
与第四代移动通信系统相比,第五代(5G)移动通信系统具有广覆盖、低延迟、高可靠、低功耗、高频谱效率和海量连接等特点[1]。由于传统正交多址技术中接入用户数与频谱资源数量成正比,无法满足5G 高频谱效率和海量连接等需求,因此非正交多址接入技术被提出用于解决上述问题[2-4]。针对这一情况,华为提出基于码域的非正交多址接入技术(SCMA),其主要思想是将高维调制和低密度签名多址接入相结合,直接把比特流映射成预先设定码本里的多维码字,从而解决系统过载问题[5]。与正交多址技术相比,SCMA 具有更高的频谱效率和更多的用户接入[6]。然而,将SCMA 应用到5G 系统中还需解决多用户检测复杂度过高的问题。文献[7]提出基于因子图迭代的消息传递算法(MPA)作为SCMA检测的主流算法,其计算复杂度相比最大似然检测明显降低,但是其收敛速度过慢,计算复杂度仍然偏高,因此不适用于实际移动通信系统中。为了提高其收敛速度,文献[8]提出一种串行MPA检测算法。文献[9]根据信道质量,提出一种减少用户节点的MPA 算法;另外,一种基于球形译码的MPA 算法在文献[10]中提出,但该算法只考虑了用户码字在单一资源节点上对检测结果的影响,并未从用户节点的角度考虑码字在多个资源节点上对检测结果的影响。
基于上述分析,本文针对收敛速度较快的串行MPA 算法,提出一种新的基于部分码字球形译码的MPA 多用户检测算法(PCSD-MPA)。该算法综合考虑资源节点和用户间节点之间的映射关系,在原有球形译码算法基础上引入信道质量这一新的判决标准,有效减少了参与迭代的码字,并且由于只有部分码字参与迭代,因此初始化时只对参与迭代的码字进行等概率分配,增大剩余码字的初始概率,加快迭代过程的收敛速率,从而降低检测算法的计算复杂度。
1 系统模型
1.1 上行SCMA 系统模型
在多用户SCMA 系统中,不同用户将输入的二进制比特流通过不同的SCMA 码本,直接映射到SCMA 多维码本的码字上。假设用户数和码本数都是J,每个码本长度为K,非零元素个数为N(N<K),其过载因子定义为在传输时,第j个用户的比特流通过K维复数域码字xj直接映射到K个共享的正交子载波上。其中,码字xj是从码本Xj中选出,且M=|Xj|为码本尺寸。
SCMA 资源块和用户间的映射关系可以用因子图矩阵F=(f1,f2,…,fJ)表示。当且仅当Fkj=1 时,用户节点uj与资源节点rk连接。J=6,K=4 的SCMA 因子图及其矩阵F之间的对应关系如图1 所示。

图1 矩阵F 以及因子图的对应关系Fig.1 Corresponding relationship between matrix F and factor graph
假定一个上行多用户SCMA 通信系统,J个用户共享K个正交时频资源,并传输数据给同一个基站。若所有用户时间同步,基站接收到的信号为所有用户的叠加信号,则接收信号可以表示为:
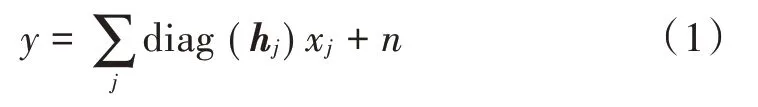
式中:xj表示第j个用户发送的码字;hj表示第j个用户的信道增益向量;n为高斯白噪声,且n~cN(0,σ2I)。则资源节点k处接收到的信号为:

由于码字xj是稀疏的,所以在资源节点k处仅有较少的码字冲突。
1.2 MPA检测算法
MPA 是SCMA 检测的主流算法,其实现过程包括两个阶段:
阶段1:所有资源节点以用户节点传递过来的信息为先验信息,同时更新因子图中全部资源节点rk到用户节点uj的消息
阶段2:所有用户节点通过合成资源节点传递过来的消息进行更新,同时更新因子图中所有用户节点uj到资源节点rk的消息则MPA 可以用数学公式表示为:

式中:t为迭代次数;εk与ζj分别表示稀疏码矩阵F第k行的非零位置集与第j列的非零位置集。其中,概率密度函数为:

式中:xk([mj])定义为资源块k上所连接的所有用户发送端可能发送的码字元素组成集合,达到预先设定的最大迭代次数tmax后,用户码字输出概率可以表示为:

为了有效提升MPA 算法的收敛速度,文献[10]提出了串行MPA 算法,其表达式如下:
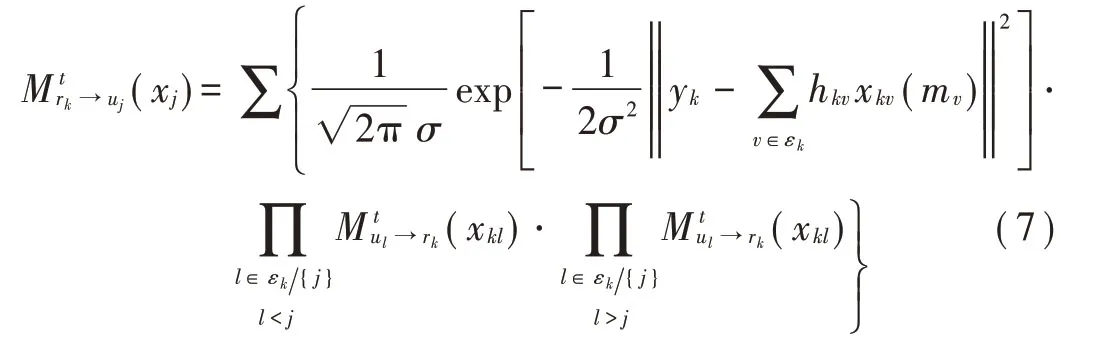
串行MPA 多用户检测算法在每轮迭代过程中,更新后的消息马上传递给后续节点,而不必等到下一轮迭代过程,加快了MPA 的收敛性。 串行MPA(3 次迭代)和MPA(6 次迭代)达到收敛后的性能相当,但其计算复杂度依然偏高,仍有较大改进空间。
2 PCSD-MPA检测算法
为了进一步降低MPA 的复杂度,本文结合SCMA 的非正交性,以球形译码理论为基础,引入信道质量这一新的判决标准,对用户码字进行筛选,减少参与迭代的码字从而降低MPA 的计算复杂度。假定J=6,K=4,式(2)按因子图矩阵F展开得:
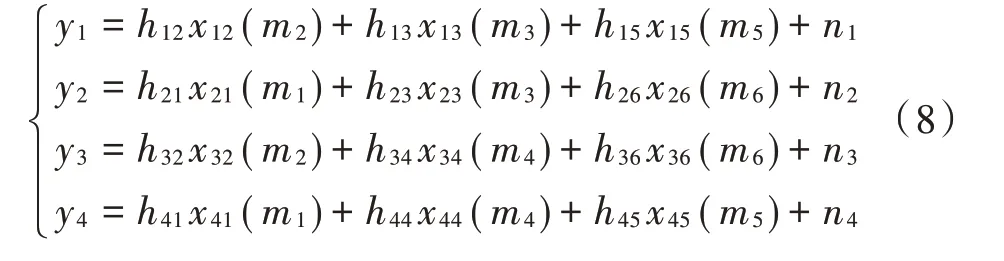
当码本尺寸M=4 时,由式(8)可知,资源节点rk上所承载的用户数df=3,则资源节点k上有43=64 个合成星座点(Synthetic Constellation Points,SCP)参与MPA 迭代运算,其分布如图2 所示。

图2 一个资源节点上SCP 的分布Fig.2 Distribution of received signal point and SCPs at one RN
由球形译码理论可知,合成星座点的欧氏距离越接近接收信号点,越有可能正确译码[10]。则可以通过设置球形半径来减少参与迭代的用户码字,其表达式为:
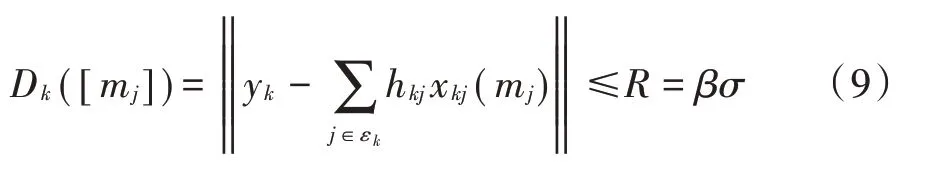
式中:Dk([mj])为合成星座点与接收信号之间的欧氏距离;β是大于0的实数。当Dk([mj])大于半径R时,舍弃对应的SCP,仅保留Dk([mj])小于半径R的这一部分码字参与MPA 的计算。球形译码半径R是由噪声功率σ2决定的,通过调节R的大小可以在计算复杂度和误码率(Bit Error Ratio,BER)之间取得折中。其中,β=1,2,3 时的置信区间和正确译码概率之间的对应关系如表1所示。
当R=2σ时,置信区间为(-2σ,2σ),可以保证资源块k上正确译码的概率值达到95.4%。
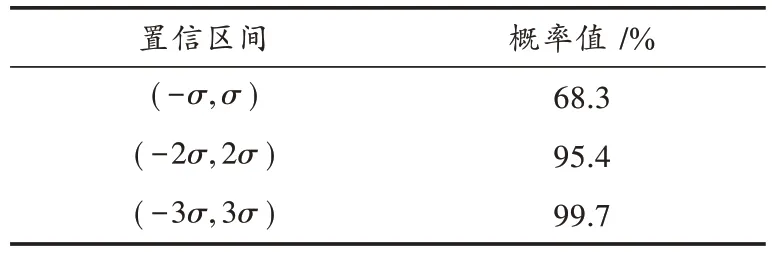
表1 正态分布规律Table 1 Principles of normal distribution
通过式(9)将筛选后的码字代入式(3),则式(3)可以改写为:
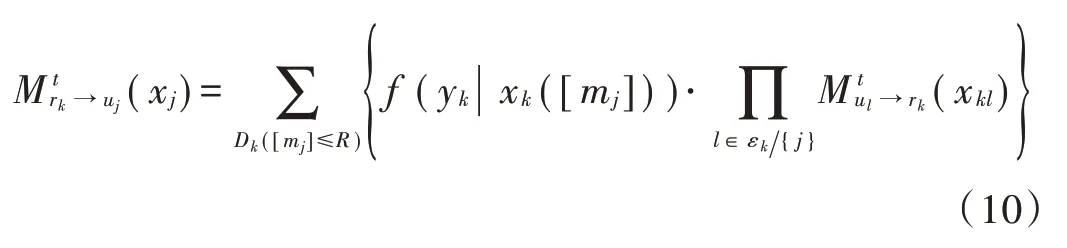
式中:半径R值设定要合理,过小将会把一部分能够正确译码的码字筛选掉,从而影响检测结果。该式即为文献[10]提出的SD-MPA 多用户检测算法,可以明显降低算法复杂度。但该算法只考虑了用户码字对资源节点译码的影响,并未考虑对用户节点的影响。从用户节点考虑,假设第j个用户的码字xj(mj)中的N个非零元素xnj(mj)(1 ≤n≤N)同时映射到了N个资源节点上,那么在同一球形半径R的条件下,第n个资源节点上满足门限条件的合成星座点将会包含j用户的码字元素xnj(mj)。由于信道为独立衰落信道,du个信道系数hk,j(k∈ζj) 都不相同,即一些资源节点的信道增益比其他资源节点大得多,信道质量越高,通过该信道的消息越可靠,因此可以将信道质量作为码字筛选的一个评判标准。本文采用华为公布的4~6 码本,每个用户占用两个资源进行数据传输。让k1和k2分别代表每个码字中的两个非零元素的位置,则码字筛选公式定义如下:
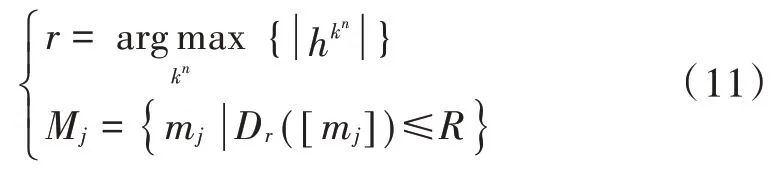
式中M j表示用户j的候选码字集合,只有信道质量最佳的资源节点用来筛选用户j的码字。将由式(11)得到的候选码字代入式(7),则式(7)可以改写为:

式(12)即为本文提出的PCSD-MPA 多用户检测算法,该算法由于综合考虑了资源节点和用户节点之间的数据映射关系,不但减轻资源节点的负担,还能减轻用户节点的负担,且该算法只有部分码字参与多用户检测阶段,对初始化时,只对参与运算的码字等概率分配,初始化公式定义为:

由式(13)可知,由于采用部分码字初始概率均等分配策略,剩余码字越少,每个码字的初始概率越大,这样可以加快迭代的收敛速度,有效降低了计算复杂度。
3 仿真结果分析
本文基于典型的上行SCMA 系统模型对提出的PCSD-MPA 进行仿真,并与串行MPA 和SD-MPA 算法进行比较,具体仿真参数如表2 所示。

表2 仿真参数Table 2 Simulation parameters
3.1 误码率性能对比
图3 为本文提出的PCSD-MPA 与串行MPA 以及SD-MPA 在迭代3 次的误码率性能随信噪比(Signal to Noise Ratio,SNR)的对比图。由图3 可以看出,判决半径R越小,BER 性能越差,原因是R过小将会过度筛选用户码字信息。当R=2σ时,本文所提到的三种算法的误码率性能相近,主要原因是基于欧氏距离的球形译码理论进行码字筛选可以大概率的保证多用户检测的正确性。
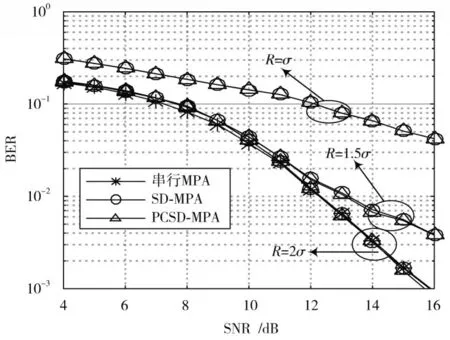
图3 不同R 下的BER-SNR 性能比较Fig.3 Comparison of BER performance at different R
3.2 收敛性能对比
图4 为本文所提PCSD-MPA(R=2σ)与SD-MPA(R=2σ)以及串行MPA 收敛性对比图。由图4 可知,本文所提算法在高SNR 条件下,迭代1 次和2 次的BER 性能要好于SD-MPA 和串行MPA 算法。SD-MPA 在迭代次数较小的情况下其误码率性能与串行MPA 接近。值得注意的是,本文所提算法,迭代2 次的BER 性能与串行MPA 迭代3 次的BER 性能接近,原因是高信噪比条件下筛选掉的码字较多,这样在初始化阶段采用部分码字概率均等策略可以加快其收敛速度。
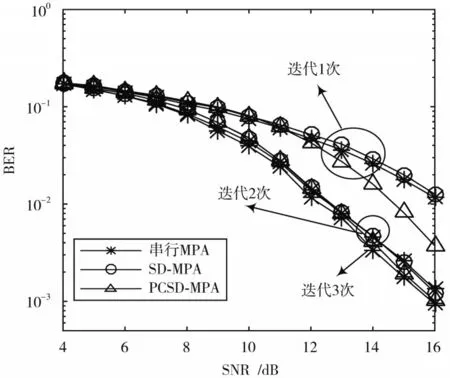
图4 收敛性对比Fig.4 Comparison of convergence behaviors
3.3 复杂度对比
图5 表示本文所提算法PCSD-MPA、SD-MPA 以及串行MPA 在tmax=3 时算法复杂度对比。算法复杂度以任意资源节点k处平均合成星座点传递量进行衡量,串行MPA 算法每个资源节点的平均合成星座传递量为64。由图5 可知,SD-MPA 随着R的减少复杂度越来越低。本文所提算法复杂度呈现快速下降趋势,复杂度进一步降低,原因是根据SCMA 的非正交特性,引入信道质量这一新的判决机制,进一步去掉了一些合成星座点,因此能有效降低复杂度。综合来看,本文所提算法在误码率性能和复杂度之间能够取得较好的平衡。

图5 复杂度对比Fig.5 Comparison of complexity
4 结 语
本文针对MPA 具有复杂度较高的特点,根据球形译码理论,结合SCMA 的非正交特性,提出一种基于部分码字球形译码运算的PCSD-MPA 多用户检测算法。由于每个用户只有部分码字参与检测阶段,在初始化阶段,采用部分码字初始概率均等分配策略,因此有助于提升其收敛性。仿真结果表明,相比串行MPA,在球形半径设定合理的情况下,本文所提的PCSD-MPA 可以在复杂度和误码率之间取得较好的平衡,且在SNR 较高的条件下,收敛速度也有所提高,更适用于5G 通信系统。

