基于改进型Kriging-HDMR的翼身融合水下滑翔机外形优化设计
张 宁, 王 鹏, 宋保维
基于改进型Kriging-HDMR的翼身融合水下滑翔机外形优化设计
张 宁, 王 鹏, 宋保维
(西北工业大学 航海学院, 陕西 西安, 710072)
为了使翼身融合水下滑翔机(BWBUG)具有更优的升阻特性, 文中通过在优化过程中引入改善期望(EI)补点策略和移动中心点策略, 对传统克里金-高维模型表示(Kriging-HDMR)优化方法进行了改进, 以达到更准确的预测精度和更高效的优化效率。首先通过基于分类函数变换的参数化方法, 建立BWBUG外形的参数化模型, 然后以最大化升阻比为优化目标, 采用改进型Kriging-HDMR优化方法, 对BWBUG外形进行优化设计。试验结果表明, 优化后BWBUG外形的升阻比比初始外形提高了3.135 6%。
翼身融合水下滑翔机; 克里金-高维模型表示; 外形优化; 改善期望
0 引言
翼身融合水下滑翔机(blended-wing-body un- derwater glider, BWBUG)作为一种新型水下滑翔机, 其搭载能力强、能源利用率高、噪声性能好, 应用前景十分广泛。通常来说, 水下滑翔机升阻比越高, 滑翔效率越高。因此在水下滑翔机外形优化设计过程中, 常将升阻比作为优化目标[1-2]。
在实际优化过程中, 使用传统计算流体动力学(computational fluid dynamics, CFD)方法计算水下滑翔机不同外形条件下的升阻比, 存在优化时间长、计算代价高、仿真模型调用次数多等问题。为此, 使用代理模型优化方法对水下滑翔机外形参数进行基于仿真的优化已成为趋势, 该方法通过代理模型代替昂贵的流体仿真计算, 能够有效地减少仿真模型的调用次数[3-6]。然而, 随着优化问题复杂度和维数的增加, 构建代理模型所需采样点数量和计算成本会以指数方式增长, 且难以达到满意的预测准确度, 这就迫切需要一种能够精确对高维非线性问题建模的近似方法。高维模型表示(high dimensional model representation, HDMR)就是一种处理高维贵重黑箱问题的有效方法。
文中在对BWBUG的3个关键截面参数化建模的基础上, 以最大化升阻比为目标, 对其外形进行优化设计, 提出一种基于克里金-高维模型表示(Kriging-HDMR)的水下滑翔机外形优化方法, 该方法使用移动中心点策略提高了模型预测精度, 同时利用改善期望(expected improvement, EI)补点策略加强了补充样本点的质量。数值算例和优化结果表明, 该方法对高维贵重黑箱问题具有很好的适用性和稳定性。
1 基于Kriging-HDMR的代理模型优化方法
1.1 HDMR概述
HDMR是一种用来解决高维问题的近似模型, 其一般表达式为


HDMR主要有2种形式: ANOVA(analysis of variance)-HDMR和Cut-HDMR。前者主要用于灵敏度分析和确定关键设计变量, 后者由于计算效率高、无需计算梯度信息等优点被广泛应用于预测高维贵重黑箱问题[7-10]。Cut-HDMR也有多种形式, 例如: Kriging-HDMR、RBF(radial basis fu- nction)-HDMR、SVR(support vector regression)- HDMR以及MLS(moving least square)-HDMR。以Kriging- HDMR为例构建对应模型的主要过程如下。

3) 在维设计变量的取值范围内随机选取1个新的采样点, 验证f(x)是否收敛。若收敛则f(x)项构建完成; 否则用当前项所有采样点构建新的Kriging代理模型, 循环步骤3)直到达到收敛条件。
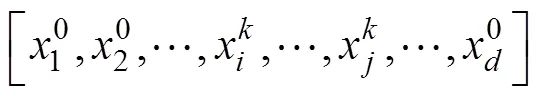
1.2 Kriging-HDMR优化方法
Kriging模型是一种基于误差相关性的无偏估计方法, 它不仅可以给出未知样本处响应值, 还可以预测样本处的不确定性, 在代理模型优化方法中被广泛使用。Kriging-HDMR是将Kriging代理模型与HDMR方法相结合, 在近似高维非线性问题时十分有效, 因此被应用于诸多实际工程优化问题[11-13]。然而当前Kriging-HDMR方法在处理高维优化问题时存在一定缺陷, 如对高维贵重问题计算代价较大、优化结果难以满足要求、随机选取采样点导致预测精度低等。为了进一步提高建模效率和预测精度, 文中提出了一种改进型Kriging-HDMR代理模型优化方法。
针对建模过程中随机选取采样点导致预测精度低的问题, 在代理模型构建中使用EI补点策略代替随机补点策略[14], 该策略可以很好地平衡优化过程中的局部开发能力与全局探索能力, 避免搜索过程陷入到局部最优解; 同时, 在优化过程中随着迭代次数增加, 最优点范围往往确定在某一区域, 如果将HDMR方法中的中心点设置成随优化进行不断趋近于最优点, 无疑可以增加最优点附近代理模型的准确度, 提高优化效率, 从而进一步提升最终优化结果, 因此使用移动中心点策略代替固定中心点策略; 最后选取灰狼算法[15]作为Kriging-HDMR方法优化过程中的全局优化算法。
Kriging-HDMR优化方法的流程如图1所示, 具体步骤如下。
2) 从第1维设计变量开始构建Kriging- HDMR模型: 首先构建该维设计变量的非耦合项(1阶项), 根据初始采样点建立Kriging代理模型, 然后根据EI补点策略向当前项采样集中加点直到满足数量要求, 使用当前项采样集中所有采样点建立当前非耦合项Kriging代理模型; 使用相同方法构建该维设计变量与目前已经建模完成的设计变量相关的所有1阶耦合项(2阶项)Kriging代理模型。
3) 通过灰狼算法对当前不完全Kriging- HDMR模型进行优化, 得最优解从而生成新的中心点, 使用新中心点通过步骤2)中所描述方法构建下一维设计变量的非耦合项及1阶耦合项模型。
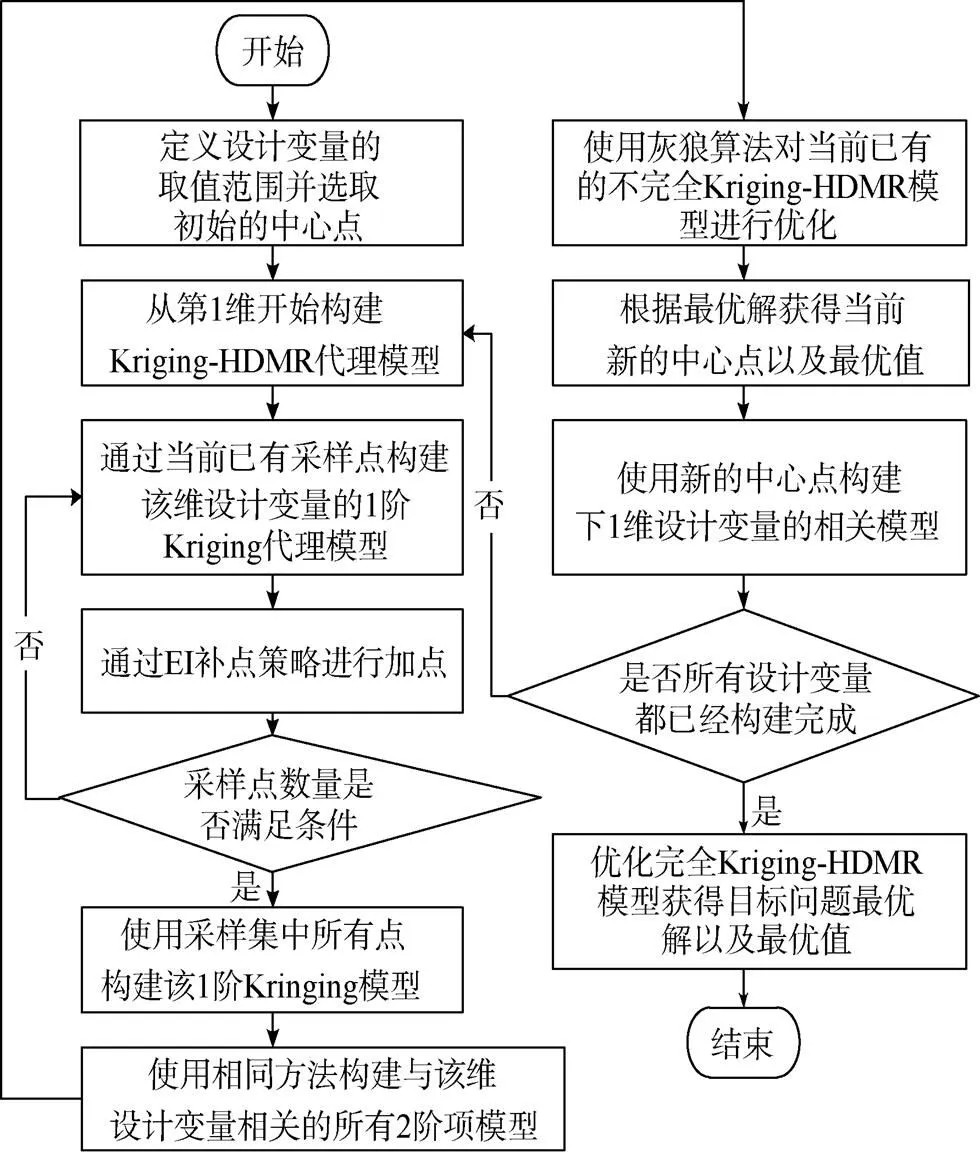
图1 克里金-高维模型表示优化方法流程图
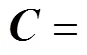

5) 重复上述步骤直到所有设计变量都已建模完成, 得到最终Kriging-HDMR完整模型, 优化该模型得到目标问题的最优解以及最小值点。
1.3 数值算例与验证


表1 测试函数列表
图2给出了2种方法针对数值算例的优化过程, 从图2可知, 文中所提Kriging-HDMR优化方法在所有测试函数中均能以更快速度逼近最优解。
表2 给出了2种方法的最终优化结果。由表中可知, 2种方法在Sphere函数、Alpine函数、Rastrigin函数及Powell函数找到的最优解值与实际值很接近, 而文中的Kriging-HDMR优化方法在所有测试问题上的表现更好。由上述结果可以得出, 文中提出的Kriging-HDMR优化算法整体优势比较明显, 不仅在迭代过程中寻优速度较快, 而且最终可以得到比较理想的优化结果。
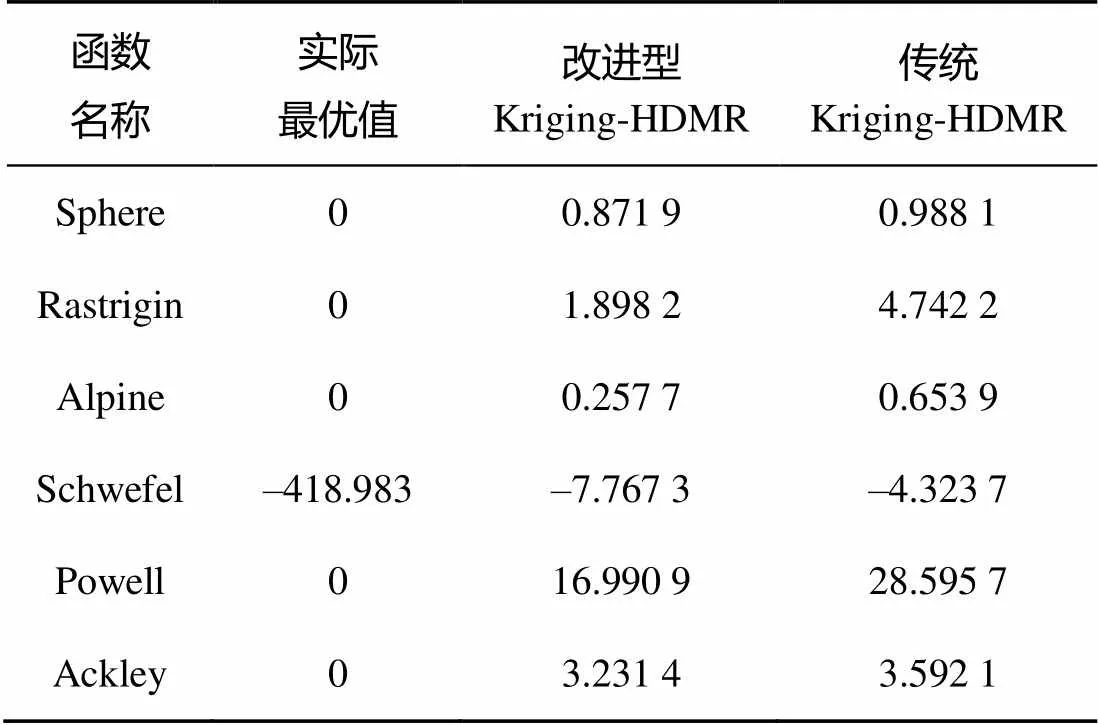
表2 测试函数优化结果比较

图2 测试函数迭代过程比较
2 BWBUG外形优化设计
2.1 问题描述
BWBUG平面形状如图3所示, 其外形主要由3个关键截面构成, 分别选择NACA0022、NACA0016、NACA0010作为、、各截面的基础翼型, 各平面几何参数取值如表3所示。

图3 翼身融合水下滑翔机平面形状图

表3 BWBUG平面几何参数值
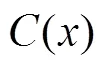


为了保证最终优化结果的准确性, 将设计变量的取值范围映射为与基础翼型相近的2个翼型之间, 其中截面被限定在标准翼型NACA0028和NACA0016之间, 截面被限定在标准翼型NACA0022和NACA0010之间, 截面被限定在标准翼型NACA0012和NACA0008之间。最终优化问题可以表示为


优化方法伪代码如下表示:
Begin
通过CST方法对水下滑翔机外形进行参数化建模, 并针对该优化问题归纳出21个设计变量;
淖尔水质超标物主要有pH值、全盐量、氯化物和硬度,盐分处于主导地位。根据农田灌溉水质要求和滴灌工程设计要求,降低盐分和抗堵塞是淖尔水质处理的关键。考虑灌溉的低成本和实效性要求,水源处以分凌水或引黄灌溉水与淖尔蓄水量按一定比例混合稀释,以降低淖尔盐分含量。首部采用泵前低压网式过滤器+叠片过滤器组合模式,田间采用抗堵型内镶贴片式灌水器可实现低成本高效过滤。
初始化优化问题设计空间和Kriging-HDMR优化算法中心点, 设置灰狼算法的初始化参数;
For= 1 :(21)
使用EI策略生成采样点;
通过采样点构建当前维设计变量的非耦合项模型;
通过相同方法构建与当前维设计变量相关的1阶耦合项模型;
采用灰狼算法获得当前不完全Kriging- HDMR代理模型的最优解;
将当前最优解作为新的中心点进行下一轮迭代;
End
通过灰狼算法对完整Kriging-HDMR模型进行优化并得到最优解;
通过最优解获得优化后翼型以及升阻比;
End
2.2 优化结果与分析
从表4可知, 通过文中所提Kriging-HDMR优化方法优化后的滑翔机外形升阻比比初始设计提高了3.1356%, 这一数值明显高于传统Kriging- HDMR优化方法的2.0822%。
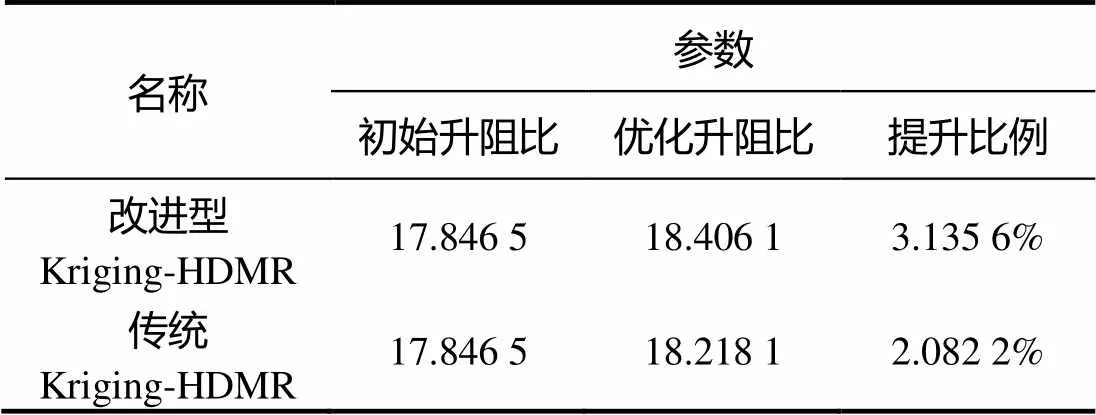
表4 BWBUG外形升阻比优化结果比较
图4为2种方法优化迭代过程收敛图, 可以看出, 改进型Kriging-HDMR优化方法能够更快速地逼近最优解并达到很好的优化结果。

图4 BWBUG外形升阻比迭代过程比较
图5为初始剖面翼型和改进型Kriging- HDMR优化后剖面翼型对比。图5将经过文中提出的改进型Kriging-HDMR优化方法优化后的滑翔机翼型进行参数化, 得到优化前后3个剖面翼型对比。
图6为优化前后滑翔机压力分布对比, 从图中可以看出, 优化后水下滑翔机翼身在下表面多数区域的压力要明显高于初始翼身下表面压力, 同时在上表面也存在类似情况, 从而使优化后的BWBUG获得了更大的升阻比。
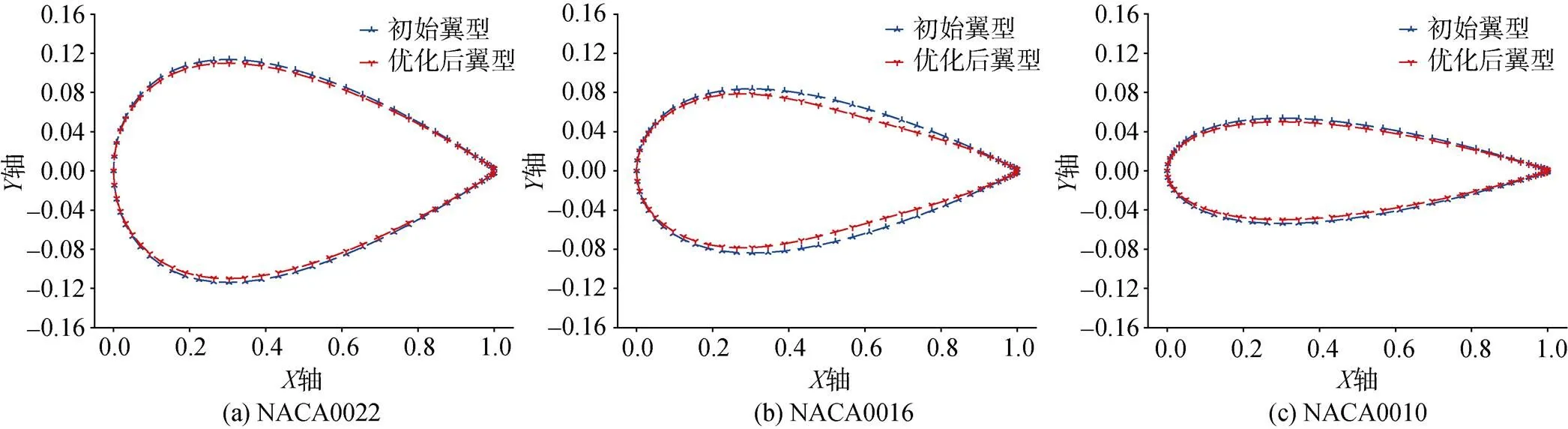
图5 初始剖面翼型和改进型Kriging-HDMR优化后剖面翼型对比
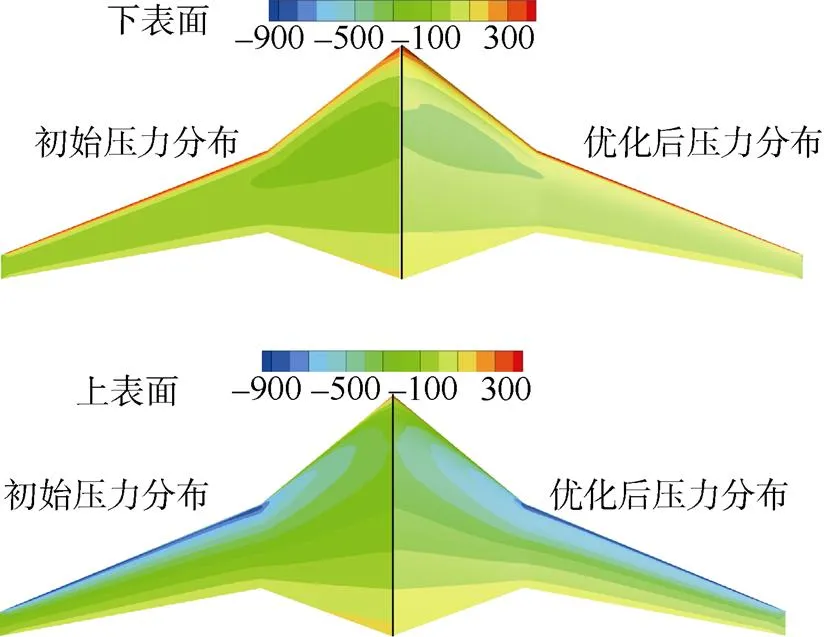
图6 表面初始压力分布云图和改进型Kriging-HDMR优化后压力云图对比
3 结束语
文中针对BWBUG外形优化问题, 通过在传统Kriging-HDMR优化方法中加入EI补点策略以及移动中心点策略, 提出了一种改进型Kriging- HDMR优化方法, 并在多个数值算例上进行了对比验证, 结果表明, 文中所提出的优化方法可以更加快速稳定地逼近最优解并能得到较好的优化结果。在此基础上, 以最大化升阻比为目标, 采用改进型Kriging-HDMR优化方法对BWBUG外形进行优化设计, 优化结果显示, BWBUG外形的升阻比有了明显提高。
[1] 谷海涛, 林扬, 胡志强, 等. 基于代理模型的水下滑翔机机翼设计优化方法[J]. 机械工程学报, 2009, 45(12): 7-14.Gu Hai-tao, Lin Yang, Hu Zhi-qiang, et al. Surrogate Models Based Optimization Methods for the Design of Underwater Glider Wing[J]. Journal of Mechanical Engineering, 2009, 45(12): 7-14.
[2] Sun C, Song B, Wang P. Parametric Geometric Model and Shape Optimization of an Underwater Glider with Blended-wing-body[J]. International Journal of Naval Architecture & Ocean Engineering, 2015, 7(6): 995- 1006.
[3] Box G E P, Draper N R. Empirical Model-building and Response Surfaces[M]. Hoboken, NJ: John Wiley & Sons, 1987.
[4] Fang H, Horstemeyer M F. Global Response Approxim- ation with Radial Basis Functions[J]. Engineering Opti- mization, 2006, 38(4): 407-424.
[5] Cressie N. Spatial Prediction and Ordinary Kriging[J]. Mathematical Geology, 1988, 20(4): 405-421.
[6] Smola A J, Schölkopf B. A Tutorial on Support Vector Re- gression[J]. Statistics and Computing, 2004, 14(3): 199- 222.
[7] Shan S, Wang G G. Survey of Modeling and Optimization Strategies to Solve High-dimensional Design Problems with Computationally-expensive Black-box Functions[J]. Structural and Multidisciplinary Optimization, 2010, 41(2): 219-241.
[8] Shan S, Wang G G. Turning Black-box Functions into White Functions[J]. Journal of Mechanical Design, 2011, 133(3): 031003-1-031003-10.
[9] Cai X, Qiu H, Gao L, et al. An Enhanced RBF-HDMR Integrated with an Adaptive Sampling Method for App- roximating High Dimensional Problems in Engineering design[J]. Structural and Multidisciplinary Optimization, 2016, 53(6): 1209-1229.
[10] Chen L, Wang H, Ye F, et al. Comparative Study of HDMRs and Other Popular Metamodeling Techniques for High Dimensional Problems[J]. Structural and Multidisciplinary Optimization, 2019, 59(1): 21-42.
[11] 汤龙, 李光耀, 王琥. Kriging-HDMR非线性近似模型方法[J]. 力学学报, 2011, 43(4): 780-784. Tang Long, Li Guang-yao, Wang Hu. Kriging-HDMR Me- tamodeling Technique for Nonlinear Problems[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(4): 780-784.
[12] Chen L, Li E, Wang H. Time-based Reflow Soldering Optimization by Using Adaptive Kriging-HDMR method[J]. Soldering & Surface Mount Technology, 2016, 28(2): 101-113.
[13] Wu X, Peng X, Chen W, et al. A Developed Surrogate-Based Optimization Framework Combining HDMR-Based Modeling Technique and TLBO Algorithm for High-dimensional Engineering Problems[J]. Structural and Multidisciplinary Optimization, 2019, 60(2): 663-680.
[14] Jones D R, Schonlau M, Welch W J. Efficient Global Optimization of Expensive Black-box Functions[J]. Journal of Global optimization, 1998, 13(4): 455-492.
[15] Mirjalili S, Mirjalili S M, Lewis A. Grey Wolf Optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61.
Shape Optimization for Blended-Wing-Body Underwater Glider Using Improved Kriging-HDMR
ZHANG Ning, WANG Peng, SONG Bao-wei
(School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)
To make the shape of blended-wing-body underwater glider(BWBUG) have better lift and drag characteristics, an advanced surrogate-based optimization method using a Kriging-high dimensional model representation(Kriging- HDMR) is presented. In this algorithm, expected improvement(EI) criterion and moving cut point are employed during optimization process to improve the accuracy and efficiency of the optimization. Class-shape function transformation(CST) method is used to establish a parameterization model for the shape of BWBUG. Then, in order to maximize the lift-to-drag ratio, the improved Kriging-HDMR method is used to optimize the shape of BWBUG. The results show that the lift-to-drag ratio of the BWBUG shape is improved by 3.135 6% with the proposed HDMR optimization method.
blended-wing-body underwater glider(BWBUG); Kriging-high dimensional model representation(HDMR); shape optimization; expected improvement(EI)
TJ630.2; U674.941; TP18
A
2096-3920(2019)05-0496-07
10.11993/j.issn.2096-3920.2019.05.004
张宁, 王鹏, 宋保维. 基于改进型Kriging-HDMR的翼身融合水下滑翔机外形优化设计[J]. 水下无人系统学报, 2019, 27(5): 496-502.
2019-05-15;
2019-06-03.
国家自然科学资金项目资助(51875466, 51805436).
张 宁(1989-), 男, 在读博士, 主要研究方向为高维代理模型优化.
(责任编辑: 杨力军)

