Petrel-II 200水下滑翔机动力学建模及仿真

孙秀军, 王 雷, 桑宏强

Petrel-II 200水下滑翔机动力学建模及仿真

孙秀军1,2,3, 王 雷1, 桑宏强4

(1. 河北工业大学 机械工程学院, 天津, 300130; 2. 中国海洋大学 物理海洋教育部重点实验室, 山东 青岛, 266100; 3. 青岛海洋科学与技术试点国家实验室 海洋动力过程与气候功能实验室, 山东 青岛, 266237; 4. 天津工业大学 机械工程学院, 天津, 300387)

国内对水下滑翔机动力学行为的研究多针对深海型及横滚转向机制, 而对浅海型、尾舵转向类型研究较少。基于此, 文中以Petrel-II 200浅海型水下滑翔机作为模型进行动力学建模及运动仿真分析, 并引入海流等干扰因素, 为浅海型水下滑翔机的运动形式提供参考。根据Petrel-II 200三维模型中各质量的相对运动关系将其质心简化为由多个质点组成的多刚体系统, 构造质心与质点之间的关系式; 基于动量及动量矩定理对Petrel-II 200进行动力学分析, 对水下滑翔机所受重力、驱动浮力以及水动力进行体坐标系转换, 并推算出完整的动力学方程, 明确了升阻比与回转半径表达式; 通过选取水下滑翔机物理、水动力学参数, 对锯齿、螺旋等典型运动进行仿真试验。该仿真结果验证了动力学模型的准确性和可靠性, 为后续Petrel-II 200水下滑翔机的运动性能优化和控制算法设计提供了良好的仿真平台。

水下滑翔机; 动力学建模; 动力学方程; 运动仿真

0 引言

水下滑翔机是一款不需要外挂推进系统的自主航行观测设备, 因其耗能低、跨度大等优点, 可用来实现长期海洋观测。针对水下滑翔机下潜深度及应用场合不同可将之划分为深海型与浅海型, 两者各有特点、优势互补, 具有不同的海洋观测应用范围。深海型水下滑翔机工作于水下几千米的环境, 通过微小浮力变化及内置姿态调节机构实现滑翔运动, 单次剖面测量耗能较少, 续航能力强, 是目前较为常见、研究较多的一类。

为了对近浅海及其温跃层的海洋动力、水质生态以及海洋声学等进行深入地观测研究, 美国Woods Hole海洋研究所研制了Slocum 200浅海型水下滑翔机,相比于Spray、Seaglider等通过旋转内部质量模块来改变整体姿态, 从而进行螺旋转向的深海型水下滑翔机, 浅海型水下滑翔机采用尾舵转向机构进行螺旋回转, 省去了由横滚调节至合适姿态所需时间, 在较短的下潜深度内快速完成回转操作, 使其具有较高的机动性[1]。另外, 浅海型水下滑翔机相对于深海型设计有更大的浮力调节量, 有较快的滑翔速度来克服部分海流的干扰。2012年初, 天津大学、中国海洋大学、天津工业大学等单位, 共同研制了200 m额定潜深的Petrel-II 200水下滑翔机, 如今已完成样机试制并开展海上应用。

为了对Petrel-II 200水下滑翔机进行优化设计指导及性能评估, 需要进行动力学建模与参数识别。目前, 世界各国对水下滑翔机的动力学研究已取得显著的成果。Leonard[2-3]通过控制水下滑翔机样机模型的重心位置得到了相应的滑翔轨迹, 利用几何关系及动力学理论对水下滑翔机进行了动力学分析, 开创了水下滑翔机理论研究的先河; 俞建成[4]、王长涛[5]和Zhang[6]等, 基于牛顿-欧拉方程建立了水下滑翔机系统的动力学模型, 利用水动力软件进行了运动参数辨识; 王树新[7]、武建国[8]、孙秀军[9-11]、Niu[12]和王延辉[13]等, 利用浮基多刚体理论和鱼雷水动力模型建立了水下滑翔机的动力学方程, 并利用吉布斯-阿佩尔方程对非线性动力学方程的精确性做了进一步的提升[13]; 温浩然等[14]对水下滑翔机的优化设计、研制进行了深入研究。

但上述成果多针对深海型、横滚转向的水下滑翔机进行动力学行为研究, 而对浅海型、尾舵转向的水下滑翔机动力学行为研究较少。基于此, 文中以Petrel-II 200浅海型水下滑翔机作为模型进行动力学建模及运动仿真分析, 并引入了海流的干扰因素, 为浅海型水下滑翔机的运动形式提供参考。

1 Petrel-II 200空间运动

1.1 坐标系及运动参数定义

根据文献[15], 建立Petrel-II 200大地坐标系(地系)、体坐标系(体系)与速度坐标系(速系), 如图1所示。体系与水下滑翔机机体固连, 以排水浮心作为体系坐标原点,轴沿机身纵轴向前,轴重合于机翼平面向右,轴指向机身腹部, 文中其他参数定义参见表1。

体系到地系的转换矩阵

同理, 速度坐标系到体坐标系的转换矩阵

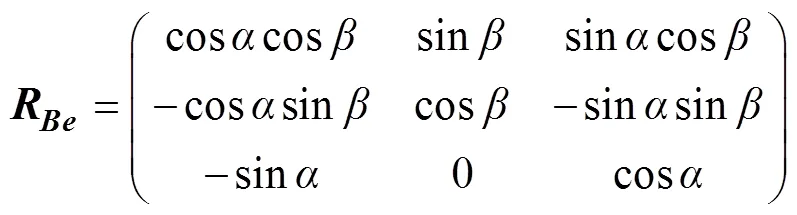
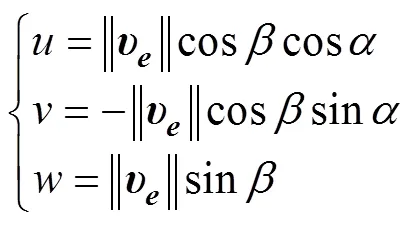
表1 Petrel-II 200运动参数

1.2 Petrel-II 200运动学方程

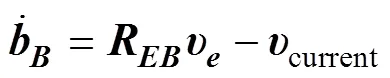
体系下的姿态可以描述为

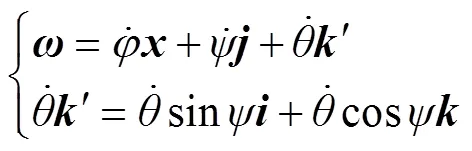
联立式(1)、式(4)、式(5)和式(6)可得Petrel-II 200的运动学方程为

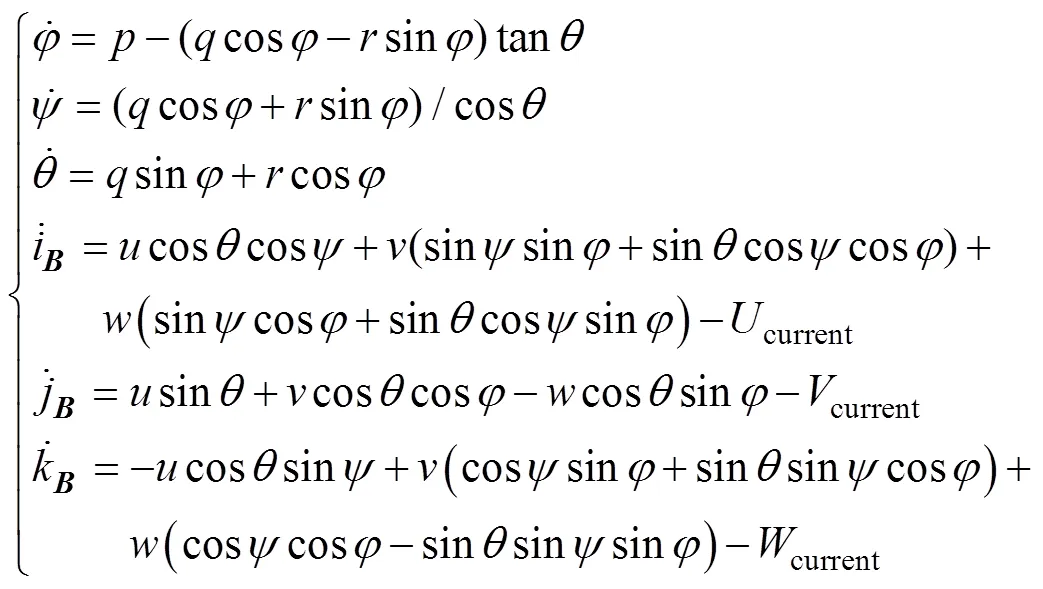
2 Petrel-II 200动力学建模

2.1 Petrel-II 200等效质量处理

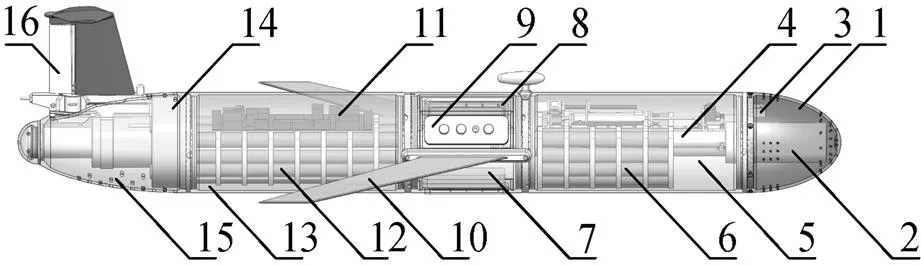
1-导流罩 2-浮力调节模块 3-电子罗盘 4-液压系统 5-前舱段 6-俯仰调节模块 7-压舱块 8-中舱段 9-外接接口 10-机翼 11-信号电源管理电路 12-尾部配重电源 13-后舱段 14-传感器模块 15-尾部导流罩 16-尾舵系统

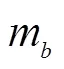
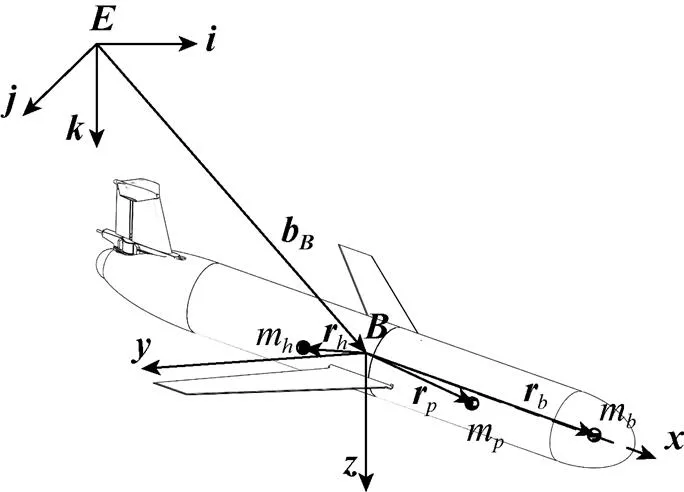
图3 质量模型简化示意图

质心处的矢径

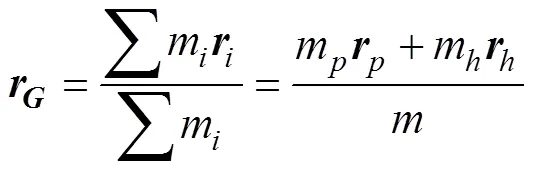
质心与质点系的坐标关系为

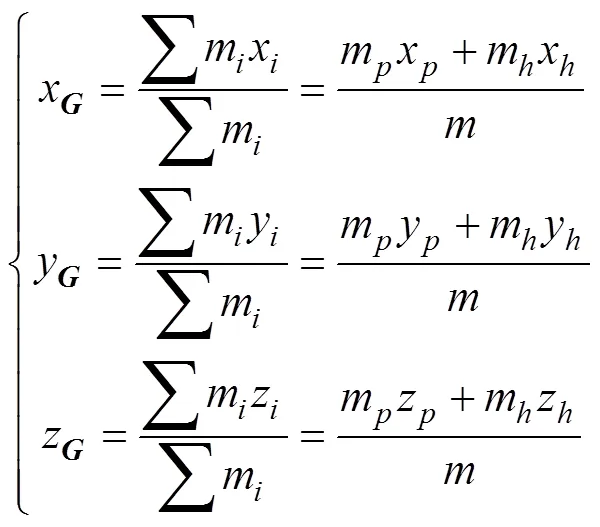
2.2 动力学方程

根据运动学理论, 水下滑翔机质心相对于浮心的运动速度为

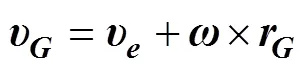
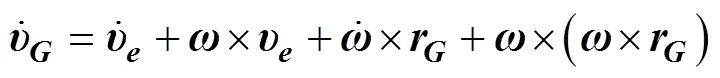
由刚体的转动定律可知, 质心处的角动量

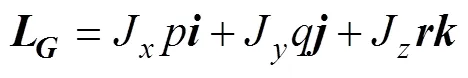
式中: J表示质心对体系各轴的转动惯量, 且=,,。

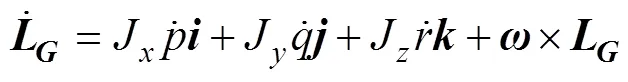
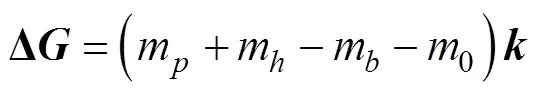
水下滑翔机在水中运动时会受到净浮力、水动力和水动力矩的作用, 其中水动力又分为粘性水动力和惯性水动力, 对体坐标系下质心处进行受力分析, 有

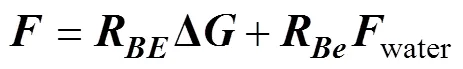
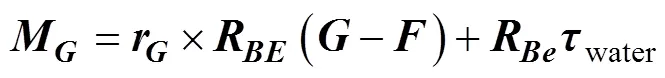
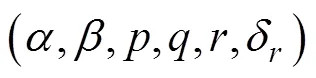
Petrel-II 200做横向运动或转动时, 由加速运动引起的惯性水动力与加速度、角加速度成线性关系, 根据势流理论, 在流体中产生的附加质量为

根据动量及动量矩定理可知, 水下滑翔机质心处动量与角动量随时间的变化率与质心所受合外力与合外力矩有以下关系

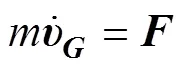
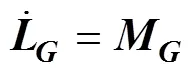
联立式(8)~(20)可得Petrel-II 200的动力学方程

2.3 运动性能分析

如图4所示, 水下滑翔机进行锯齿形操作时只做垂向剖面运动, 不做横向运动, 水下滑翔机的速度大小为

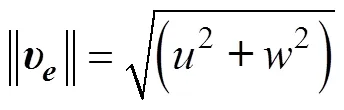
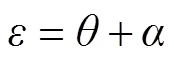
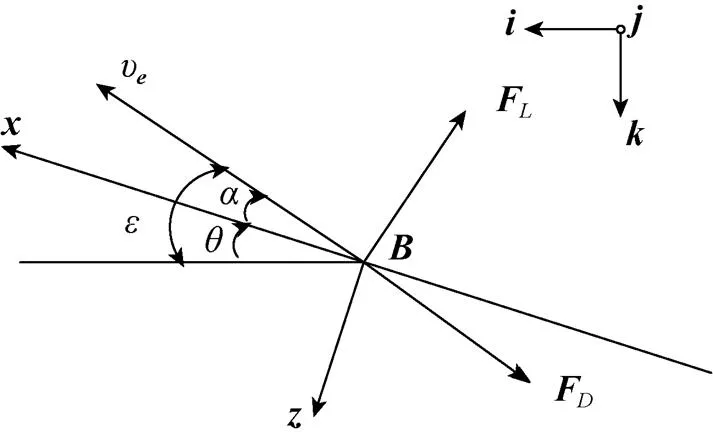
图4 锯齿形滑翔运动受力演示

机身所受阻力与运动方向相反, 升力垂直于阻力, 其大小与攻角的关系式为[16]

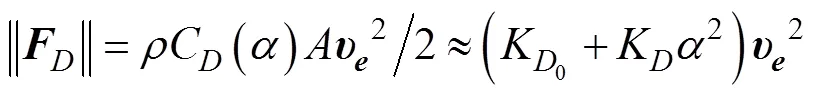
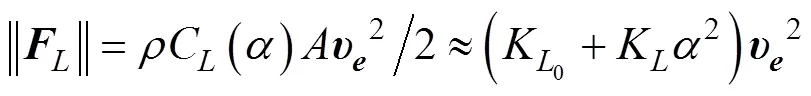
水下滑翔机回转性能与外形尺寸、航行速度、尾舵升力和整体阻力相关, 见图5。尾舵面积是影响舵力的重要参数, 一般采用挪威船级社(det norske veritas, DNV)范式计算公式进行估算[8]

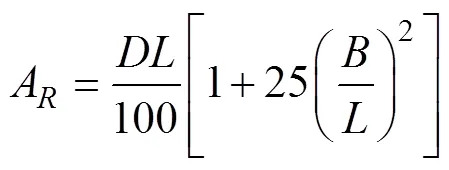
图5 Petrel-II 200外形尺寸

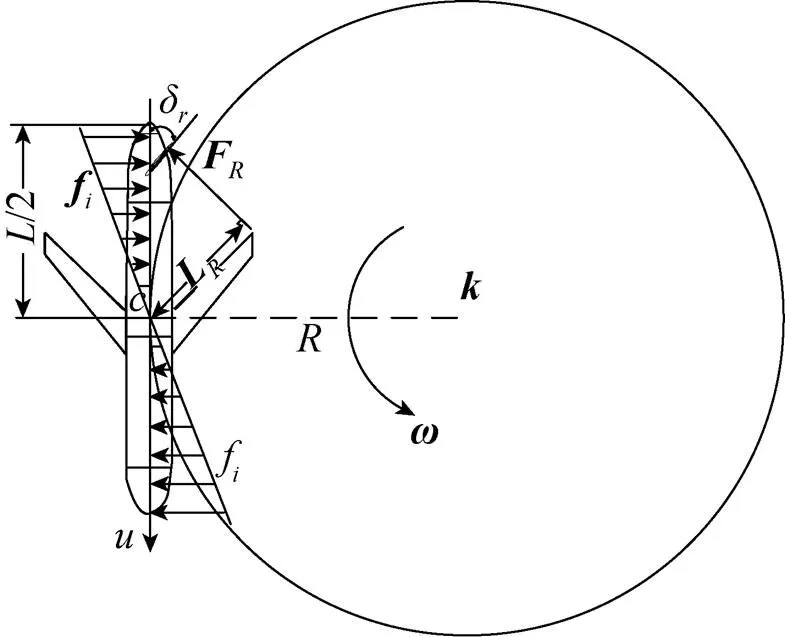
图6 Petrel-II 200回转受力图

假设来流与航速之间的夹角为0, 利用藤井公式计算舵力与转向力矩为

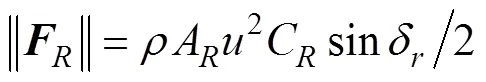
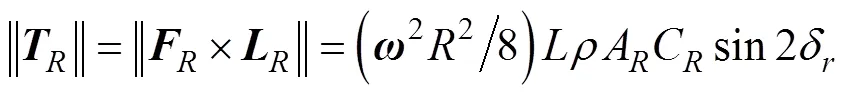
由于机体是规则回转体, 定轴转动所受水阻力及水阻力矩为

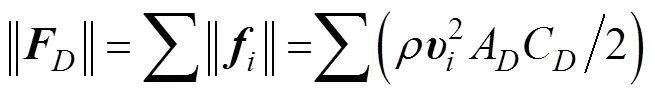
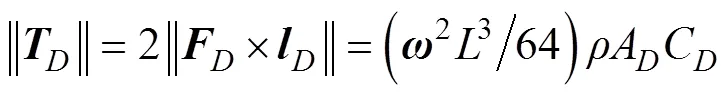
当水下滑翔机处于稳定回转状态时, 在地系中绕轴回转, 水阻力矩与回转力矩平衡, 联立式(27)~(31)可得水下滑翔机的回转半径表达式

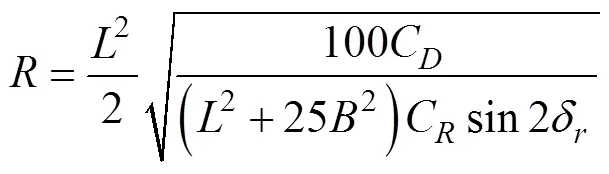
3 Petrel-II 200运动仿真

3.1 参数赋值

水下滑翔机在工作过程中大部分时间处于稳态运动, 除了固定的几何参数不变外, 机体的转动惯量净排水量等物理参数也几乎不变, 在运动仿真中可看作常量, 见表2。

表2 Petrel-II 200几何物理参数

利用计算流体动力学(computational fluid dynamics, CFD)软件计算得出Petrel-II 200在稳态运动下的水动力系数, 附加质量的计算方法参考文献[15], 见表3。

锯齿形剖面与螺旋回转运动是Petrel-II 200的主要运动方式, 几乎囊括了内部调节模块所有的工作过程, 故对其进行针对性仿真研究。

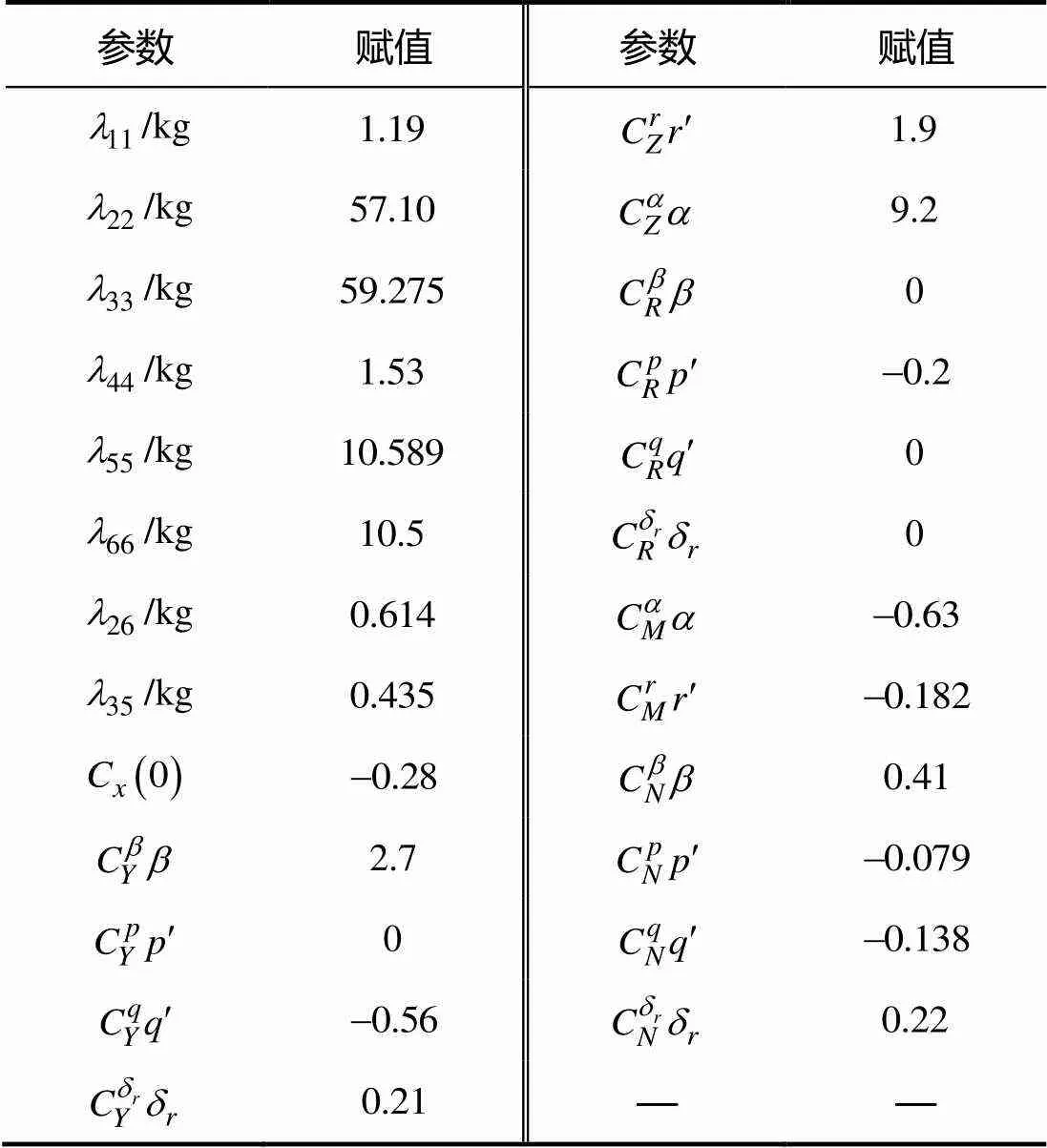
表3 Petrel-II 200水动力系数及附加质量

表4列出了2种运动模式的控制变量变化范围, Petrel-II 200将以此作为输入, 通过Matlab软件应用Runge-Kutta法[9]进行迭代计算, 输出运动轨迹、运动参数与迭代次数之间的变化曲线。

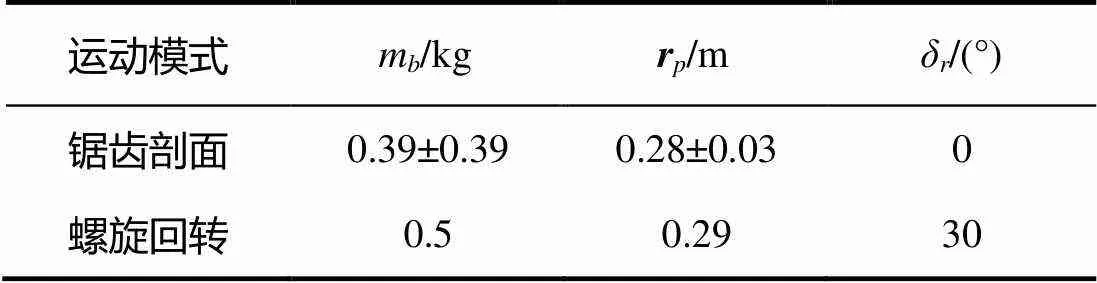
表4 2种运动模式控制参数变化范围

3.2 仿真结果

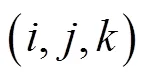
Petrel-II 200通过浮力及俯仰调节模块的周期性变化, 借助水对机翼的作用力进行斜上及斜下滑翔。从图中可看出Petrel-II 200的仿真轨迹呈锯齿形, 在地系下的纵向位移均匀增加, 使得纵向速度保持恒定, 竖向位移的周期变化使得俯仰角、攻角和竖向速度也周期性的改变方向; 另外, 在拐点处俯仰角出现震荡现象, 对应的速度与角速度也发生局部骤变, 这是由于浮力与俯仰调节模块因调节速率不同产生的耦合作用现象, 一段时间后将恢复稳定。

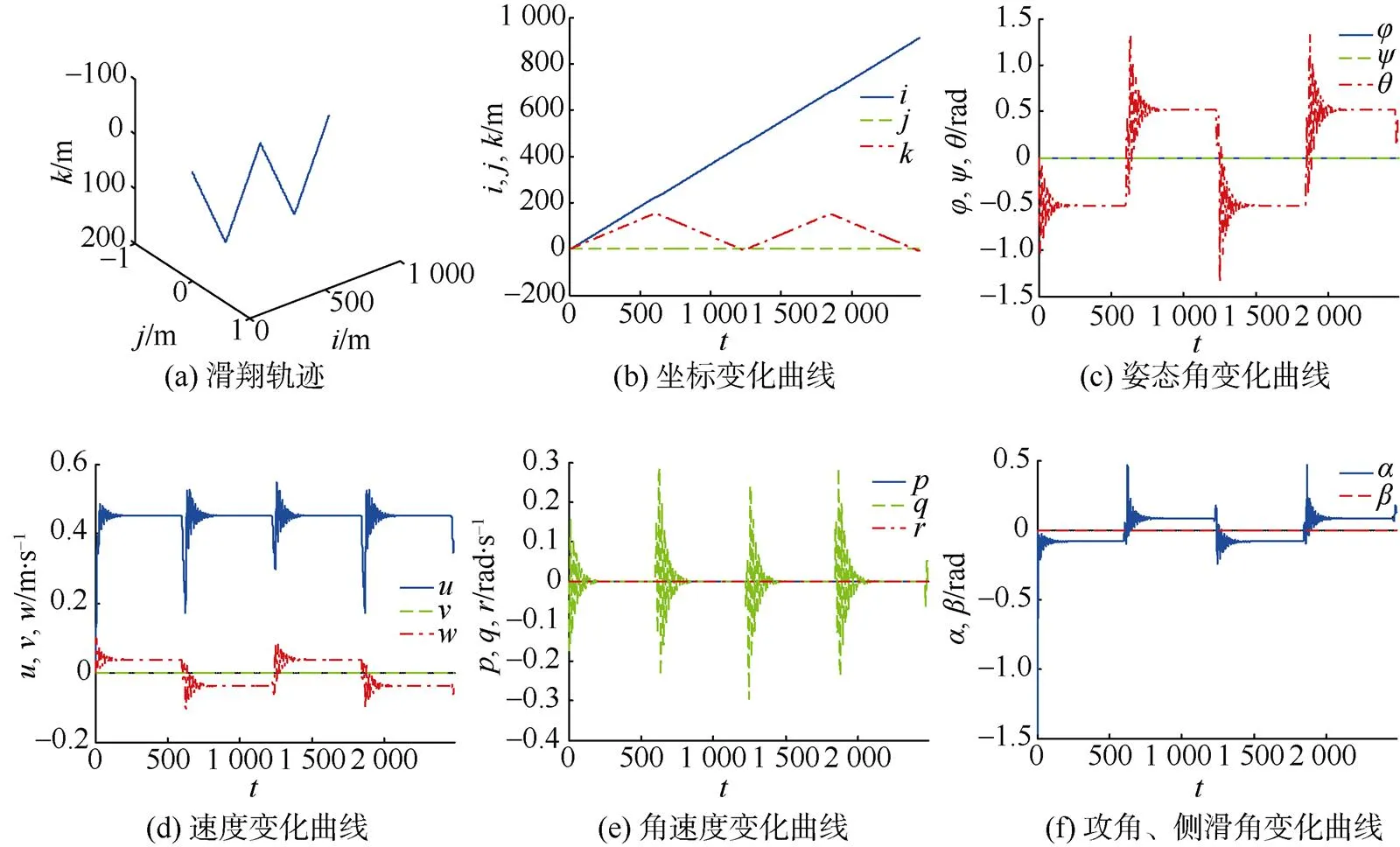
图7 锯齿形剖面运动仿真曲线

从图8中可看出, 转舵30°后, Petrel-II 200在俯仰与浮力模块调节至合适的位置前会因耦合作用产生震动, 速度与角度会受一定影响。待运动状态稳定后, 滑翔轨迹呈匀速螺旋回转下降,横纵位移、速度、角速度、攻角及俯仰角均保持恒定, 只有偏航角周期性变化、下潜深度均匀增加。

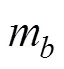
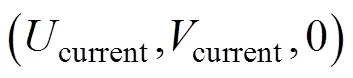
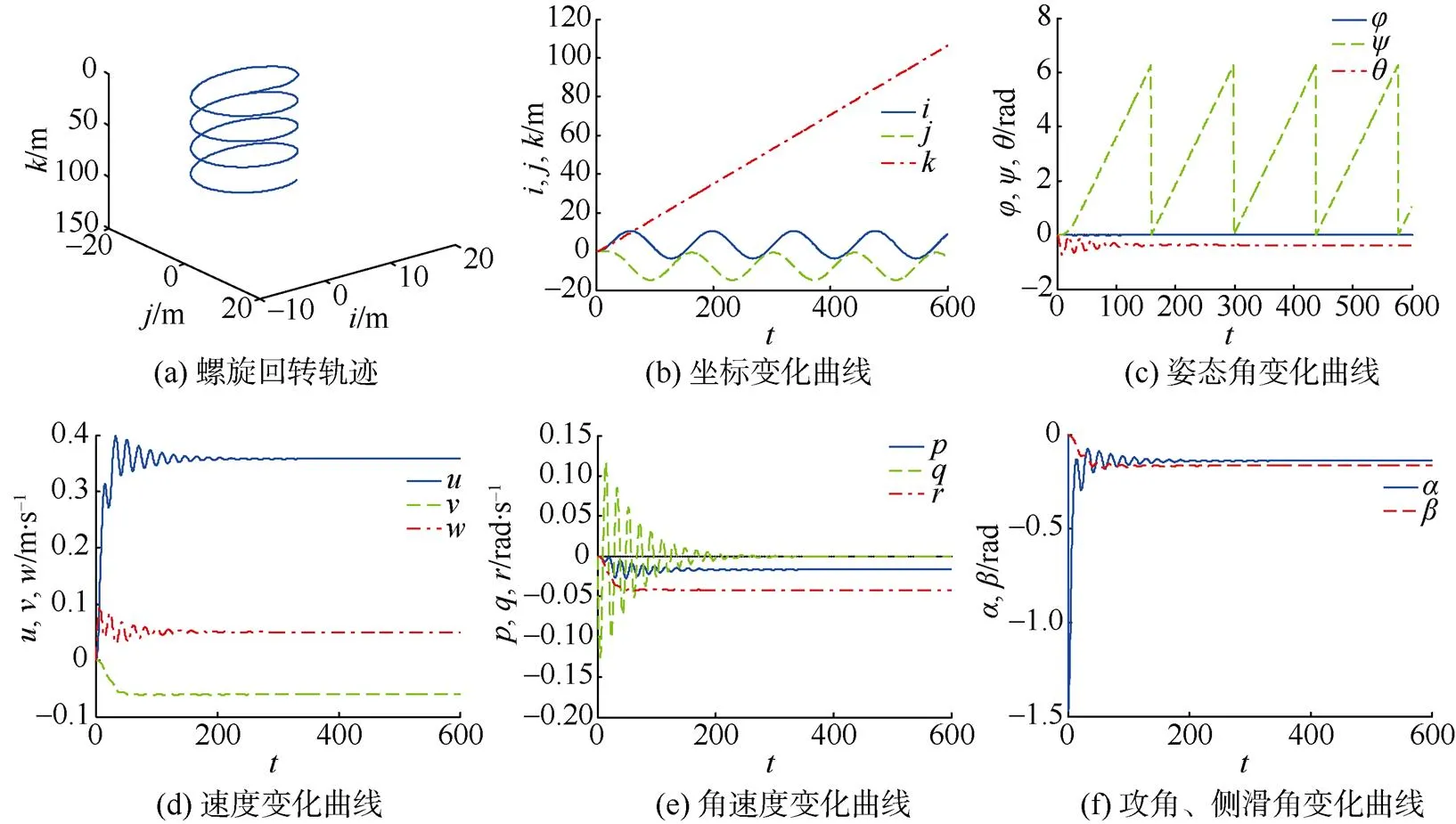
图8 螺旋回转运动仿真曲线

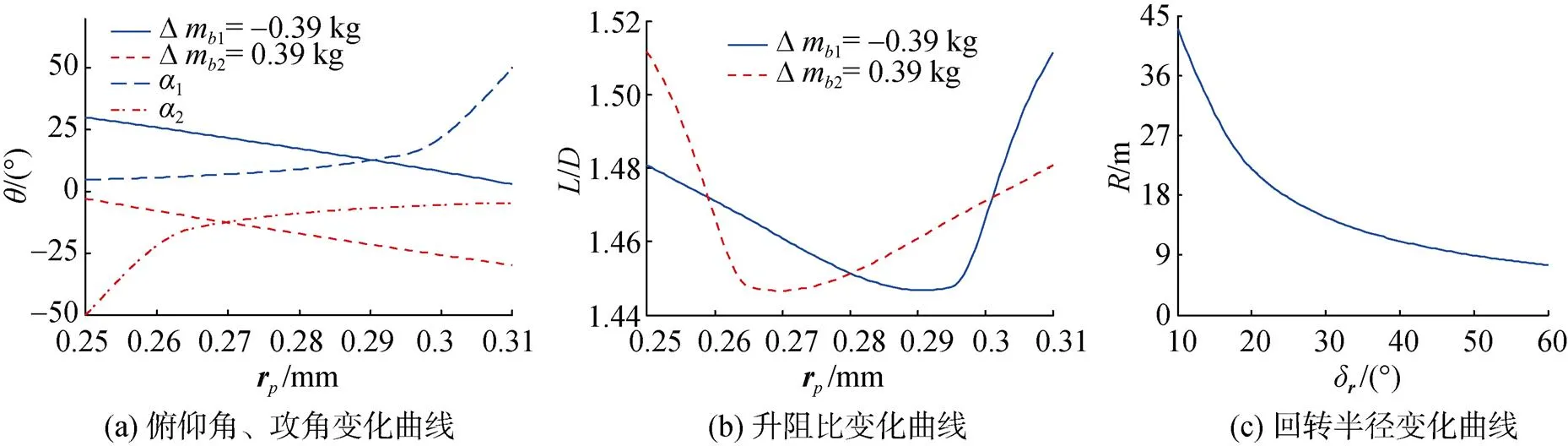
图9 俯仰角、攻角与升阻比随控制变量变化曲线

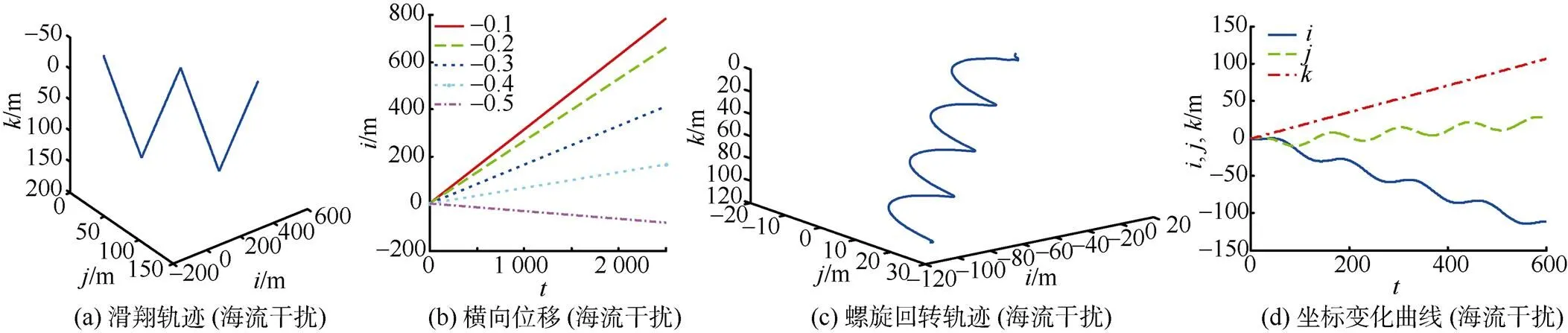
图10 海流干扰下的运动轨迹

4 结束语

文中采用动力学理论对浅海型、尾舵转向的Petrel-II 200进行动力学建模, 推导出动力学方程, 初步探索了控制变量与水下滑翔机位姿及回转性能之间的关系, 并对有代表性的特殊运动进行了运动仿真, 其仿真所得滑行轨迹和运动参数变化与理想和海流干扰下的运动模式相符, 验证了动力学方程推导的正确性, 为该平台的运动机理解析、运动性能提升和控制算法设计给出了理论依据。目前, 海流对Petr- el-II 200的运动性能还有很大的影响, 下一步将探讨如何抵消海流对水下滑翔机产生的干扰, 优化平台的运动性能。

[1] Rudnick D L, Davis R E, Eriksen C C, et al. Underwater Gliders for Ocean Research[J]. Marine Technology Soci- ety Journal, 2004, 38(2): 73-84.

[2] Leonard N E. Control Synthesis and Adaptation for an Underactuated Autonomous Underwater vehicle[J]. IEEE Journal of Oceanic Engineering, 1994, 20(3): 211-220.

[3] Leonard N E. Periodic Forcing, Dynamics and Control of Underactuated Spacecraft and Underwater Vehicles[C]// Decision and Control, 1995. New Orleans, LA, USA: IEEE, 1996: 3980-3985.

[4] 俞建成, 张奇峰, 吴利红, 等. 水下滑翔机器人运动调节机构设计与运动性能分析[J]. 机器人, 2005, 27(5): 390-395.

Yu Jian-cheng, Zhang Qi-feng, Wu Li-hong, et al. Movement Mechanism Design and Motion Performance Analysis of an Underwater Glider[J]. Robot, 2005, 27(5): 390-395.

[5] 王长涛, 俞建成, 吴利红, 等. 水下滑翔机器人运动机理仿真与实验[J]. 海洋工程, 2007, 25(1): 64-69.Wang Chang-tao, Yu Jian-cheng, Wu Li-hong, et al. Reseach on Movement Mechanism Simulation and Experiment of Underwater glider[J]. Ocean Engineering, 2007, 25(1): 64-69.

[6] Zhang S, Yu J, Zhang A, et al. Spiraling Motion of Underwater Gliders: Modeling, Analysis, and Experimental Results[J]. Ocean Engineering, 2013, 60(3): 1-13.

[7] 王树新, 刘方, 邵帅, 等. 混合驱动水下滑翔机动力学建模与海试研究[J]. 机械工程学报, 2014, 50(2): 19-27.Wang Shu-xin, Liu Fang, Shao Shuai, et al. Dynamic Modeling of Hybrid Underwater Glider Based on the Theory of Differential Geometry and Sea Trails[J]. Journal of Mechanical Engineering, 2014, 50(2): 19-27.

[8] 武建国. 混合驱动水下滑翔机系统设计与性能分析[D]. 天津: 天津大学, 2010.

[9] 孙秀军. 混合驱动水下滑翔机动力学建模及运动控制研究[D]. 天津: 天津大学, 2011.

[10] Wang S X, Sun X J, Wu J G, et al. Motion Characteristic Analysis of a Hybrid-driven Underwater Glider[C]//Oce- ans. Sydney, NSW, Australia: IEEE, 2010: 1-9.

[11] Wang S X, Sun X J, Wang Y H, et al. Dynamic Modeling and Motion Aimulation for a Winged Hybriddriven Underwater Glider[J]. China Ocean Engineering, 2011, 25(1): 97-112.

[12] Niu W D, Wang S X, Wang Y H, et al. Stability Analysis of Hybrid-driven Underwater Glider[J]. China Ocean En- gineering, 2017, 31(5): 528-538.

[13] 王延辉. 水下滑翔机动力学行为与鲁棒控制策略研究[D]. 天津: 天津大学, 2007.

[14] 温浩然, 魏纳新, 刘飞. 水下滑翔机的研究现状与面临的挑战[J]. 船舶工程, 2015(1): 1-6.Wen Hao-ran, Wei Na-xin, Liu Fei. Research of Current Situation and Future Challenges of Underwater Glider[J]. Ship Engineering, 2015(1): 1-6.

[15] 李天森. 鱼雷操纵性[M]. 第2版. 北京: 国防工业出版社, 2007.

[16] Graver J G. Underwater Gliders: Dynamics, Control and Design[D]. Princeton: Princeton University, 2005.

Dynamic Modeling and Simulation of Underwater Glider Petrel-II 200

SUN Xiu-jun1,2,3, WANG Lei1, SANG Hong-qiang4

（1. School of Mechanical Engineering, Hebei University of Technology, Tianjin 300130, China; 2. Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China; 3. Laboratory of Marine Dynamics and Climate Function, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China; 4. School of Mechanical Engineering, Tianjin Polytechnic University, Tianjin 300387, China）

In China, the researches on dynamic behavior of underwater glider mostly focuses on deep-sea type and horizontally rolling mechanism, but less on shallow-sea type and tail rudder steering type. This paper takes shallow-sea underwater glider Petrel-II 200 as a model to conduct dynamic modeling and motion simulation, and adds some disturbing factors such as ocean current for the purpose of providing reference for motion form of shallow-sea underwater glider. According to the relative motion relationship of each mass in the Petrel-II 200 three-dimensional model, the centroid is simplified to a multi-rigid body system composed of multiple particles, and the relationship between the centroid and the particle is constructed. Based on the theorems of momentum and momentum moment, the dynamics of Petrel-II 200 is analyzed. The gravity, driving buoyancy and hydrodynamics of the underwater glider are transformed into body coordinate system. The complete dynamic equation is deduced, and the expressions of lift-to-drag ratio and radius of rotation are defined. By choosing the physical and hydrodynamic parameters of the underwater glider, simulation experiments of typical motions, such as sawtooth and spiral motions, are carried out. The simulation results validate the accuracy and reliability of the dynamic model, and provide a good simulation platform for the following underwater glider Petrel-II 200 motion performance optimization and control algorithm design.

underwater glider; dynamic model; kinetic equation; motion simulation

TJ630; U674.941; O352

A

2096-3920(2019)05-0480-08

10.11993/j.issn.2096-3920.2019.05.002

孙秀军, 王雷, 桑宏强. Petrel-II 200水下滑翔机动力学建模及仿真[J]. 水下无人系统学报, 2019, 27(5): 480-487.

2018-10-25;

2018-12-10.

国家重点研发计划重点专项(2017YFC0305902); 青岛海洋科学与技术国家实验室“问海计划：项目(2017WHZ ZB0101); 天津市自然科学基金重点基金(18JCZDJC40100).

孙秀军(1981-), 男, 教授, 主要研究方向为海洋移动观测平台技术.

(责任编辑: 杨力军)