一种异型改进的自适应遗传算法

冯九林，殷 锋，黄光华

(西南民族大学计算机科学与技术学院，四川 成都 610041)

遗传算法(Genetic Algorithm， 简称GA)[1-2]是一种经典的全局优化算法，其交叉概率和遗传概率值的数据类型是一种静态浮点型，一般采用穷举法试探出一个能使搜索效果达到最好的定值，取一定值显然对整个搜索过程是欠佳的.因此有了自适应遗传算法(Adaptive GA，简称AGA)[3-4]的诞生，AGA 采用线性数学公式来自适应调整遗传算子的交叉概率和变异概率值，自适应调整改进后，GA 的收敛速度[5]虽有所提高，但是AGA 在演化过程中仍然存在明显的早熟现象.

文章提出了的HIAGA，让交叉算子中的交叉概率值和和变异算子中的变异概率值随着文中提出的曲线变化而变化，通过对个体的适应度、每次进化的种群的平均适应度以及每次进化的种群中的最大适应度的相机组合得到一个值，该值[9]常用以衡量个体适应度变化，故文中称该值为个体适应度变化率，用符号∂表示(如公式4 所示).种群中个体适应度和∂成正比例关系，而∂的改变使交叉概率值和变异概率值呈曲线变化.不同适应度的个体通过文章中所提出的曲线能自适应分配到一个利于进化的概率值，从而使劣质个体快速进化成优质个体，使优质个体和进化过程没有停滞的机率.再结合精英保留策略思想，减小优质个体的破坏率，进一步提升收敛速度和精确度.

1 线性自适应遗传算法

在标准自适遗传算法AGA 中，线性自适应[6-8]调整遗传算子的交叉率和变异率的公式可详见文献[7]，公式中会存在Pc 或Pm 为零时的状况，而出现这种状况时，整个进化过程几乎只有选择算子在作用，破坏了该算法进化理论的核心思想，若此时的优良个体并不是全局最优解，则得到的最终结果极可能会是局部极值[9-11]，从而失去了该算法建立的意义.因此文献[9]在此基础上提出了一种改进的线性AGA( LinearAdaptive GA，以下简称LAGA)[12-14]，使群体中最大适应度的个体不会因为其交叉率和变异率为零而使进化过程停滞.其调整公式[15]如公式(1)及公式(2)所示，该调整公式的详细信息及应用见文献[15].

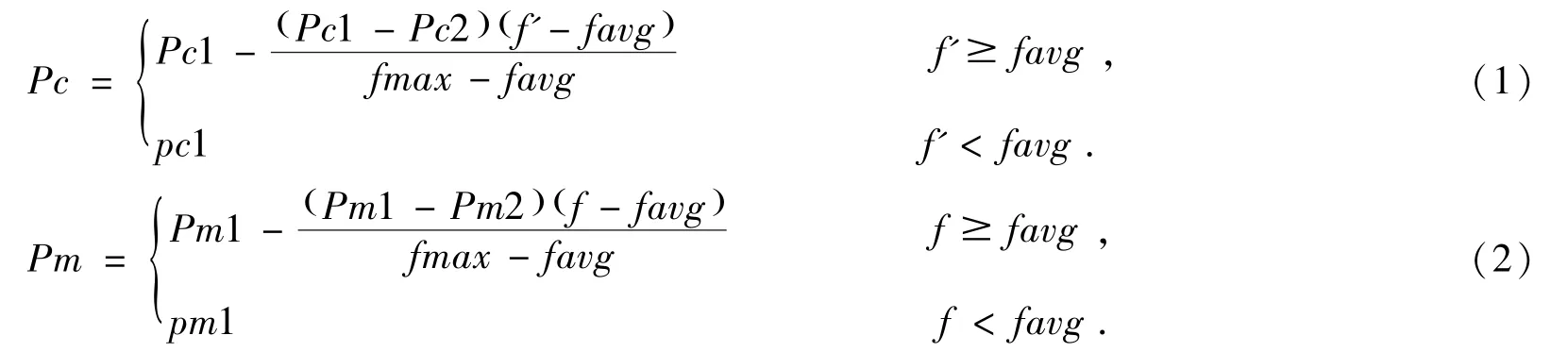
在LAGA 中，虽然有效的弥补了AGA 中的不足，但却忽视了改进后的不足之处.在上述公式中，当种群中favg 趋近于fmax 时，公式中分母趋近于零，导致整个分式趋向于无穷小，使得Pc 和Pm 趋向于无穷小.从而也会有交叉算子和变异算子失效，仅选择算子有效的现象发生.

2 改进的自适应遗传算法

2.1 交叉概率Pc 值和变异概率Pm 值的曲线调整

通过了解文献[7]的曲线调整分析，本文在数学领域中得到一种曲线函数，由双曲正弦和双曲余弦这两种基本双曲函数推导而来的Tanh 函数，即双曲正切函数，通过对双曲正切函数求导得到其导数公式后得到公式(3)，当x=0 时，f(x) = 1；通过计算得出，当x ≥5.512 时，f(x) 无限趋近于零，且该函数在整个定义域中的值域属于(0 -1].

从公式(4)可以看出，当f ≥favg 时，个体适应率∂与个体适应度f 成正比.当个体适应度f =fmax 时，∂=1.在求解最大优化问题时，可利用公式(5)调整算法中的交叉概率值，而公式(6)则可用以调整算法进化过程中的变异概率.此式中，β =5.512，Pcmax 和Pcmin 分别为交叉率的上界和下界；Pmmax 和Pmmin 分别为变异率的上界和下界.

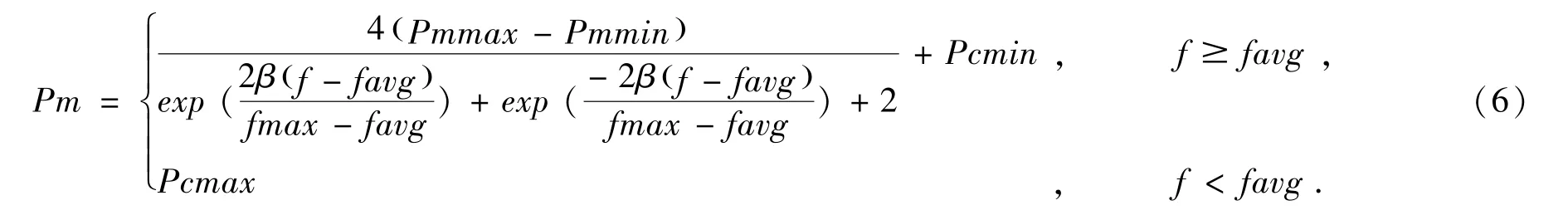
公式(5)的几何图形如图1 中(a)所示，其形如高斯分布曲线，Pcmax 和Pcmin 分别代表最大交叉概率和最小交叉概率，Pc 和∂分别为交叉概率和个体适应度变化率；∂min 和∂max 分别为求函数最大值时的最小个体适应率和最大个体适应率；而∂'min、∂'及∂'max 分别是求函数最小值时的最小个体适应率、个体适应度变化率和最大个体适应率.结合公式(5)从图1 中(a)可以分析出，随着个体适应度增大到与种群中最大个体适应度接近或者相等时，则∂无限接近乃至等于∂max，此时对应的则是最小交叉概率Pcmin；当种群中个体适应度很小时，则∂接近甚至相等∂min，此时对应的则是最大交叉概率Pcmax.同理，在求函数最小值问题的时候对应坐标轴负半轴的部分，∂avg 表示种群中个体适应度达到平均适应度时，种群中个体的个体适应率的值.公式(6)的几何图形如图1 中(b)所示，Pmmax 和Pmmin 分别表示最大变异概率和最小变异概率，Pm 和∂c 则分别代表变异概率和个体适应度变化率；∂cmin、和∂cmax 分别为求函数最大值时的最小个体适应率以及最大个体适应率；而∂'cmin、∂'及∂'cmax 分别是求函数最小值时的最小个体适应率、个体适应率和最大个体适应率.

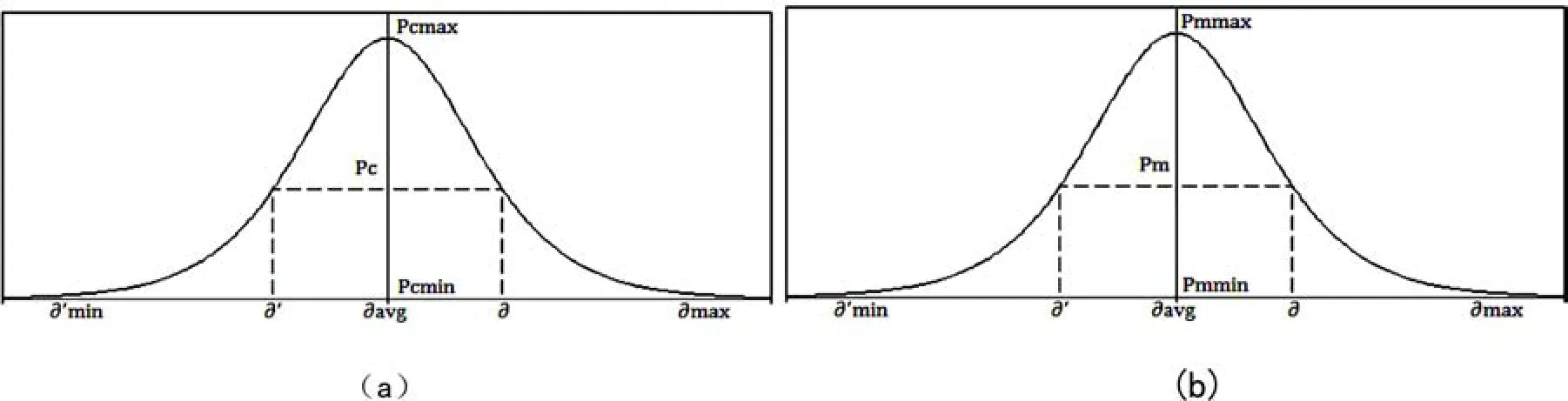
图1 HIAGA 交叉概率(a）和变异概率(b）自适应调整曲线Fig.1 Crossover probability(a） and mutation probability(b） for adaptive adjustment curve of HIAGA

结合公式(6)从图1 中的(b)可以分析出，随着个体适应度增大到与种群中最大个体适应度无限接近或者相等时，则∂无限接近或等于∂max，此时变异概率Pm 对应的则是最小变异概率Pmmin；当种群中个体适应度很小时，则∂无限接近甚至等于∂min，此时pm 对应的则是最大变异概率Pmmax.

遗传算法线性自适应调整的不足之一就是自适应调整的变化率太大，不能很好的把握算法初期和后期自适应调整的‘度’，则导致了算法在函数全局寻优的过程中陷入局部最优解.而在HIAGA 中，进化过程的初期和后期正好弥补了AGA 和LAGA 算法的不足，在初期和后期，利用该函数曲线的特性，小量的调整交叉率和变化率，使自适应更加合理.且利用该函数的对称性，在求函数最小值时，该曲线自适应调整公式不用有太大的改动，只需将fmax 改为fmin.当求解函数最小值时，适应度是负值，此时β = -5.512，且对应的函数图像是图1中函数图像负半轴部分.

2.2 精英保留策略

精英保留策略的方法是在种群进行遗传操作之前将种群中适应度最大的个体挑选出来，以防止种群中最优的个体在交叉算子和变异算子操作中丢失.在本文改进的算法中，借鉴了精英保留策略的思想，通过上文中个体适应率∂来判断该个体是否是适应度最大的个体，当∂=1 时，该个体是适应度最大的个体，则复制该个体后再进行变异算子操作，再将操作后的子代插入到新种群中.本文算法中的精英保留策略加入变异算子是因为当个体适应度很大时，变异算子的变异率值随非线性调整曲线缓慢变化，优质个体被破坏的几率很小，且让个体适应度大的而非全局最优解的个体快速进化到全局最优解. 本文改进的算法的执行流程如图2 所示，其中gen 是整型变量，∂是上文所提及的个体适应率.

图2 改进的算法的执行流程Fig.2 Execution flow of improved algorithm

3 仿真验证与性能分析

为了验证该改进算法的性能及有效性，选择一个具有代表性且相当复杂的函数(7)进行寻优测试.分别对普通的遗传算法(GA)，线性自适应遗传算法(LAGA)和文章提出的曲线自适应遗传算法(HIAGA)的全局最优解的寻找过程进行比较.

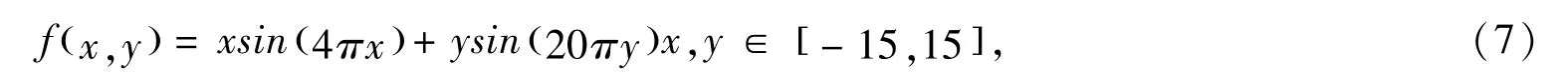
以该函数为目标函数，选择二进制编码[9]，采用常用的轮盘赌抽样选择方法.在HIAGA 中采用公式(5)、(6)进行自适应调整，公式中的参数Pc1 =0.8，Pc2 =0.6，Pm1 =0.04，Pm2 =0.006；在LAGA 中采用公式(1)、(2)进行自适应调整，初始化公式中的参数Pc1 =0.9，Pc2 =0.6， Pm1 =0.1，Pm2 =0.01；GA 调整公式参数为Pc =0.9，Pm=0.05，仿真结果如图3 -5 所示.

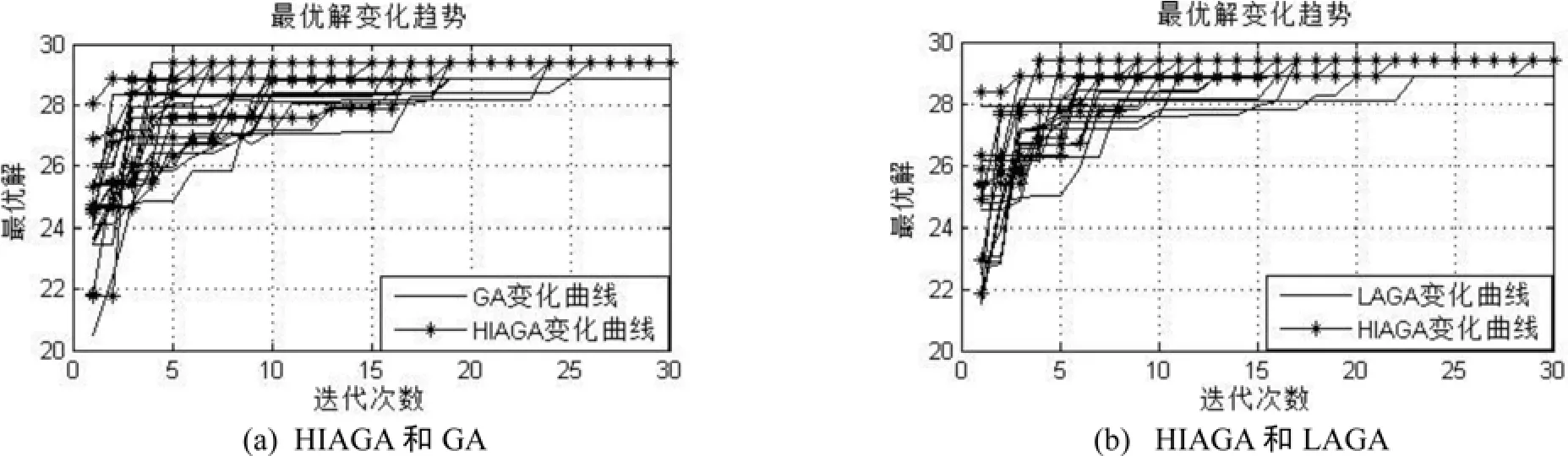
图3 30 次迭代最优解的变化Fig.3 The change of the optimal solution of 30 iterations

图4 70 次迭代最优解的变化Fig.4 The change of the optimal solution of 70 iterations

图5 150 次迭代最优解的变化Fig.5 The change of the optimal solution of 150 iterations

上述图中，带“∗”的实线均代表HIAGA，实线表示GA 和LAGA.图3 是算法经过30 次遗传迭代后，得到的比较结果，图3 中的(a)和(b)均是运行10 次后得到的结果，可以看出GA 和LAGA 偶尔有出现早熟现象而收敛到了局部最优解，而HIAGA 收敛速度较快且未出现早熟现象；图4 是算法经过70 次遗传迭代后，得到的比较结果，图4中的(a)和(b)中均运行10 次后可以看出GA 和LAGA 仍然偶尔有出现早熟现象，而HIAGA 收敛速度较快且未出现早熟现象；图5 是算法经过150 次遗传迭代后得到的比较结果，图5 中的(a)和(b)中亦均运行10 次，HIAGA 的收敛速度比GA 和LAGA 的收敛速度都较快且曲线呈现较好的阶梯状，具有优良的自适应能力.

4 结语

相比与其它智能算法，遗传算法的发展历史较为悠久，但是就该算法的收敛速度和早熟现象仍然是研究人员不断探索和改进的领域.而针对这两个方面的问题，文章根据GA 和AGA 的相关理论和知识，对AGA 做出了相关改进.由MATLAB 软件实验仿真，得到的结果可知：文章中的HIAGA 对交叉算子中的交叉概率和变异算子的变异概率进行了自适应生成策略方面的改进，对算法收敛速度和避免算法早熟等问题上都能取得较好的效果.