我国沿海城市海洋经济效率的测度及其影响因素分析
——基于两阶段双重自助抽样DEA方法
朱新颜, 刘 健,刘 伟
(1.青岛农业大学 经济学院,山东 青岛 266109;2.中国海洋大学 文学与新闻传播学院,山东 青岛 266100)
引 言
海洋的开发与利用对于缓解我国资源紧张的矛盾,实现可持续发展战略具有重要作用。“十二五”以来,在世界经济持续低迷和国内经济增速放缓的大环境下,中国海洋经济在国家发展战略中的地位稳步提升,保持了平稳增长的态势。全国海洋生产总值平均增速7.5%,高于同期国民经济增长速度,海洋生产总值占GDP比重保持在9.3%以上。2015年10月,党的十八届五中全会通过《中共中央关于制定国民经济和社会发展第十三个五年规划的建议》,提出“拓展蓝色经济空间。坚持海陆统筹,壮大海洋经济”的指示。同时,在《国民经济和社会发展第十三个五年规划纲要》中,也规定实施陆源污染达标排海和排污总量控制制度,建立海洋资源环境承载力预警机制。这使得我国海洋经济未来发展总体向好的同时,也面临着一定程度的挑战。在这种海洋经济的快速发展与日益严峻的环境约束的背景下,海洋经济效率问题应当得到更大程度的重视,以提高海洋资源利用的综合效益。作为海洋经济的“排头兵”,我国沿海城市海洋经济的创新能力与竞争能力更强,发展也更为快速,研究其海洋经济效率问题,有助于指导和促进我国海洋经济又好又快地发展。
虽然专家学者对海洋在社会经济发展上所具有的重要性已达成共识,但在对海洋经济的定量化研究因而在海洋经济发展的对策建议上还存在着较大的分歧,这一状况的出现既与海洋经济、海洋部门在定义与统计表征上的多样性有关,也与数据的有限可得性和质量有关[1]。而且,国际上有关海洋经济的研究多集中于对海洋经济发展的评价指标的构建上[2]以及海洋经济对一国国家层面或区域层面的经济影响上[3],而对海洋经济效率问题的研究相对较少。近年来这一问题虽然引起了国内学者的关注,但相关研究亦较为有限。丁黎黎等(2018)测算了中国沿海11地区的海洋经济增长的生产效率、环境治理效率和综合效率[4]。吴淑娟等(2015)对我国蓝色经济区的海洋经济运行效率进行了测算以找出其中非效率环节[5]。赵昕等(2012)运用GRA-DEA混合模型对我国沿海地区海洋经济效率进行分析与评价[6]。杜军等(2016)采用数据包络分析法以及Malmquist生产率指数模型对我国沿海11个省份海洋经济效率进行评价[7]。由于基于传统方法的海洋经济效率测算未考虑资源环境约束与非期望产出,苑清敏等(2016)、赵林等(2016) 将资源投入与非期望产出同时纳入模型之中,对资源环境约束下的中国海洋经济效率进行评价并对其变化进行分析[8-9]。上述研究主要从我国省级层面展开,而由于数据的可得性,从市级层面进行的海洋经济效率的研究更为少见。目前可查阅到的一篇文献为范斐等(2011)对环渤海经济圈的17个沿海城市的海洋经济效率的评价分析[10]。而对我国沿海城市海洋经济效率的测算及其影响因素分析的文献尚未见到。
本文首次将基于双重自助抽样方法的DEA模型引入沿海城市海洋经济效率的研究中,一方面解决了小样本在传统效率评价方法中存在的效率值易被高估且缺乏统计推断的问题,另一方面在对影响海洋经济效率的因素进行统计推断时结果也更为可信。通过将影响海洋经济效率的环境变量进行分析,有助于明确促进以及制约沿海城市海洋经济效率提高的因素,这对提升沿海城市海洋经济效率、推动海洋经济高质量发展具有重要的意义。
1 研究方法
1.1 效率的测算方法
本文所指的效率为Farrell(1957) 提出的剔除了规模报酬影响后的技术效率[11],具体而言,是指在相同的产出下生产者理想的最小可能性投入与实际投入的比率,衡量的是生产者投入转化为产出的能力。测度技术效率的最为常见的方法为随机前沿分析法(Stochastic Frontier Analysis,SFA) 和数据包络分析法(DataEnvelopmentAnalysis,DEA)。SFA 是一种参数方法,通过设定生产函数确定生产前沿面进行技术效率的测算。这一方法由于设定了确定的随机前沿生产函数而可以将随机误差项纳入模型之中,因而考虑了随机因素对生产前沿面的影响,这是相较于DEA方法所具有的主要优势。而缺点在于生产函数形式的设定与随机误差项的分布假设会直接影响效率的测算结果。DEA是一种非参数方法,其通过线性规划技术确定生产前沿面进行每个决策单元(decisionmakingunit,DMU) 的相对效率的测算,其优点是无须设定具体的生产函数与预先估计参数,且无须考虑投入产出数据量纲的同一化,因而在避免主观因素影响、简化算法与减少误差等方面有着巨大的优越性,因而成为管理科学领域重要和有效的分析工具。这一方法的主要缺点在于无法测度随机误差项的影响。对本研究而言,研究目标主要在于确定影响我国沿海城市海洋经济效率的因素,因而采用无须设定生产函数的DEA方法即可达到目标,并可避免由于生产函数的错误设定而带来的效率测算结果上的偏误。
1.2 传统两阶段DEA方法及其缺陷
传统的两阶段法,由Ray(1991) 首次提出[12],其步骤为:在第一阶段,运用传统的DEA方法来求得决策单元的效率值;在第二阶段,将第一阶段求解的效率值作为被解释变量,以环境变量作为解释变量进行回归分析,从而得出环境变量对效率的影响方向。由于效率值(被解释变量) 介于0和1之间,故在后来改进的研究中,研究者在第二阶段中用Tobit模型代替了普通的回归模型[13-14]。
传统两阶段法的主要缺点在于:首先,在第一阶段中,由于传统的DEA方法未能就效率值进行统计推断,未考虑效率估计量的不确定性,因而常常会出现效率值被高估的情况,进而可能将本来无效的决策单元判定为有效,这使得DEA效率值的可靠性大为降低[15];其次,第二阶段的回归分析违背了回归分析基本假设中的独立性假设:一方面,由于传统的DEA方法中对每个DMU效率值的计算都要涉及样本中所有的DMU,故在第二阶段中作为被解释变量的DEA效率值之间并不独立,从而违背了回归分析中样本间相互独立的基本假设;另一方面,第一阶段中计算DEA效率值所使用的投入、产出变量通常与第二阶段作为解释变量的环境变量相关,因而违背了回归分析中误差项与自变量相互独立的假设[15]再次,Simar等 (2007)、Banker等 (2008) 研究发现,传统的两阶段DEA方法中第二阶段为研究者通常采用的Tobit回归模型的估计结果是有偏和不一致的[16-17]。这是由于真实的效率值无从观察,而只能以第一阶段中得出的DEA生产效率估计值来代替,而这更加符合截断数据的特点,故Tobit回归模型并不适合。
1.3 两阶段双重自助抽样DEA方法
针对传统两阶段DEA方法所具有的缺陷,Simar等(1998) 首次将Bootstrap方法运用到DEA效率值的估计中,即通过对来自未知总体分布的原始小样本观测数据进行有放回的重复再抽样,从而得到大量的Bootstrap样本以及对应效率值的Bootstrap统计量,利用大量的Bootstrap样本来估计效率值的总体分布,进而给出置信区间和纠偏修正后的DEA效率值[15]。这一方法解决了传统DEA方法缺乏统计推断以及由于样本量过小所导致的测算的效率值容易高估的问题。在此基础上,进一步做出改进,考虑了环境因素对真实效率水平的影响,通过运用双重自助抽样(Double Bootstrap) 方法,得出加入环境因素影响的纠偏修正后的效率值,并解决了传统两阶段DEA方法中第二阶段回归分析违背独立性假设的问题。下面说明这一方法的具体实现。
Charnes 等 (1978) 在 Farrell(1957) 提出的单一投入与单一产出的技术效率概念的基础上,扩展为多投入多产出的DEA模型,即CCR模型[18]。然而,Farrell与CCR模型均假设规模报酬不变,之后Banker等(1984) 将规模报酬不变的限制取消,提出了规模报酬可变的BCC模型[19]。CCR模型与BCC模型成了学术界最有影响力的DEA模型[20]。
本文基于沿海城市海洋经济的发展特点,采用投入导向的BCC模型,基本形式如下:
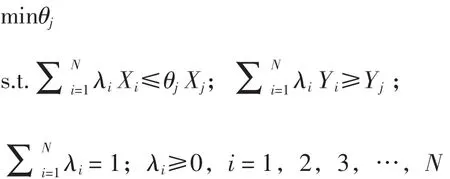
其中,样本S(=s1,s2,s3,…,sN)中包含了N 家 DMU,第j(=1,2,3,…,N) 家DMUsj的投入和产出向量分别为Xj和Yj,即sj=(Xj,Yj)。通过线性规划即可求得DMUsj在规模报酬可变条件下的初始效率值
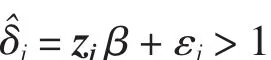
运用Bootstrap方法,重复以下步骤L1次,获得一组自助样本估计值
(1) 对每一个 DMUj(=1,2,3,…,N),从左侧截尾于的正态分布中随机抽取一个εj;
(2) 对每一个 DMUj(=1,2,3,…,N),计算
(3) 对每一个 DMUj(=1,2,3,…,N),令
(4) 替换第j(=1,2,3,…,N) 家DMUsj的投入和产出向量Xj和Yj为运用投入导向的BCC模型得出
至此,对每一个DMUj(=1,2,3,…,N),根据已计算的投入距离函数值δˆj以及自助样本估计值即可计算纠偏修正后的投
再次运用Bootstrap方法,重复以下步骤L2次,获得一组自助样本估计值
对每一个 DMUj(=1,2,3,…,N),从左侧截尾于的正态分布中随机抽取一个εj;
对每一个 DMUj(=1,2,3,…,N),计算
2 指标的选取、数据来源与海洋经济效率的测度
2.1 指标的选取、数据来源
考虑了数据的可得性,本文研究对象为我国12个主要沿海城市,由于我国海洋产业类型主要为滨海旅游业、海洋交通运输业和海洋渔业,这三个产业增加值占2014年全国主要海洋产业增加值的76.94%,因此,选取代表这三个产业的3个投入指标与1个产出指标来测度沿海城市的海洋经济效率。3个投入指标包括国内旅游人数、码头长度、海水养殖面积,1个产出指标为海洋生产总值。研究数据主要来自《中国海洋统计年鉴》(2015年)、《中国城市统计年鉴》(2015年)与Wind。表1为2014年各项投入产出指标的数据特征。

表1 2014年投入产出指标的描述性统计
2.2 沿海城市海洋经济效率的测度
运用基于Bootstrap的投入导向BCC模型,可以得到沿海城市海洋经济纠偏修正后的效率值(见表2第2列)与考虑了环境因素影响后的纠偏修正效率估计值(见表2第3列)。结果发现,经过Bootstrap纠偏修正后的效率值比传统BCC模型下测算的效率值(见表2第1列)低,且存在统计意义上的显著差异,这是由于Bootstrap方法考虑了前沿面的非效率因素。这表明传统DEA方法估计的效率值是严重有偏的。因此,运用Bootstrap方法测算的技术效率估计值能够更加客观地反映沿海城市海洋经济中投入转化产出的能力和真实效率水平。然而,上述效率测算并没有考虑环境因素对效率的影响,既然一个城市海洋经济的效率高低可能来自自身管理水平,也可能是来自环境因素的差异。研究发现,加入了环境影响因素后,沿海城市海洋经济效率值相较于未考虑环境因素的Bootstrap纠偏修正后的效率值有所提高,且具有统计意义上的显著差异,但同样低于传统BCC模型估计结果,这一差异也具有显著的统计学意义。

表2 沿海城市海洋经济效率估计结果
从沿海城市海洋经济效率排名来看,除个别城市外,不同模型下上述排名大致保持一致,其中烟台、汕头位居前列,而宁波、天津排名靠后。厦门、上海在传统BCC模型下效率排名第一,但针对这一传统DEA方法的缺陷加以修正后,发现其海洋经济效率排名最低,在考虑了环境因素的影响后,虽然效率排名有所提升,但仍位居中后位。这也验证了Simar等的论断:传统DEA方法可能将本来无效的DMU误判为有效[15]。另一个城市是海口,基于Bootstrap方法测算的DEA效率值显示其效率水平中等,然而,在考虑了环境因素后,其效率排名上升至第一位,与传统DEA方法下得出的结果一致。这表明环境因素而非其自身管理水平是造成海口海洋经济真实效率偏低的原因。
对考虑了环境因素影响后的沿海城市效率测算结果的进一步分析表明,12个沿海城市海洋经济效率均值为0.567,其中效率达到相对有效的城市有2个,占16.667%;大部分沿海城市海洋经济效率值处于无效区间,其中DEA无效程度高 (0≤m<0.5) 有 4个,占33.333%,DEA无效程度中等(0.5≤m<0.7)有5个,占41.667%,DEA无效程度低有1个,占8.333%,见表3。其中,海口、烟台、汕头处于DEA无效程度低与相对有效这两个层次,除海口外,烟台、汕头在基于Bootstrap方法测算的DEA效率排名中也位居前列,即使考虑了环境因素的影响,其排名也未见明显变化,表明这两个城市海洋经济效率较高。
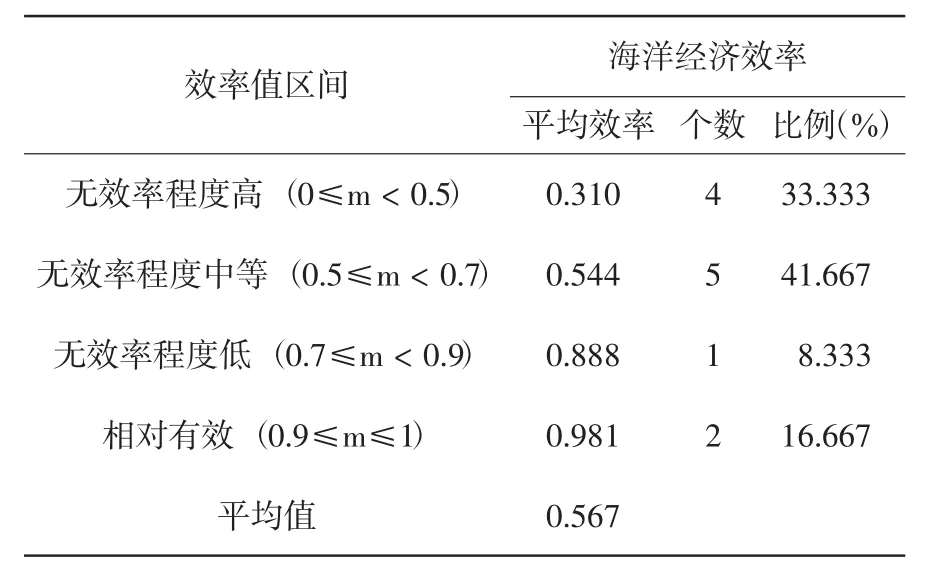
表3 沿海城市海洋经济效率估计结果分析
3 沿海城市海洋经济效率的影响因素实证分析
3.1 断尾回归模型设定
本文设定的断尾回归模型的形式为:
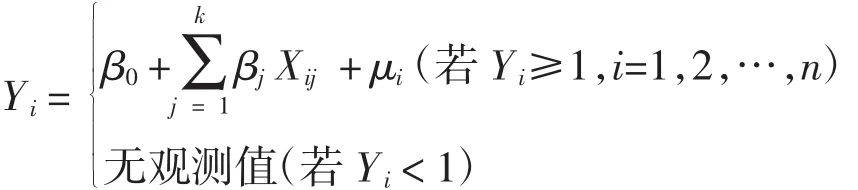
这一模型与Tobit回归模型的关键不同之处在于,当Yi<1时,没有任何有关 {Yi,Xi}的数据。模型中,Yi代表海洋经济无效率,以投入距离函数值表示,即各个沿海城市与有效前沿面的距离(亦即各DMU效率值的倒数),Xi表示各个影响沿海城市海洋经济效率的环境因素,βj为各个解释变量的回归系数,μ为随机误差项。对这一模型,可采用极大似然法进行估计,基于Bootstrap获得稳健系数估计值。
3.2 变量选取及描述性统计
在参考相关研究的基础上,本文选取人均GDP(X1)、海洋生产总值占城市生产总值的比重(X2)、进出口额占城市生产总值的比重(X3)、城镇固定资产投资额(X4)、工业污染防治投资当年施工项目数(X5)、废水排放量(X6)6个指标作为影响沿海城市海洋经济效率的因素,表征沿海城市经济发展水平、海洋经济发展水平、对外开放程度、环境保护力度与环境污染程度。而因变量为考虑了环境因素的纠偏修正后的效率值的倒数(Y1),即决策单元与生产前沿面之间的距离,其表示沿海城市海洋经济的无效率程度。
为与传统的两阶段DEA模型相比较,本文以传统BCC模型下测算的DEA效率值的倒数(Y2)为因变量,利用Tobit模型对影响海洋经济效率的因素进行回归分析。同时,本文也以考虑了环境因素的纠偏修正后的效率值的倒数(Y1)为因变量,利用Tobit模型对影响海洋经济效率的因素进行回归分析,以与前述断尾回归模型的估计结果进行对比。
影响海洋经济效率的因素的指标数据来自《中国海洋统计年鉴》(2015年)、《中国城市统计年鉴》(2015年) 与Wind。各变量的定义及描述性统计见表4。

表4 沿海城市海洋经济效率相关变量定义及其描述性统计
3.3 模型回归结果分析
以考虑了环境因素的纠偏修正后的效率值的倒数(Y1)为因变量,运用断尾回归模型对影响被解释变量的各因素的系数进行估计。为消除量纲影响和变量自身变异的影响,对各解释变量的指标数据进行了标准化。同时,为保证统计推断的有效性和可靠性,利用Bootstrap法来估计稳健的系数值及其置信区间,回归结果见表5。
(1)沿海城市经济发展水平与海洋经济效率无显著相关关系。通常认为,经济发展水平较高的地区,海洋经济效率也相应较高。既然海洋经济实质是陆域经济向海洋的延伸,陆域经济的发展基础和层次对海洋经济发展有着重要影响。然而,就我国沿海城市海洋经济效率而言,沿海城市的经济发展水平对其海洋经济效率的影响并不显著。
(2)海洋经济发展水平、环境保护力度对海洋经济效率具有正向影响。沿海城市海洋经济的发展水平每提高1个单位,海洋经济效率值的倒数减少5.769,这意味着沿海城市海洋经济的发展一方面带来了海洋经济效率的提升,另一方面海洋经济效率的提高又可以进一步提升海洋经济发展水平,从而在二者之间形成“循环累积因果效应”,故海洋经济发展水平正向促进海洋经济效率的提高。沿海城市环境保护力度每提高1个单位,海洋经济效率值的倒数减少4.607,即加强城市环境保护有助于海洋经济效率的提升。环境承载力作为经济发展的基础条件,加强环境保护能够提升资源利用效率和向先进生产方式的转变,因此应注重发展环保技术,提高沿海城市经济活动的环保水平。
(3)对外开放程度、环境污染对海洋经济效率具有负向影响。沿海城市外贸依存度每提高1个单位,海洋经济效率值的倒数提高7.480,表明对外开放程度越高反而不利于海洋经济效率的提升。这与通常的看法相反。原因可能来自,沿海城市对外开放程度越高,其开发力度也越大,从而海洋资源开发无序、无度、无偿的现象也越突出,从而导致海洋经济效率的下降。环境污染同样对沿海城市海洋经济效率具有负效应,表明城市环境质量的改善实际上有助于海洋经济效率的提升。
表5亦给出了传统两阶段DEA模型(即表5中Tobit模型2) 与考虑了环境因素的纠偏修正后的效率值的倒数(Y1)作为因变量的Tobit模型(即表5中Tobit模型1) 的回归结果。可以看出,各海洋经济效率影响因素的系数值的符号均未发生变动,然而,除了常数项外,各回归系数却不再显著。这是由于传统两阶段DEA方法中的第二阶段回归分析违背了独立性假设,从而使得Tobit回归模型的估计结果变得有偏和不一致,因此无法确定各个影响因素对海洋经济效率的真实效应。
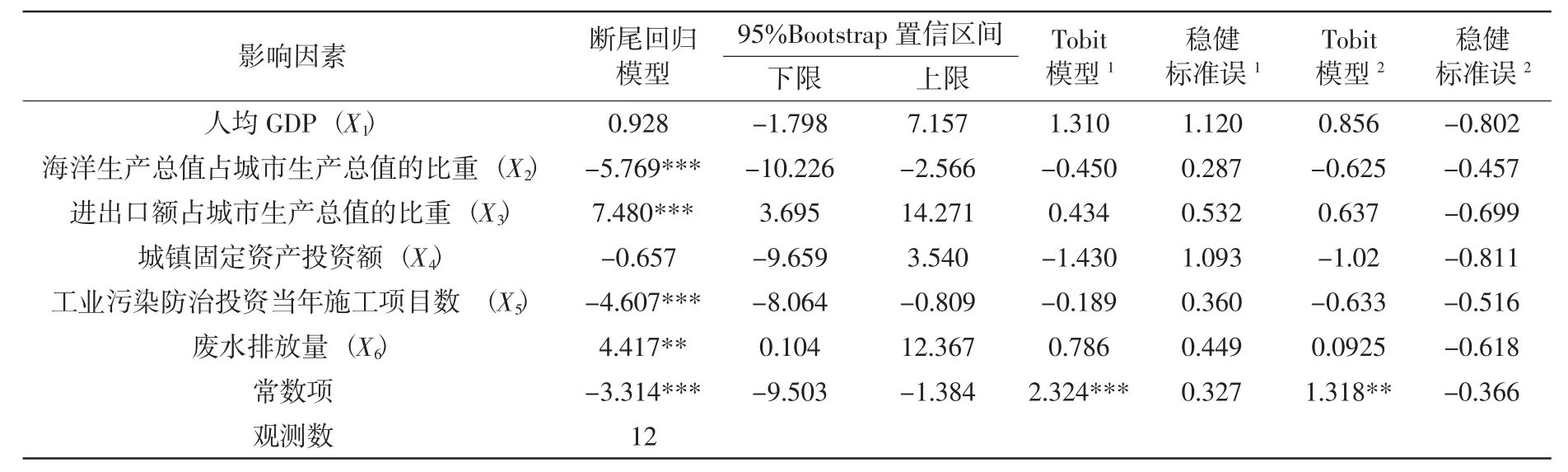
表5 沿海城市海洋经济效率影响因素的模型回归结果
4 结论与建议
由于传统DEA方法在效率评价上存在缺少统计推断、效率值易被高估的缺陷,本文运用基于自助抽样的DEA方法对我国12个主要沿海城市的海洋经济效率值进行了测算,并利用基于自助抽样的断尾回归模型对影响沿海城市海洋经济效率的因素进行分析,主要结论如下:
(1) 从我国12个沿海城市海洋经济效率的相对排名上来看,烟台、汕头、海口无论是在对传统DEA效率值进行纠偏修正后的稳健DEA效率值排名上还是在考虑了环境因素后的稳健DEA效率值的排名上均位居前列,而与之相对的是,经济更为发达的沿海城市如宁波、厦门在效率排名上反而位居后列。这表明,经济愈发达的沿海城市其海洋经济效率未必会更高。而进一步通过对影响沿海城市海洋经济效率的因素进行分析后发现,沿海城市的经济发展水平与海洋经济效率之间并不存在显著的相关关系。这反映出沿海城市陆域经济与海洋经济在发展过程中还存在着不平衡、不协调的现象,实现十九大报告中提出的建设海洋强国的战略目标,需要将陆域经济与海洋经济密切结合起来,坚持走“陆海统筹”之路。
(2)虽然沿海城市自身经济发展水平与其海洋经济效率无显著相关关系,但沿海城市海洋经济发展水平对海洋经济效率具有正向影响。这表明沿海城市海洋经济的发展与海洋经济效率具有“循环累积因果效应”,即:沿海城市海洋经济的发展带来海洋经济效率的提升,而海洋经济效率的提高反过来进一步提升海洋经济发展水平。同时,外贸依存度高的沿海城市海洋经济效率实际更低。这表明外贸依存度大、对外开放程度高的沿海城市的海洋资源可能存在过度开发的问题。海洋资源开发上存在的无序、无度、无偿的现象抑制了海洋经济效率的提高。因此,沿海城市要十分重视海洋资源承载力的评价与分析,综合考量经济发展与海洋资源之间的协调关系,从而实现海洋经济的可持续发展。
(3) 环境污染同样不利于海洋经济效率的提升。这意味着,沿海城市环境质量的改善实际上有助于提高沿海城市的海洋经济效率。实际上,本文研究也发现,沿海城市的环境保护力度对海洋经济效率的提高具有正效应。发展海洋环境保护技术有助于提升海洋资源利用效率和向先进生产方式的转变,从而提升沿海城市海洋经济效率。这一结论与人们通常认为的海洋经济发展与海洋生态保护之间存在冲突的观念相悖,表明沿海城市海洋经济发展与生态环境之间存在着协调发展的关系。沿海城市要发展绿色经济和推动海洋经济的绿色发展,提升海洋经济效率并促进海洋经济快速以及高质量的发展。

