限制空间氮气置换过程分析与优化

郑震宇，邓佳佳，谭金元，卢金树，薛大文

(浙江海洋大学 港航与交通运输工程学院，浙江 舟山 316022)

0 引 言

当今世界环境恶劣、污染严重，而天然气因具有燃烧高效、安全环保等优点被大量使用。由于LNG的产地和需求地不匹配，在两者间需要有运输环节。运输时，不可避免地会遇到新液舱或检修后的液舱，这就需要对液舱进行气体置换。置换的目标是将液舱内氧气质量分数降至低于2%，以防止LNG首次进入储罐时与空气混合引起爆炸[1]。置换气体通常采用惰性气体，常见的惰性气体有二氧化碳、水蒸气和氮气，其中氮气是较主要的惰性气体，应用广泛，不仅适用于各种温度，而且对管道与装置的要求也没有前两种气体苛刻，是工业生产中较为理想的惰性气体[2]。由于置换过程都是在液舱中进行的，因此，研究限制空间内的气体置换作业过程有利于优化液舱的气体置换设计方案，具有很大的工程意义。

常用的气体置换方法主要包括：混合置换、无混合置换、真空置换和加压置换等4 种置换方式[3-4]。混合置换(又称为推移式置换)以其易于实现、工作效率高的优点被广泛采用。黄光容等[5]发现增加富氮气体流量、提高富氮气体中氮气的含量可缩短惰化时间。KURLE等[6]建立了一个飞机燃油箱惰化系统，结果表明，在相同的操作条件下，当惰性气体流量增加时，所需惰化时间减少。王志伟[7]对燃油箱惰化过程进行研究，发现完成惰化所需氮气气体量与进气方式和载油率有关。宋洋[8]经研究得出气体入口速度越快，液货舱惰化速度越快。然而，这些研究很少提及达到推移式置换条件时所需的进口面积、形状和流速带来的影响。为此，本文采用CFD数值仿真方法，建立二维模型，通过改变进气口径大小和进气速度，对长为10 m、宽为2 m的限制空间进行气体置换数值模拟，探究进口面积、形状和流速对推移式置换的影响。

1 模型

1.1 物理模型

某LNG液舱简化图如图1所示，该液舱长38 m、宽50 m、高10 m[9]。在液舱顶部设有一根水平的进气管，进气管上每隔相同距离设有气孔。在进行液舱惰化时，氮气从气孔自上而下喷入，整个液舱中间部分可近似简化为由无数个含有气孔的矩形连接而成，相邻矩形的结构、流场相似，可忽略矩形间的影响。取其中一个矩形进行研究，如图2所示。为便于研究，简化后的限制空间长为10 m、宽为2 m。

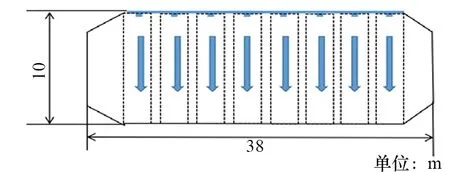
图1 LNG液舱物理模型

图2 模型简化

初始时，液舱内部充满温度为300 K，环境压力为0 Pa的空气。充入纯氮气进行置换，通入氮气温度为300 K。置换的目标是使空间内氧气质量分数低于2%(为便于研究，忽略空气中其他稀有气体)。氮气及氧气的物性参数如表1所示。

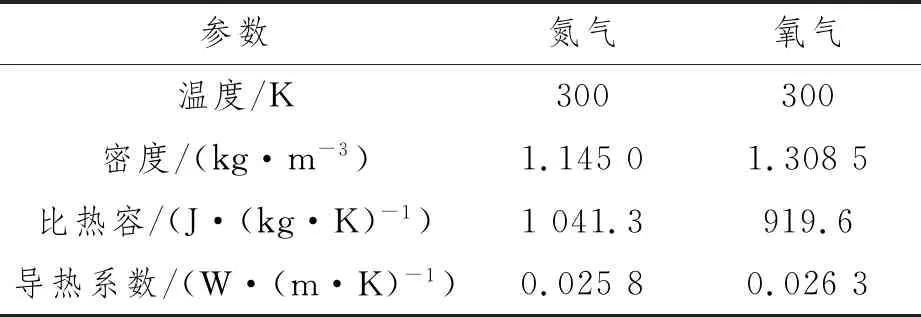
表1 氮气及氧气物性参数

1.2 数学模型

由于实际置换过程较为复杂，现作出如下简化：

(1)实验舱为绝热系统，暂不考虑系统的热耦合。

(2)不考虑限制空间内的泄漏情况，并将限制空间内空气的成分进行简化：空气由21%(体积分数)的氧气和79%(体积分数)的氮气组成。

(3)在气体置换过程中，所需控制方程主要包括质量方程、动量方程、组分控制方程和标准k-ε湍流模型[10]。

1.3 模型设置

利用Gambit 2.4划分网格，其中限制空间内流体区域设置为流体(Fluid)，网格尺寸为12 mm，Gambit划分网格数量为1.25×105个。

利用Fluent 15.0进行模拟，选择2D计算器。模型设置选择能量方程、标准k-ε湍流模型。选择重力场，x方向重力加速度的数值为9.81 m2/s。

设置边界条件和区域条件。将置换气体进口设置为速度进口，组分为纯氮气，出口设置为压力出口，对称边界条件。在Solution Methods中，压力速度耦合选择SIMPLE。在Solution Controls中，压力、密度分别取0.3 Pa、1 g/cm3，Momentum、Turbulent Kinetic Energy、Turbulent Viscosity、Energy分别取0.7 kg·m/s、0.8 m2/s2、1 Pa·s、1 J。

对全区域进行初始化，其中速度为0 m/s,压力为0 Pa，温度为300 K，氧气体积分数为21%。不设置临界收敛值，每个时间步长为0.001 s，共计算50 000步，每时间步迭代20次。

2 模型验证

2.1 计算模型验证

对实验舱[11]的气体置换过程进行模拟，通过对比模拟结果与试验结果验证模型的准确性。实验舱为矩形，长为2.20 m，宽为0.92 m，高为1.22 m。进气口采用速度入口，出气口采用压力出口。在计算过程中，监测舱内氧气平均质量分数值，将其与试验结果进行对比，结果如图3所示，从图中可以看出计算结果与试验结果吻合较好。

图3 计算结果与试验结果对比

2.2 网格无关性验证

理想的气体置换氧气质量分数云图如图4所示，云图大致可分为3层。在进行气体置换过程中，氮气和空气不可避免地会发生气体扩散，为清晰表达置换效率，理清对流和扩散两种机理在置换过程中的作用，取氧气质量分数为10.5%(空气和纯氮气含氧量中间值)等值面代表对流推移置换效率，入口到该面的体积与实际充入氮气量一致，进一步取氧气质量分数2.0%等值面(置换目标)及其关于10.5%等值面的对称面即氧气质量分数19.0%等值面，2.0%与19.0%质量分数等值面之间的距离(厚度)代表扩散带来的影响。

图4 氧气质量分数等值面示例

数值模拟计算的基本原理是将计算域离散成多个控制体，并积分得到代数方程，迭代计算得到数值解。采用CFD软件对限制空间的模型进行建模并划分网格，进气时间为3 s。经过网格无关性验证，网格数量对计算结果影响很小，为减少计算误差，取均方根σ的误差率在2%以内，计算结果如表2所示。

表2 3 s内网格数量敏感性分析

表2中：0.8万网格代表网格质量为“粗”；3万网格代表网格质量为“中”；12万网格代表网格质量为“细”；50万网格代表网格质量为“精”。综合考虑计算经济性和计算准确性，取网格数量为126 246(12万)个用于计算。

2.3 时间步长敏感度分析

时间步长是指前后两个时间点之间的差值。在模拟系统的时间响应时往往需设定时间步长，时间步长的大小一般取决于系统属性和模型的目的。由于对流层高度变化都很小(几乎没有改变)，因此为了更直观地比较，在时间步长分析中只分析扩散带厚度的变化。3种不同时间步长计算结果如图5和表3所示。为减少运算量、节约计算资源，时间步长取0.001 0 s。

图5 时间步长敏感度分析结果对比

表3 3 s内时间步长敏感度分析

3 气体置换模拟及机理分析

3.1 无量纲参数

为更好地显示不同速度下置换所需的氮气体积，引入无量纲时间τ，其定义为

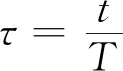
(1)

式中:t为原始时间，s；T为周期，即充入氮气体积等于置换空间体积所需的时间，s。

当τ=1时，代表充入氮气体积等于限制空间体积；当τ>1时，代表充入氮气体积大于限制空间体积。

3.2 基准方案结果分析

取口径大小占限制空间宽比例为20%、30%和40%，初始速度暂设定为2 m/s。选取无量纲时间τ为0.3、0.6和0.9的氧气质量分数云图进行对比分析，如表4所示。

表4 不同进气口直径下氧气质量分数分布

判断推移式置换的标准为氧气质量分数各等值面随时间的变化平稳移动。当进气口大小占比为20%时，限制空间氧气云图显示内部气体氧气质量分数分布杂乱无章，充入氮气与空气明显发生混合，不符合推移式置换要求。在进气口大小占比为30%～40%时，氧气质量分数云图显示对流与扩散分界线明显，说明增大进气口直径容易实现推移式置换。

进气口直径占比为20%、30%和40%的对流层与扩散层变化如图6所示。20%工况对流层随着时间的推移变化较小，始终维持在空间顶部，无法形成平整的质量分数等值面。相对来说，进气口直径占比为30%和40%的对流层和扩散层运动规律明显。然而在实际工程应用中，进气口的直径都较小，因此考虑保持小进气口，并以层层扩大的进气方式完成限制空间的气体置换。

图6 氧气质量分数随时间变化的坐标高度

4 优化方案及机理分析

4.1 优化结果

在限制空间上方加装2个矩形嵌套，进气口占矩形宽的一定比例，长度为1 m，进气方式为上进下出，进气速度初步设为2 m/s,其余条件不变。当进气口直径占比为20%时，优化效果明显。优化前后氧气质量分数云图如表5所示。

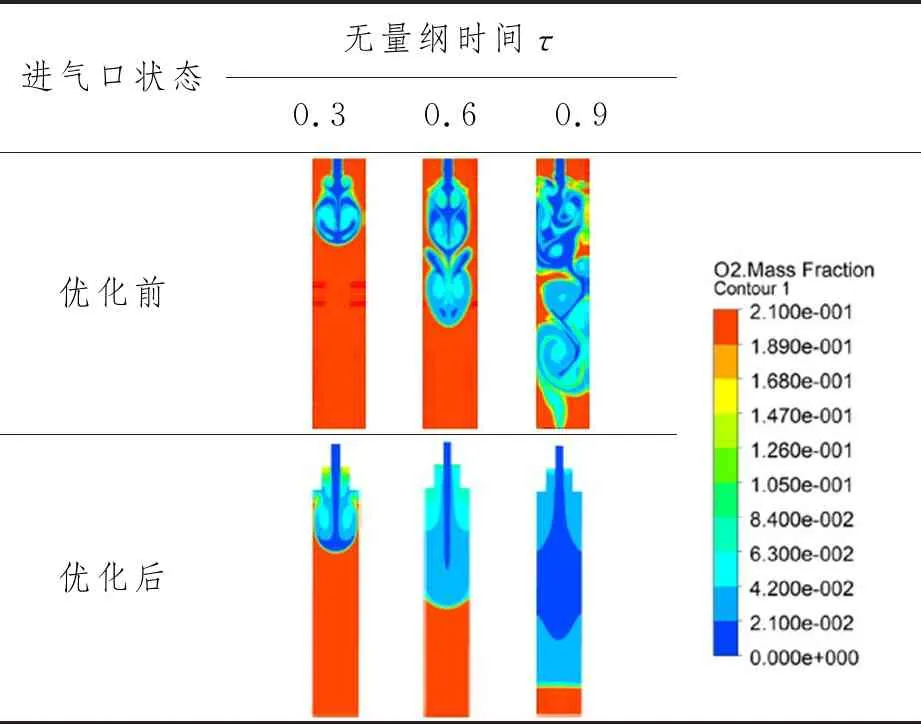
表5 优化前后氧气质量分数分布

从表5可知：优化后，20%入口比例工况基本实现推移式置换，优化效果明显。由于空间为对称边界，选取中线靠右侧半个计算区域进行优化前后速度分布对比，以分析优化前后置换效率改变的原因。图7所示为距进气口0.5 m、1.0 m、2.0 m和3.0 m的平面位置。无量纲时间为0.3、0.6和0.9时的平面速度标准偏差对比如图8所示。由图8可知：优化后各平面的速度标准偏差均有所降低，且0.5 m平面速度标准偏差最大，最具代表性，因此后续均选取0.5 m平面进行进一步分析。

图7 不同平面位置

图8 优化前后距进气口不同位置速度标准偏差对比

4.2 优化机理分析

图9为优化前后距进口0.5 m平面的速度分布对比图。从图9可以看出：不同时刻优化后，0.5 m平面速度分布曲线比初始方案更平坦，整体呈“乁”字形；优化后速度上拐点提前约50%，说明同一位置优化后速度下降更快；优化后无明显的速度下拐点，中间有段区域优化后速度比优化前大，但整体曲线后半段较为平坦，说明优化后整个平面速度场更均匀，有利于形成推移式置换。图10为对应速度分布标准偏差对比，横坐标为优化前后无量纲时间0.3、0.6和0.9时刻。从图10可以看出，优化后0.5 m平面速度分布标准偏差平均降低8.5%，最高降低10.8%，最低降低6.6%。

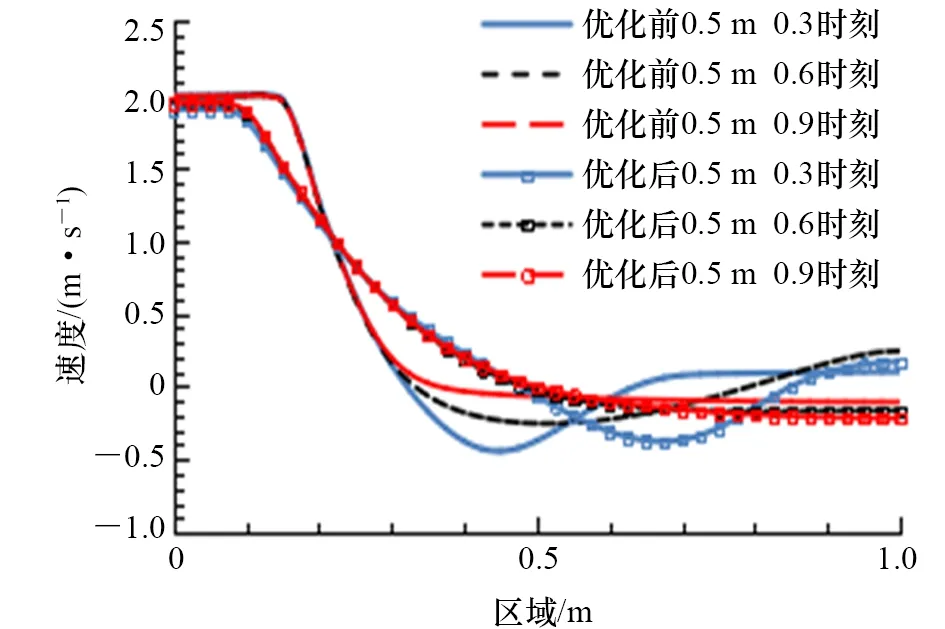
图9 优化前后距进口0.5 m处速度分布对比

图10 优化前后距进口0.5 m处速度标准偏差对比

图11和图12是不同时刻优化前后0.5 m平面氧气质量分数分布曲线和氧气质量分数分布标准偏差对比图。从图11可以看出，优化后0.5 m平面质量分数分布明显较优化前均匀，优化后氧气质量分数拐点同样提前约50%，说明同一位置优化后氧气质量分数提前升高。在曲线后半段，优化后质量分数小于优化前并且曲线较平坦，说明此时整个平面质量分数梯度小，平面质量分数较为均匀。从图12可以看出，优化后0.5 m平面氧气质量分数分布标准偏差平均降低124.3%，最高降低210.2%，最低降低44%。

图11 氧气质量分数分布

图12 氧气质量分数标准偏差

4.3 优化结果分析

优化方案与原始方案完成置换所需的无量纲时间对比如表6所示。在不同速度时，优化方案无量纲时间均比基准方案小，差异较大的20%无量纲时间相差在1.58%～11.21%，说明方案经过优化后明显节省氮气量，具有一定的工程意义。

表6 优化前后不同进气速度无量纲时间对比

在优化方案下，不同进气速度氧气质量分数分布如表7所示。当速度增大时，空间内易形成漩涡，导致耗氮量增大，说明进气速度低时经济性好。

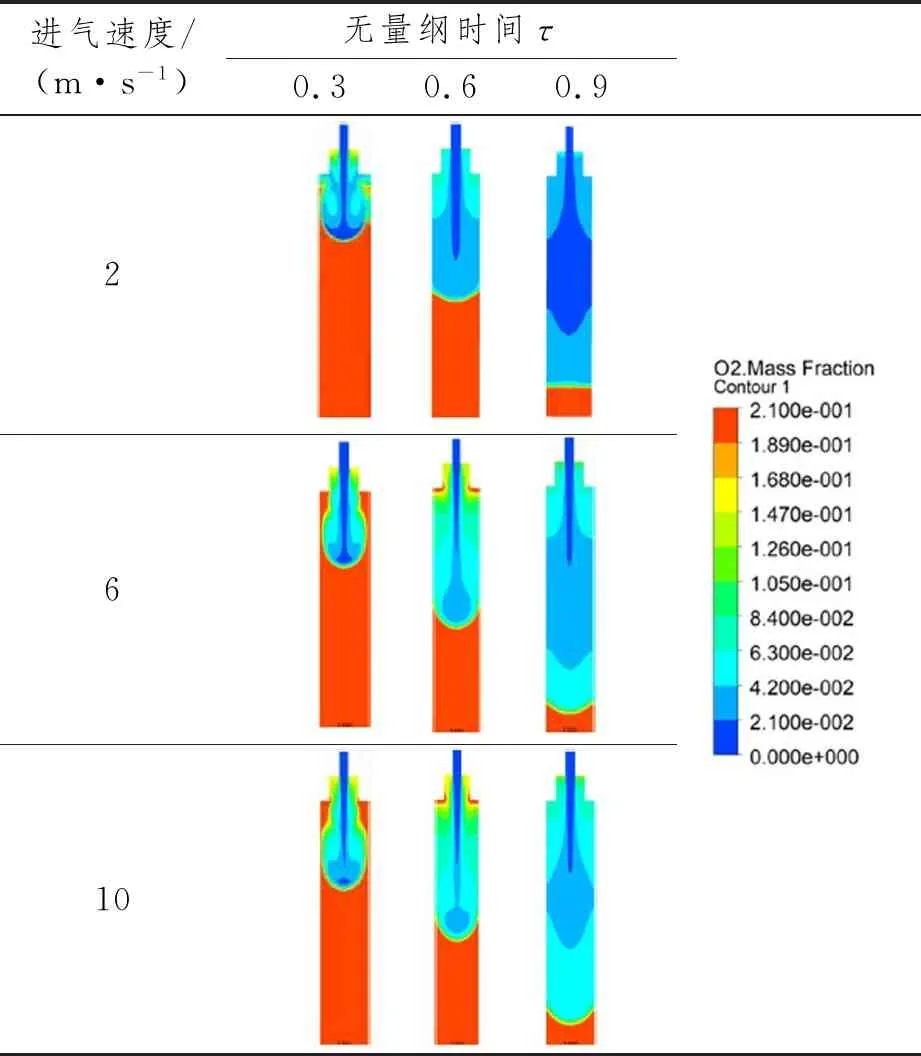
表7 优化方案下不同进气速度氧气质量分数分布

在实际置换过程中，最理想的方案是以最少的耗氮量和最短的时间完成置换。优化方案实际完成置换所需时间如表8所示，当进气速度为2 m/s时，优化效果最明显，可节省17%的时间。因此，优化方案可节省实际工程时间，具有可行性。

表8 优化前后不同进气速度实际置换时间对比

5 结 论

基于CFD方法对限制空间氮气置换过程进行数值模拟，分析不同进气方式对置换效果带来的影响，提出相关优化建议。得到结论如下：

(1)基于CFD方法计算限制空间内的平均氧气质量分数与文献试验中的数据吻合较好，说明该模型能够较准确地模拟限制空间内氮气置换过程。

(2)进气口越大越容易实现推移式置换；优化方案与原始方案相比可减少约1.58%～11.21%的氮气量，最多可缩短17%的置换时间，具有更好的经济性。

(3)优化方案中减慢进气速度可减少耗氮量，但会延长置换时间。因此，根据目标不同可选择不同的进气速度。

根据模拟计算结果，对置换过程各参数进行分析，为提升置换作业过程的经济性和安全性，提出如下建议：

(1)在实际置换作业过程中，将氮气进气口形状改装成矩形嵌套可减少置换所需的氮气量。

(2)虽然适当提升进气速度可减少置换时间，但是流速太高会使管道内的焊渣等可移动物体在高速气流携带下运动，易与管道碰撞，产生电火花[12]，因此进气流速控制在2～5 m/s为宜。