机载动能拦截弹大气层内助推上升段自适应设计方法
赵友铖,关皓天,程 林,张庆振
(北京航空航天大学,北京,100191)
0 引 言
动能拦截弹是一种由助推火箭和作为弹头的动能杀伤飞行器(Kinetic Kill Vehicle,KKV)组成,借助KKV高速飞行时所具有的巨大动能,通过直接碰撞摧毁目标的武器系统,在高空拦截防御体系上有着重要的应用价值[1,2]。动能拦截弹的拦截目标一般为弹道导弹与空间目标,目前主要由地基或海基发射,机载发射能大大增加作战半径,提高作战灵活性与机动能力[1~3]。
但机载发射与技术相对成熟的地基、海基发射相比,自身也存在诸多问题。首先,由于机载发射的灵活性,拦截弹助推上升段的初始状态、飞行剖面存在很强的不确定性,且飞行过程中的气动环境变化剧烈,拦截弹本身质量、转动惯量、质心位置在不断变化,传统线性控制器已不能满足拦截弹在飞行过程中的姿态快速调整性能要求。设计能满足任务需求的自适应姿态控制器是本文的一个研究目标。其次,受载机性能所限,拦截弹的初始弹道倾角较小,爬升能力受到很大限制,而目标一般处于大气层外,拦截弹需尽快飞出大气层进行主动段中制导,给拦截弹助推上升段设计带来很大挑战。目前的助推上升段设计方法主要以地基发射为条件[4~6],对机载发射的研究很少。机载发射拦截弹要实现最快爬升,以最大攻角飞行即可[7],但的值主要由气动力矩与执行机构幅度限制决定,而机载动能拦截弹的大飞行包络与复杂的气动环境导致的变化较为剧烈,如何在大包络与干扰摄动下设计助推上升段从而实现快速爬升,是本文的研究重点。
针对上述问题,以动能拦截弹的一级助推段为研究对象,提出机载动能拦截弹的一种自适应姿态控制器设计方法与一种上升段指令设计方法。
1 机载动能拦截弹上升段数学模型
动能拦截弹在上升段由助推火箭将拦截器运送出大气层。在建立动能拦截弹上升段模型前,首先进行合理的建模假设[6]:
a)载机发射拦截弹时一般处于目标运动平面内,故研究拦截弹上升段时忽略横侧向运动,仅考虑纵向模型;
c)由于助推上升段时间比较短且处于大气层中,忽略地球自转的影响,认为;
d)忽略火箭内部介质相对于弹体流动以及推力矢量执行机构所引起的哥氏力与全部附加力矩。
拦截弹由助推火箭(两级)与上面级(动能拦截器)组成。其中助推火箭不采用气动舵,执行机构为摆动喷管,采用十字形结构。助推火箭推力在弹体坐标系(苏氏)上可表示为

在发射系下建立动能拦截弹上升段数学模型[6]:

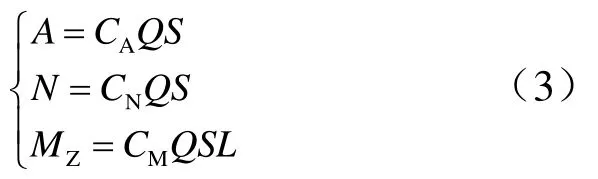
2 基于ESO的自适应姿态控制器设计
拦截弹姿态控制器(Extened State Observe,ESO)设计采用内外环结构,其中内环角速率采用扩张状态观测器+PID控制器,利用扩张状态观测器的干扰补偿能力补偿拦截弹在不同工作点下的扰动影响[5];考虑到上升段设计时气动力、气动力矩的影响较大,故外回路选择攻角作为控制量更加方便。控制器结构如图1所示。
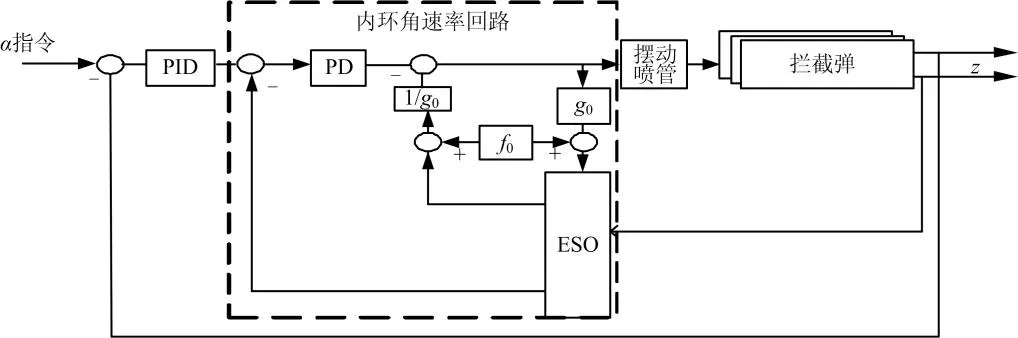
图1 拦截弹自适应姿态控制器结构Fig.1 Interceptor Adaptive Attitude Controller Structure
飞行器内环姿态控制器跟踪姿态角速度信号,内环角速度动力学模型可以表示为如下形式:

结合式(2)中绕质心动力学方程可得:
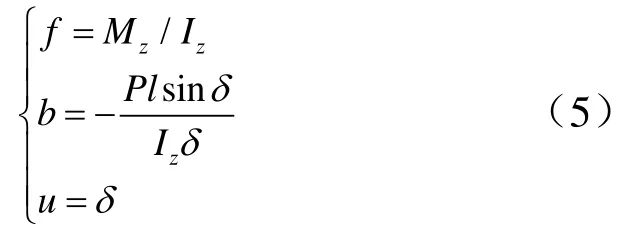

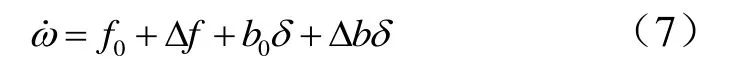
即:

对俯仰角速率回路配置二阶线性扩张状态观测器可得:
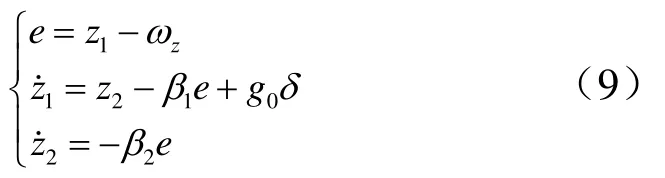


利用扩张状态观测器进行实时估计补偿扰动作用,从而将原非线性系统补偿为线性积分串联型系统。结合PD控制,可以得到系统内环控制器输出为
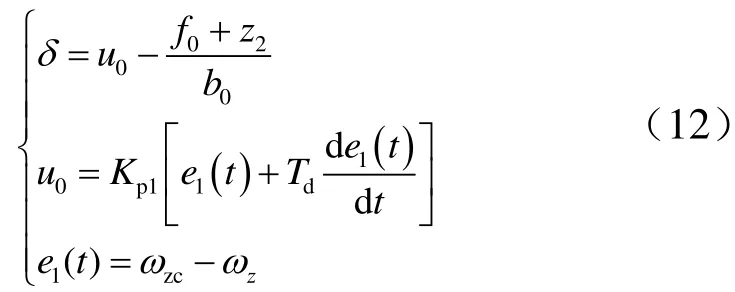
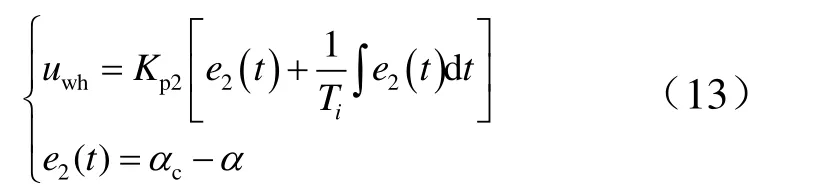
通过仿真验证控制器性能。取初始状态为典型发射状态:H=10 km,=30°,=350 m/s,=0°。
输入方波攻角信号,仿真结果如图2、图3所示。
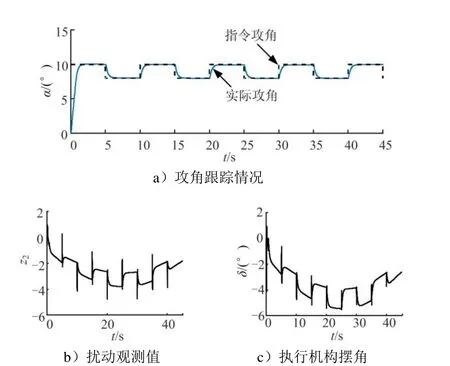
图2 拦截弹攻角跟踪、扰动观测值与执行机构摆角变化曲线Fig.2 Angle of Attack, Disturbance Observation and Rudder Angle of the Interceptor
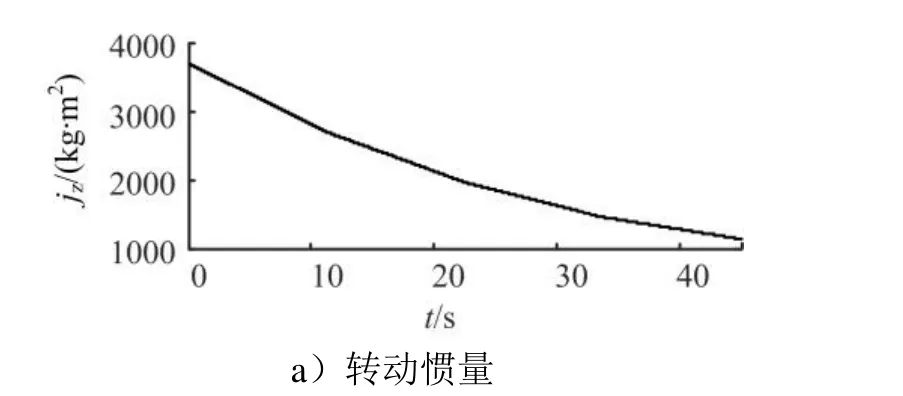
图3 拦截弹转动惯量、质心位置、高度、速度变化曲线Fig.3 Inertia, Centroid Position, Height and Speed of the Interceptor
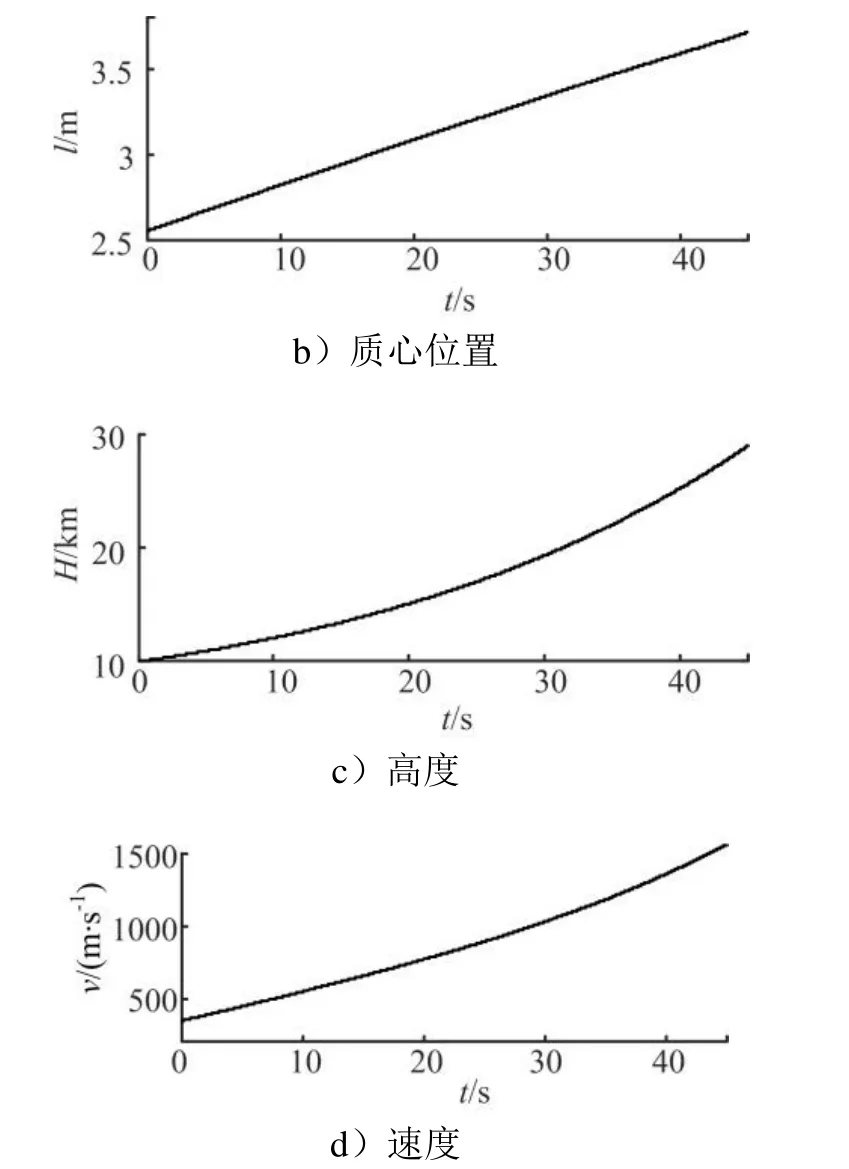
续图3
从图2、图3可以看出,ESO能有效观测补偿系统不确定性,系统在拦截弹本身参数与工作点变化剧烈的情况下能够快速跟踪方波信号(10°阶跃响应调节时间为1.2 s,跟踪方波调节时间小于1 s),无超调,基本无稳态误差。控制器性能良好,可以基于此控制器进行助推上升段设计。
3 机载动能拦截弹上升段自适应设计方法
本文提出一种基于实时反馈的机载动能拦截弹上升段自适应指令在线生成方法。在确定设计原则的基础上,进行机载动能拦截弹上升段设计。
3.1 设计原则
借鉴陆基发射远程火箭飞行程序角设计原则,考虑到实际需求,提出机载动能拦截弹上升段设计约束如下[6]:
a)飞行程序角应是时间的连续函数;
3.2 最大允许攻角的确定
机载拦截弹助推上升段的设计目的是设计能使终端高度最高的指令攻角序列。为此需要得出拦截弹在飞行过程中攻角允许的最大值。

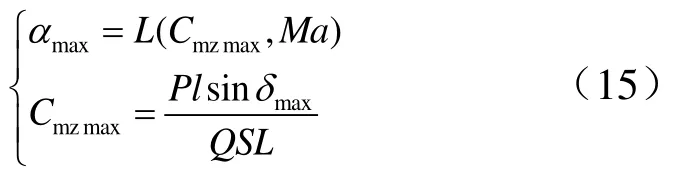
3.3 自适应上升段设计方法
针对机载拦截弹的上升段,可通过离线设计方法得到一条在固定发射状态的快速爬升攻角序列,但是应对比较大的大气扰动、发射初始状态偏差时,一条固定的程序角序列不能满足任务需求。基于不依赖精确模型、仅根据拦截弹自身能力实现快速爬升的设计思想,本文提出一种基于实时反馈的机载动能拦截弹上升段自适应指令在线生成方法,总体结构如图4所示。
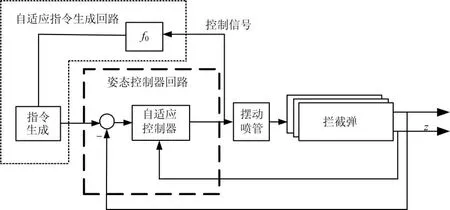
图4 上升段自适应指令在线生成方法结构Fig.4 Ascending Segment Adaptive Instruction Online Generation
针对气动环境与初始状态不确定性强的特点,对工作攻角在线实时解算。攻角指令在线生成公式为
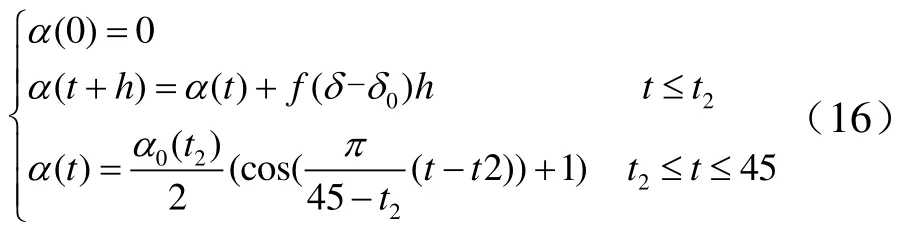
基于以上选取原则,采用fal函数[6]并加以改进,写出表达式如下:
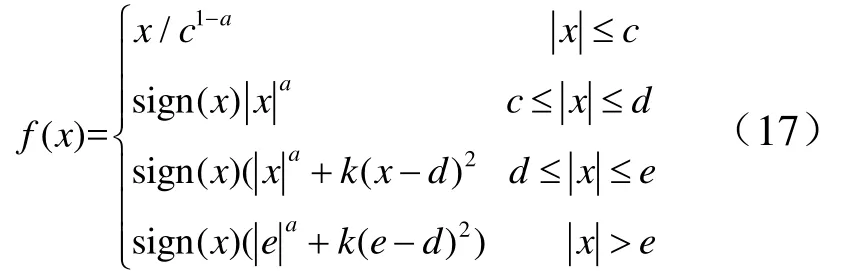
以典型发射状态式(15)为初始状态,采用自适应指令在线生成方法进行仿真,仿真结果如图5、图6、表1所示。从图15、图16可以看出,自适应指令在线生成方法的上升段终端参数与离线程序角终端参数基本相同,且执行机构摆角基本稳定在工作点,故可以认为在标称情况下拦截弹实现了约束内的快速爬升。
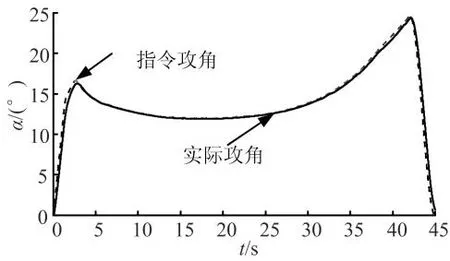
图5 自适应在线指令生成与跟踪变化曲线Fig.5 Adaptive Online Command Signal Generation and Racking

表1 终端参数Tab.1 Terminal Parameter
4 综合仿真分析
机载动能拦截弹助推上升段设计方法须要适应机载发射的不确定性与外界扰动。本章通过进行过程参数拉偏与初始状态拉偏,验证上升段设计方法的鲁棒性与自适应能力。拉偏情况如表2所示。
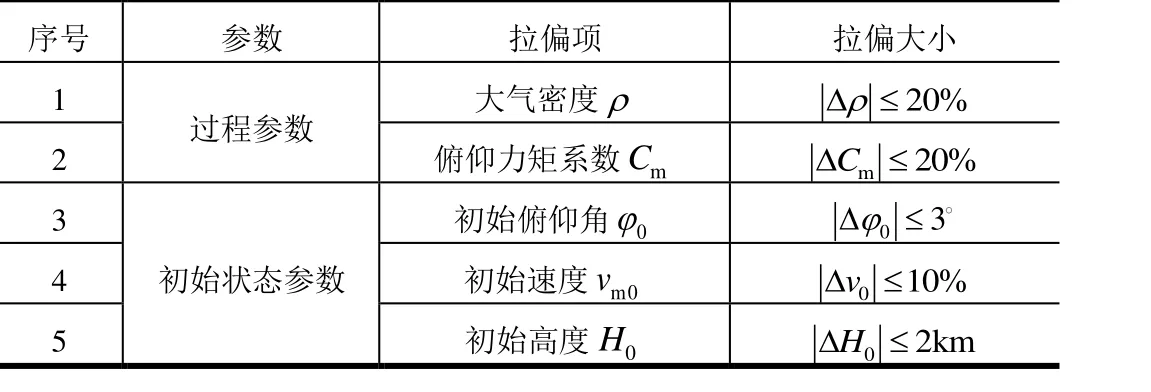
表2 参数拉偏值Tab.2 Parameter Bias Value
以典型发射状态为初始状态,分别使用离线设计所得指令与自适应指令在线生成方法在参数拉偏的情况下进行仿真,仿真结果如图7、图8所示。
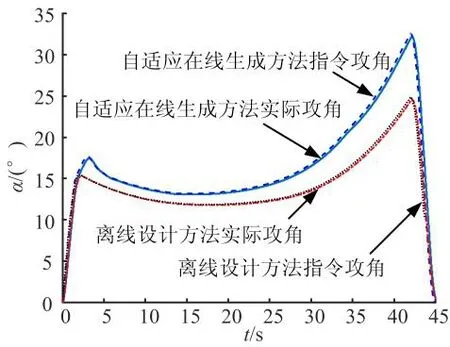
图7 过程参数负拉偏仿真结果曲线Fig.7 Process Parameter Negative Pull-Off Simulation Result Graph
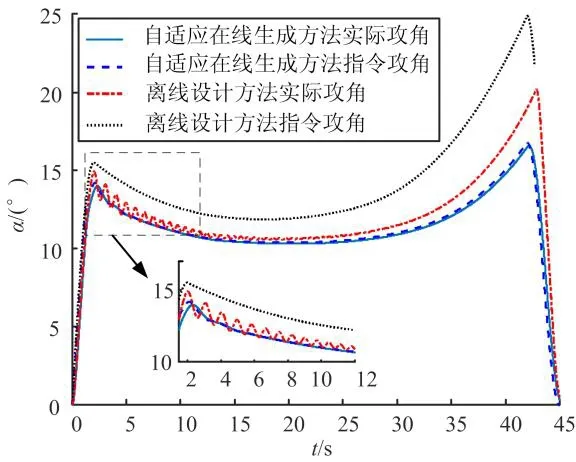
图8 最坏发射状态拉偏仿真结果曲线Fig.8 Worst Emission State Simulation Result Graph
从图7、图8可以看出,自适应指令在线生成方法相比离线程序角,能够适应不同的发射状态偏差,对环境扰动具有较强的鲁棒性,且能在发射环境有利时更充分地利用自身爬升能力。
5 结 论
本文针对机载动能拦截弹助推上升段设计中存在的问题,开展自适应姿态控制器设计方法研究与机载动能拦截弹助推上升段指令设计方法研究。主要有:
a)在合理假设的基础上建立机载动能拦截弹助推上升段动力学与运动学模型;
b)设计了基于ESO的自适应姿态控制系统;
c)提出了基于实时反馈的机载动能拦截弹助推上升段自适应指令在线生成方法。
仿真结果表明:基于ESO的自适应姿态控制器能够适应大包络飞行;自适应指令在线生成法具有良好的自适应能力与鲁棒性,适合机载动能拦截弹不确定性强、外界扰动剧烈的特点,具有一定的工程应用价值。

