一种姿控推进剂加注量精确计算方法
鄢青青,彭宗尧,许秀清
(西昌卫星发射中心,西昌,615000)
0 引 言
某型姿控动力系统使用单组元推进剂,主要为运载器非主动力飞行段的推进剂沉底、姿态控制和轨道修正提供长时间、方向可控的微小推力[1,2]。该型姿控动力系统的推进剂采用耐低温、催化分解反应剧烈的肼类混合物[3~5],其加注方式主要是气体挤压式加注。该加注方式具有简单、安全、启停控制快速准确等优点。但由于目前主要采用贮罐去皮后的称重减少量作为目标加注量来控制加注停止,未考虑贮罐增压气体的质量,导致加注量的取值不够精确,实际加注量一般大于目标加注量。而精确的取值方法不但有利于降低姿控加注量的误差范围,对姿控发动机总冲的精确计算和飞行轨道与姿态的精确设计也有一定的贡献。
本文根据姿控加注的原理,分析目前两种加注量取值方式存在的不足,基于气液等体积替换假设推出了实际加注量的计算公式和在给定目标加注量时的加注控制量计算公式,并用历史数据验证了该方法的正确性,分析了压力与温度误差对加注量的影响,为姿控推进剂实现精确加注提供了技术支撑。
1 姿控加注原理及加注量取值方式的不足
姿控加注的原理如图1所示。
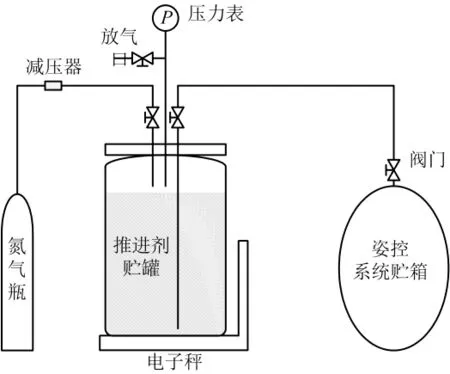
图1 姿控加注原理简图Fig.1 Principle Sketch of Propellant Filling for Attitude Control Thruster
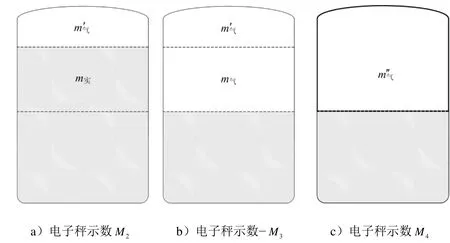
图2 推进剂贮罐的电子秤示意Fig.2 Displaying Weight of Electronic Scale for Propellant Tank
a)取为目标加注量时:
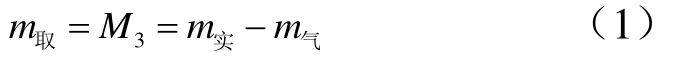
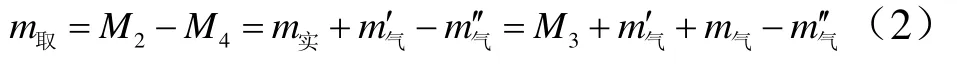
上述两种取值方式的优点是均在维持管路充填状态不变的情况下计算加注量,避免了管路充填量差别和吹回过程的残留、蒸发等带来的误差。其中第1种取值虽然达到了目标加注量,但与姿控贮箱内实际加注的推进剂量不符,第2种取值与实际加注量和目标加注量均不相符。即两种取值方式都无法使取值、实际加注量、目标加注量三者完全相等,均会导致实际加注量与目标加注量之间的误差。
2 基于气液等体积替换的加注量计算方法
假设贮罐中的推进剂是充分混合、质地均匀的,且在加注过程中基本不蒸发或蒸发量可忽略不计;不考虑氮气在推进剂表面的溶解、反应,进入贮罐的氮气按理想气体[6]处理;增压压力恒定不变。
2.1 进入姿控贮箱的推进剂体积

由式(1)、式(2)可知:

当推进剂为混合均匀的液体,贮罐中氮气为理想气体,不考虑氮气溶解于推进剂中时,可认为取出的推进剂后所留下的体积用同体积、压力为的氮气充满,则等价于用的真空容器对气体进行称重(见图3),增加的气体质量应为其绝对压力质量:

代入式(4)得:
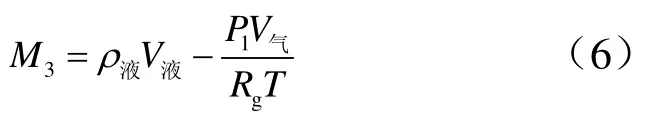
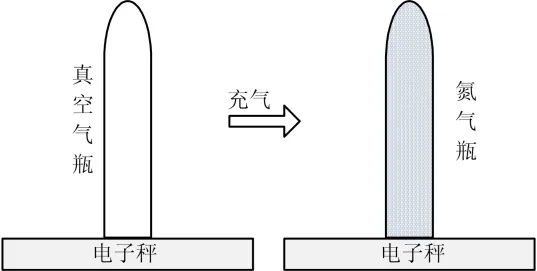
图3 真空法气体称重原理Fig.3 Gas Weighing Principle Based on Vacuum Method
进入姿控贮箱的推进剂的体积为
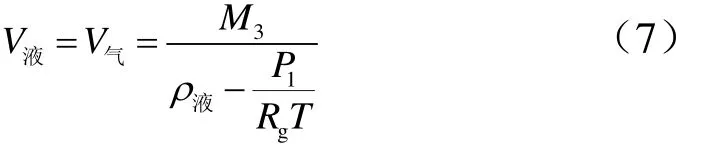
2.2 加注控制量的值
根据式(7),可得推进剂的实际加注量:
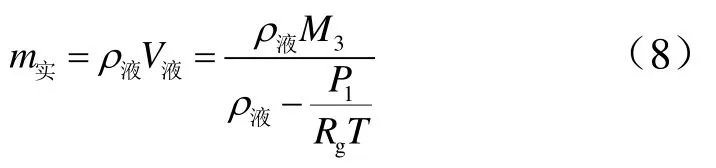
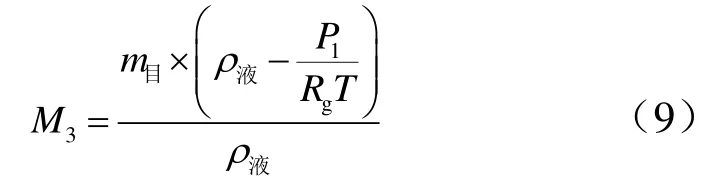
即在加注流程不变的情况下,根据目标加注量、推进剂的化验密度、增压压力、氮气温度,可得到在控制加注停止时的贮罐去皮后的减少量,以达到间接精确控制加注量的目的。
3 算例分析
3.1 加注量计算模型验证
某次历史加注中,采用式(2)进行加注量取值,其目标加注量为80 kg,增压的表压力0.1 MPa,当地大气压0.081 MPa,推进剂及氮气温度均为20 ℃,推进剂(单推-3)的密度[5]为1.112 g/cm3,加注前的贮罐气枕体积为0.01 m3,可根据式(2)和式(8)来验证该加注量计算方法的准确性。
首先,考虑等体积空气浮力后计算加注前贮罐的气枕气体质量:

根据式(8)得到进入贮箱的推进剂实际质量


根据式(2)计算最终的加注量取值:
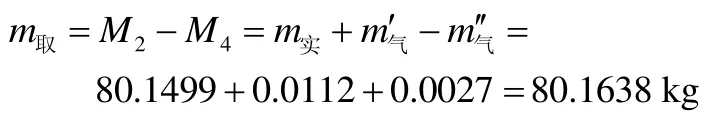
考虑到加注过程中,贮罐内的压力应稍低于0.1 MPa,使计算结果与历史加注实际取值80.16 kg偏差 0.0038 kg。如取贮罐内压力为 0.096 MPa时,=80.1600 kg,与历史数据实际取值相同。
同时,根据式(9),如果目标加注量为80 kg,则在实际加注过程中,应控制为79.8504 kg;取贮罐内压力为0.096 MPa时,应控制为79.8537 kg。
3.2 加注量误差分析
姿控推进剂加注过程中,减压器的调压误差、压力表的读数误差、电子秤的读值误差、氮气及推进剂的温度误差、推进剂的密度误差等均会导致和的计算误差。电子秤读值误差为仪器自动取值精度误差,其他误差则可归结为两类误差,即气体压力误差和温度误差。
a)气体压力误差影响。
气体压力误差在计算中主要表现为推进剂贮罐内的增压气枕压力误差,由式(8)、式(9)以及 3.1节可知,加注量取值为阶导数可得:
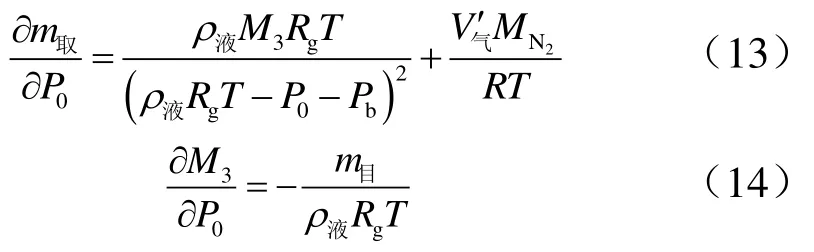
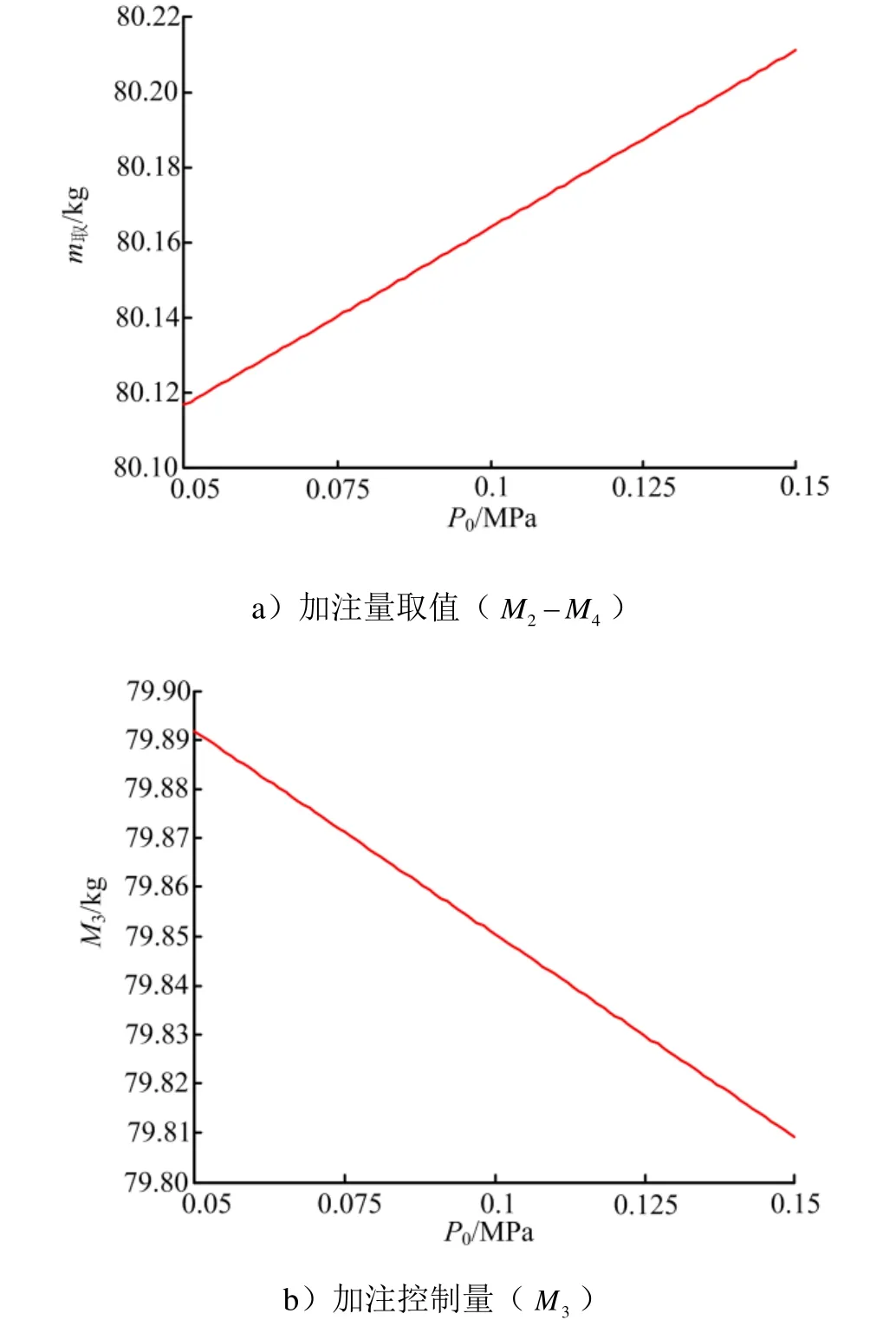
图4 加注量取值与加注控制量随变化曲线Fig.4 Curve of Filling Quantity and Filling Control Quantity Changing with
b)温度误差影响。
温度误差表现为推进剂和氮气的密度与体积误差,其中推进剂液体的体积误差暂忽略不计,气体体积受贮罐中气枕容积限制,推进剂(单推-3)的密度按如下方式获得[7]:
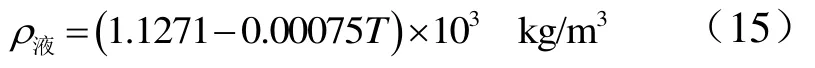
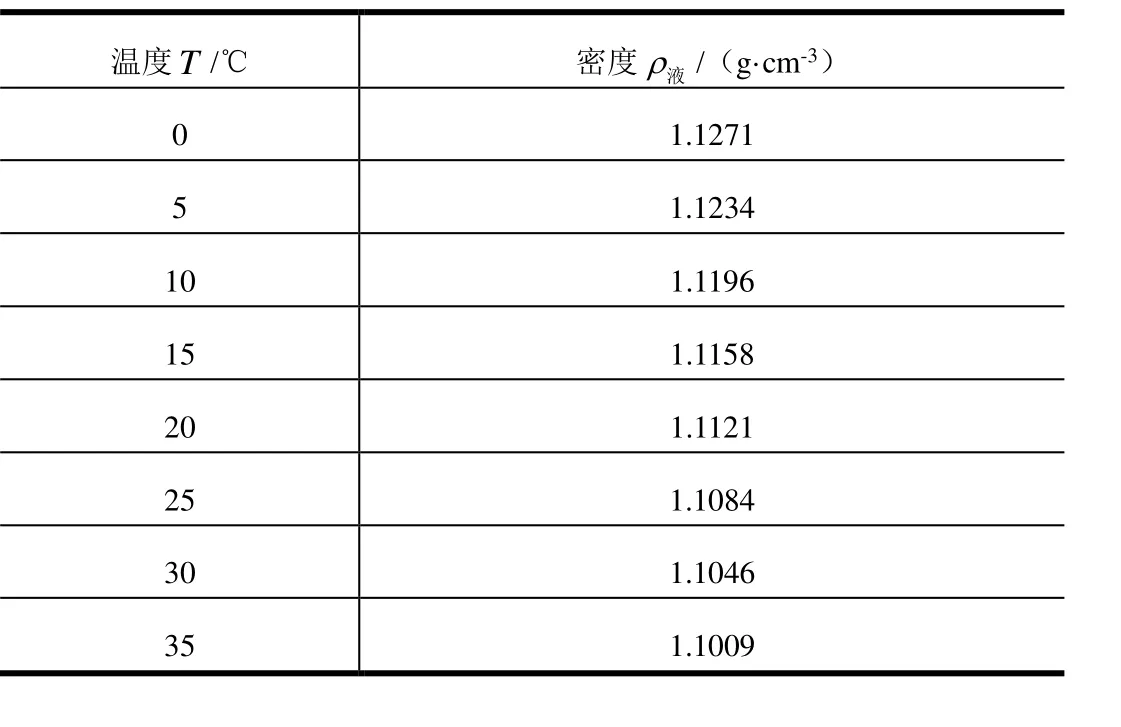
表1 单推-3密度在不同温度下的取值Tab.1 Density Value of DT-3 at Different Temperatures

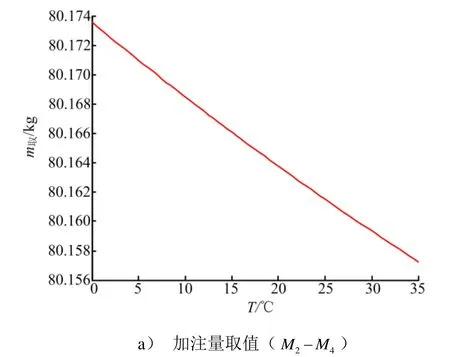
图5 加注量取值与加注控制量随T变化曲线Fig.5 Curve of Filling Quantity and Filling Control Quantity Changing with T
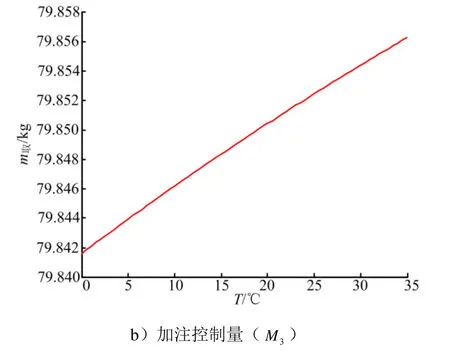
续图5
由此可见,对加注量误差而言,气体压力误差的影响明显大于温度误差的影响。为保证加注量取值的准确性,应尽量减小调压误差、压力表读值误差和贮罐内气枕压力测量误差等。
4 结 论
采用挤压式加注和称重计量的火箭推进剂加注量取值存在一定的方法误差。在分析现有加注量取值方式存在不足的基础上,基于贮罐中气液等体积替换假设,推出了实际加注量和目标加注量时的加注控制量的计算公式。根据历史数据进行的计算分析表明,该计算模型和相关假设是正确可行的。另外,由于贮罐压力、温度、大气压、推进剂密度等值是动态变化的,为了更精准地控制加注量,应在有条件的情况下采用更加精确的数字式传感器,通过实时测量、计算,实现加注阀门启停的自动控制。

