三跨简支梁桥上无缝线路纵向力计算分析

张震

摘要：为研究32m跨径简支梁桥轨道以及桥梁纵向受力特性，通过有限元法、梁轨相互作用相关理论，采用线-桥-墩一体化空间有限元模型，以某三跨32m跨径简支梁为例，利用有限元软件ANSYS建立有限元模型，对简支梁桥上无缝线路纵向力，包括伸缩力、挠曲力、制动力及梁轨位移进行计算，分析梁轨之间相互影响的作用及纵向力变化的规律。

Abstract： In order to study the longitudinal force characteristics of the 32m span simply supported beam bridge and the bridge， the finite element method and the theory of beam-rail interaction are used to adopt the line-bridge-dock integrated space finite element model to simplify the three-span 32m span. Taking the beam as an example， the finite element model is established by the finite element software ANSYS. The longitudinal force of the seamless line on the simply supported beam bridge， including the telescopic force， the flexing force， the braking force and the beam-rail displacement， is calculated.Analyze the interaction between the beam and the track and the law of the longitudinal force change.

关键词：简支梁桥;桥上无缝线路;梁轨相互作用;ANSYS

Key words： simply supported bridge;CWR on bridge;girder rail interaction;ANSYS

中图分类号：U213.9                                       文献标识码：A                                  文章编号：1006-4311（2019）29-0197-03

0  引言

桥上无缝线路主要研究线路与桥梁的纵向相互作用机理及轨道、桥梁的结构设计，保证轨道及桥梁结构在温度、列车荷载作用下满足强度和稳定性的要求[1]。本文以某高速铁路三跨简支梁为例，利用有限元软件对其进行计算分析，分析了列车荷载、制动力、伸缩力对梁轨系统的影响，为高速铁路桥梁铺设无缝线路的设计提供参考依据。

1  计算原理及方法

1.1 梁轨相互作用原理  由于温度的变化或列车荷载的作用，桥梁与钢轨之间产生相对位移[2]。梁轨相互作用原理，是求得钢轨纵向力与位移分布、墩台受力和墩顶位移的关键，从而进行桥上无缝线路结构设计的依据[3]。

1.2 计算方法  桥上无缝线路纵向力包括伸缩力、挠曲力、制动力和断轨力[4]。本文利用有限元软件ANSYS进行有限元建模，对桥上无缝线路进行计算分析。利用ANSYS软件中Beam188单元模拟桥梁，用非线性弹簧单元模拟道床纵向阻力和扣件，全桥共3跨，每跨32m，按实际钢轨间距0.5m划分单元。

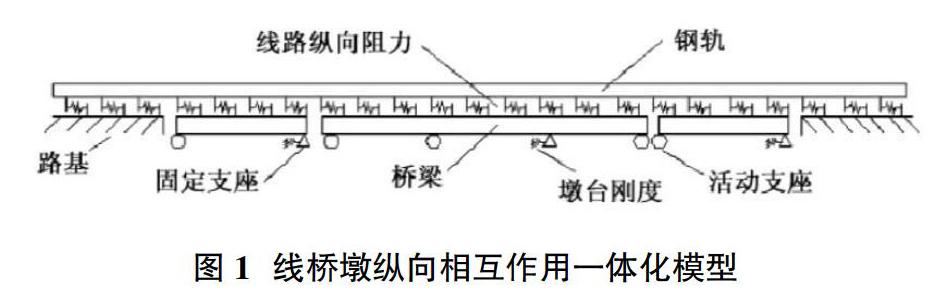
1.3 计算模型  桥上无缝线路纵向力分析可以采用图1所示的线-桥-墩一体化的有限元模型进行计算。该模型将扣件及道床阻力特征采用非线性弹簧单元，桥梁下部纵向刚度采用线形弹簧单元[5]。在建立三跨32m跨径简支箱梁计算模型时，为了消除边界条件对于简支梁桥上无缝线路纵向力和位移计算的影响，考虑该简支梁桥两端路基100m范围以内的钢轨及扣件。

1.4 模型计算基本假设  ①伸缩力、挠曲力、制动力分开计算，不考虑相互叠加时的影响。②计算伸缩附加力时，根据规范，本文取混凝土桥梁升温为15摄氏度。③桥梁墩台纵向水平刚度假定为线形，计算时不考虑固定支座纵向刚度的影响[6]。

2  模型计算分析

2.1 计算参数  本文以3跨32m简支梁为例，支座采用“固定-活动-固定-活动”形式布置，固定支座全部设置在梁的左端，活动支座全部设置在梁的右端，建立空间结构模型对其进行纵向力计算分析。

我国无缝线路普遍采用的钢轨类型为CHN60型，其基本参数见表1。

我国铁路桥梁常用32m跨径简支箱梁桥，本文以3跨32m简支梁箱梁作为研究对象，梁体参数见表2。

根据《暂规》，跨度32m和40m梁的墩台纵向水平线刚度最小限值为400kN/cm和700kN/cm。考虑上述因素，本文墩台刚度取值见表3。

2.2 伸缩力计算结果  钢轨伸缩力计算时，混凝土有砟桥梁温度变化为15℃。钢軌纵向位移如图2所示，梁轨相对位移如图4所示，伸缩力结果如图5所示。

由计算结果可知，钢轨伸缩位移在桥梁中部最大，最大值为2.12mm，最大梁轨相对位移为3.9mm，钢轨伸缩附加力在桥梁两端桥台处较大，在桥梁中部较小，最大值为108kN。

2.3 挠曲力计算结果  列车通过桥梁时，梁体发生挠曲变形。通过本文的计算可以得到，钢轨最大挠曲力为202kN，钢轨最大纵向位移为2.68mm，梁轨相对位移最大为4.5mm。

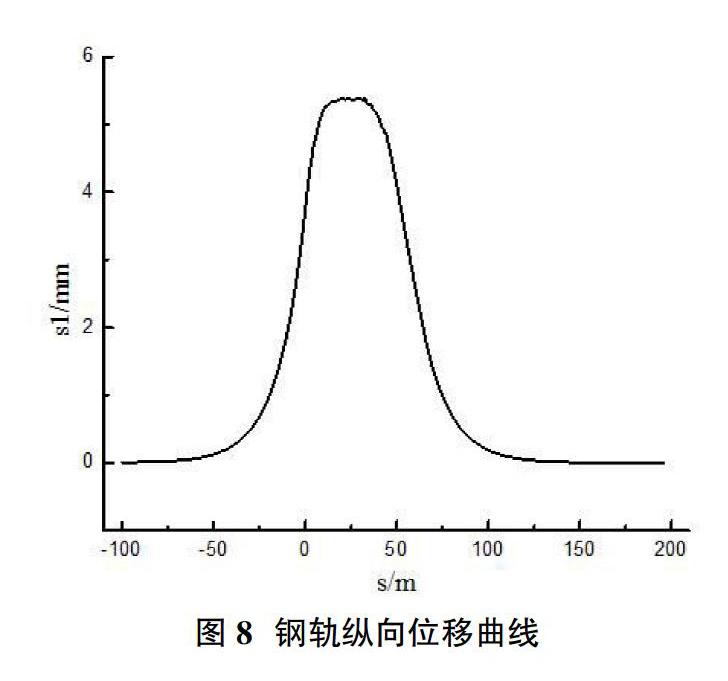
2.4 制动力计算结果   列车在桥上制动时，钢轨顶面将产生制动作用力，从而使梁和钢轨轨产生相对位移，形成梁轨纵向作用力相互影响系统。本文计算制动力时，分为右入桥和左入桥两种形式，结果如图9、图10，钢轨最大位移为5.38mm，发生在桥梁中部位置，右入桥形式下钢轨最大制动力为163.5kN，最大制动力出现在二号桥墩，左入桥形式下最大制动力为162.6kN，发生在一号桥墩。

3  结论

以某高速铁路3跨32m简支梁为例，使用ANSYS建立模型计算桥上无缝线路纵向力，包括伸缩力、制动力、挠曲力，得到了高速铁路3跨32m简支梁桥上无缝线路纵向力，以及梁轨相对位移的变化规律。①钢轨的伸缩附加力最大值发生在0号桥台处，温度荷载作用下，桥跨体系两端的伸缩力较大，越往中间跨，伸缩力越小。②三跨简支梁桥中，桥台刚度对第一跨支座力、以及设固定支座一端桥台的钢轨受到的纵向力影响较大，对其它各跨支座、以及设活动支座的另一侧桥台附近的纵向力影响较小。③制动力的最大值较大，所以，制動荷载是影响纵向力大小的一个重要因素。

参考文献：

[1]王平.高速铁路桥上无缝线路技术[M].北京：中国铁道出版社，2016.

[2]广钟岩，高慧安.铁路无缝线路[M].北京：中国铁道出版社， 2005.

[3]黎国清.高速铁路桥上无缝线路附加力研究[J].中国铁道科学，1997，18（3）：15-23.

[4]TB10015-2012，铁路无缝线路设计规范[S].

[5]高应安.连续梁桥无缝线路计算分析[J].铁道建筑，2005（11）：18-20.

[6]余江.高速铁路桥上无缝线路纵向附加力分析研究[D].北京：北京交通大学，2008.

[7]马骏.56m大跨度简支梁结构分析[J].价值工程，2018，37（24）：120-122.