江西省万元工业增加值用水量预测和可达性及影响因子分析

曾 智，刘春成，王开拓 ，付艳杰

(1 江西省水利规划设计研究院，江西 南昌 330029；2 中国农业科学院农田灌溉研究所，河南 新乡 453002； 3 青海民族大学，青海 西宁 810007)

水资源是社会经济发展的基础资源之一，从中国发展历史过程来看，水资源开发利用模式已经逐渐从粗放的高耗水高污染模式向节水优先可持续发展的模式转变[1]，从2011年中央1号文件和中央水利工作会议明确要求实行最严格水资源管理制度，确立水资源开发利用控制、用水效率控制和水功能区限制纳污“三条红线”[2]，从制度上推动了经济社会发展与水资源水环境承载能力相适应。从宏观角度看，中国各行业水资源用水效率相对不高，仍普遍存在高耗水、高污染和循环利用率低的问题，水效提升空间巨大[3]。《工业绿色发展规划(2016—2020年)》指出，2020年中国单位工业增加值用水量将在2015年基础上下降23%，作为“十三五”期间工业绿色发展的主要指标[4]。

万元工业增加值用水量作为工业用水考核的重要指标，具有非常重要的地位，越来越受到人们的关注。为此，本文以江西省11地市2010—2016年万元工业增加值用水量为主要研究对象，分析其变化趋势并预测2020年和2030年万元工业增加值用水量，预判2020年的万元工业增加值用水量的可达性，为江西省未来一定时期内“三条红线”用水效率控制指标的制定提供一定的参考。

1 预测分析方法

万元工业增加值用水量是指每增加万元的工业增加值所取用的水量，是工业用水量与万元工业增加值的比值[5]。本文通过多种函数模型、年均递减率模型和弹性模型等拟合江西省11地市万元工业增加值用水量2010—2016年的变化趋势，并预测2020年和2030年万元工业增加值用水量指标。

函数模型的主要解决途径是寻找一条较为简单、平滑的曲线，构造一个连续函数近似表达万元工业增加值用水量的历年变化趋势；递减率模型是基于万元工业增加值用水量呈现一般逐年递减变化趋势而言，即整体上的递减趋势可用年平均递减率来预测；弹性系数法是在对一个因素发展变化预测的基础上，通过弹性系数对另一个因素的发展变化做出预测的一种间接预测方法[5]，各模型表达式如下[6-8]：

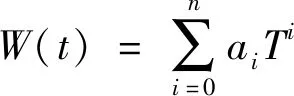
(1)

指数函数：W(t)=CeBt

(2)

幂函数：W(t)=CtB

(3)

对数函数：W(t)=Clnt+B

(4)

Logistic函数：W(t)=A/(1+B+exp(-Ct))

(5)

递减率模型：W(t)=W0×(1-δ)t′

(6)

弹性系数模型：W(t)=

(7)

式中Wi——i年万元工业增加值用水量；t——时间；W0——基准年值；W(t)——当年值(含预测年份)；G(t)——当年万元工业增加值；G0——起始年万元工业增加值；ai、A、B、C——常数项，n——多项式最高次阶数；t′——预测年份与起始年份间隔年数；k——工业用水量年均增长率与工业增加值年均增长率比值；M0——起始年工业用水量；δ——万元工业增加值用水量年均下降率。

2 三大信息准则

在选取最优模型时，应用Root Mean Square Error(RMSE)、Akaike Information Criterial(AIC)和Bayesian Information Criterial(BIC)准则对各模型拟合效果进行比较，三大信息准则具体表达式为：

(8)

(9)

(10)

RMSE准则法是以均方根误差最小为最优函数。AIC信息准则包括2个部分：函数拟合偏差与函数参数个数导致的不稳定性，n为样本数，m为模型参数个数，判断依据是AIC数值越小则说明拟合度越好；BIC信息准则的判别方式与AIC信息准则一致，同样是数值越小，模型拟合度越高。

3 主成分分析法

主成分分析也称主分量分析，旨在利用降维思想，把多指标转化为少数几个综合指标(即主成分)，其中每个主成分都能够反映原始变量的大部分信息，且所含信息互不重复[11-12]。这种方法在引进多方面变量的同时将复杂因素归结为几个主成分，使问题简单化，同时得到科学有效的数据信息。

假设用p个变量来描述研究对象，分别用X1,X2,……,Xp来表示，这p个变量构成的p纬随机向量为X=(X1,X2,……,Xpt)。设随机向量X的均值为μ，协方差矩阵为∑。对X进行线性变化，考虑原始变量的线性组合：

(11)

主成分是不相关的线性组合Z1,Z2，……,Zp，并且Z1是X1,X2,……,Xp的线性组合中方差最大者，Z2是与Z1不相关的线性组合中方差最大者,……,Zp是与Z1，Z2,……，Zp-1都不相关的线性组合中方差最大者。Z1,Z2,……,Ze(e≤p)为构造的新变量指标，即原变量指标的第一、第二、……、第e个主成分。

4 实例应用

4.1 万元工业增加值用水量趋势及预测分析

本文以江西省11个地市2010—2016年统计年鉴公布的万元工业增加值和水资源公报各行政区万元工业增加值用水量为基础，结合江西省第3次水资源调查结果(表1)，将历年万元工业增加值转换成2010年可比价，采用前述各函数模型，利用SPSS和MATLAB等软件进行曲线拟合(表2、图1)，各模型均能较好地反映各地市万元工业增加值用水量的年际变化趋势。其中，指数或Logistic函数模型拟合值的信息准则判别结果最小，相应的残差累计最大值为0.018 5，最小值为0.000 4，表明拟合效果最佳，其次拟合效果较好的为递减率模型和弹性系数模型。

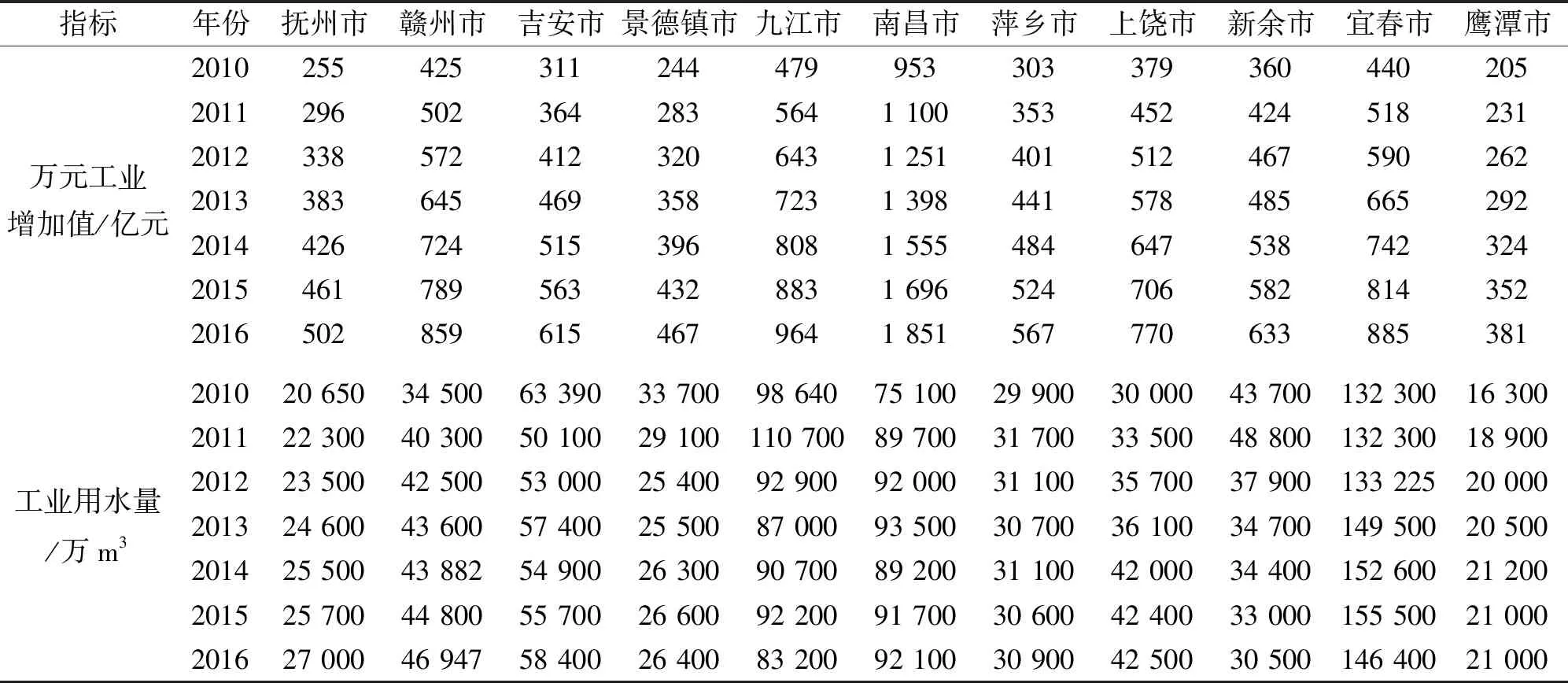
表1 江西省万元工业增加值及其用水量

注：万元工业增加值是相对2010年的可比价

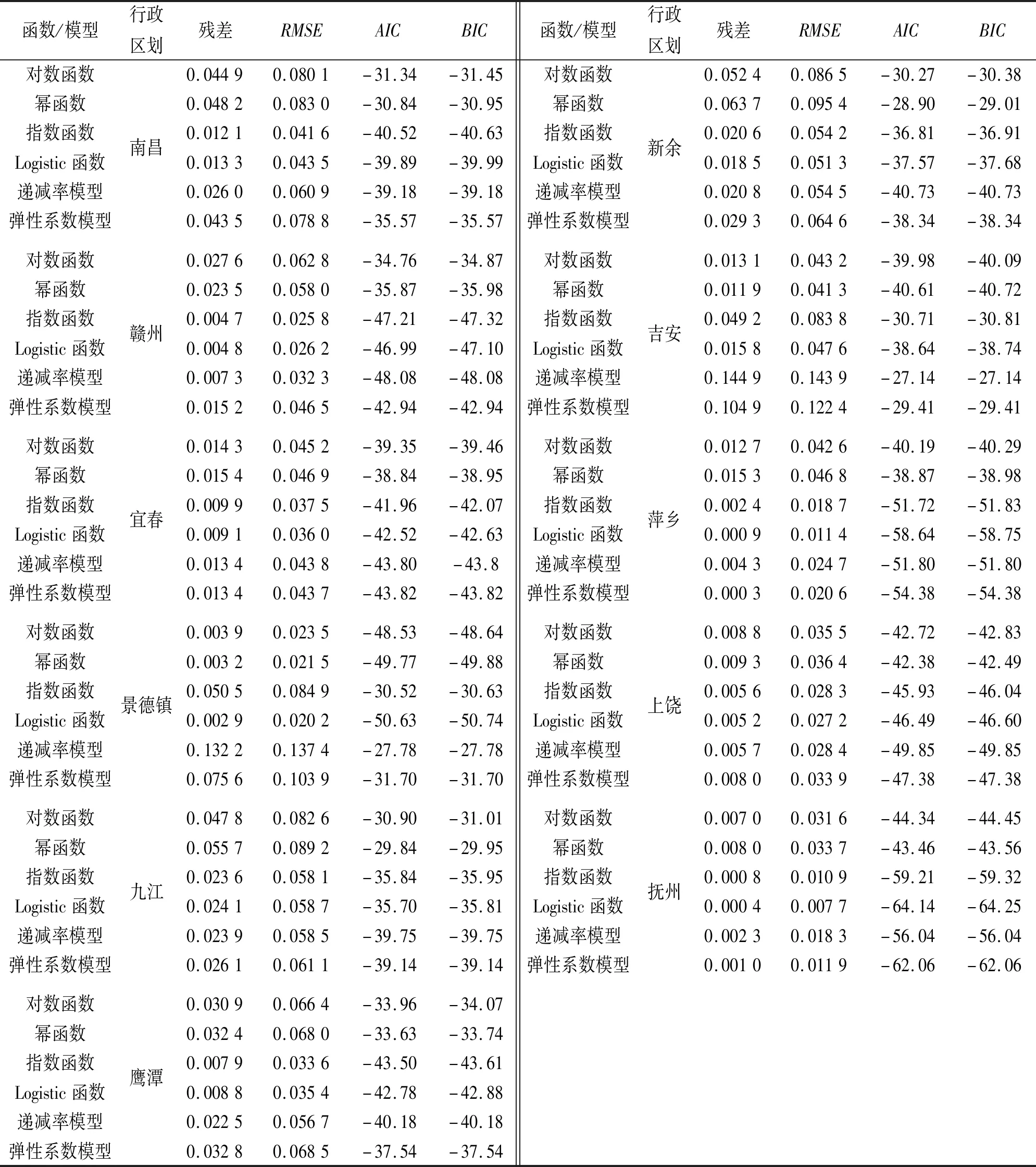
表2 江西省各地市万元工业增加值用水量变化趋势拟合效果

注：考虑到多项式的物理意义不够明确，本表未将多项式拟合成果作为比选方案。除弹性系数模型外，均采用万元工业增加值用水量对数值为计算值

本文选取赣西地区工业相对发达的新余市、宜春市、萍乡市和省会南昌市作为典型，绘制了万元工业增加值用水量拟合效果图(实际点据和拟合曲线)，结果见图1。从图1可以看出，各地市2010—2016年万元工业增加值用水量的递减速率相对较快，且往往出现不均匀变化状态。因此，尽管递减率和弹性系数模型具有较强的物理意义，往往拟合效果不如数学函数模型显著；从预测的2020—2030年万元工业增加值用水量趋势分析，年均递减率相对2010—2016年较缓，从某种程度上说明，随着社会经济发展万元工业增加值用水量的降低幅度将逐渐趋于平稳；在不考虑其他因素影响的条件下，若将预测趋势线延长至2040年，则更为显著地体现出万元工业增加值用水量年际递减的变化趋势，恰恰与中国宏观经济现行政策一致，即社会经济将从高速发展向中高速发展转变。

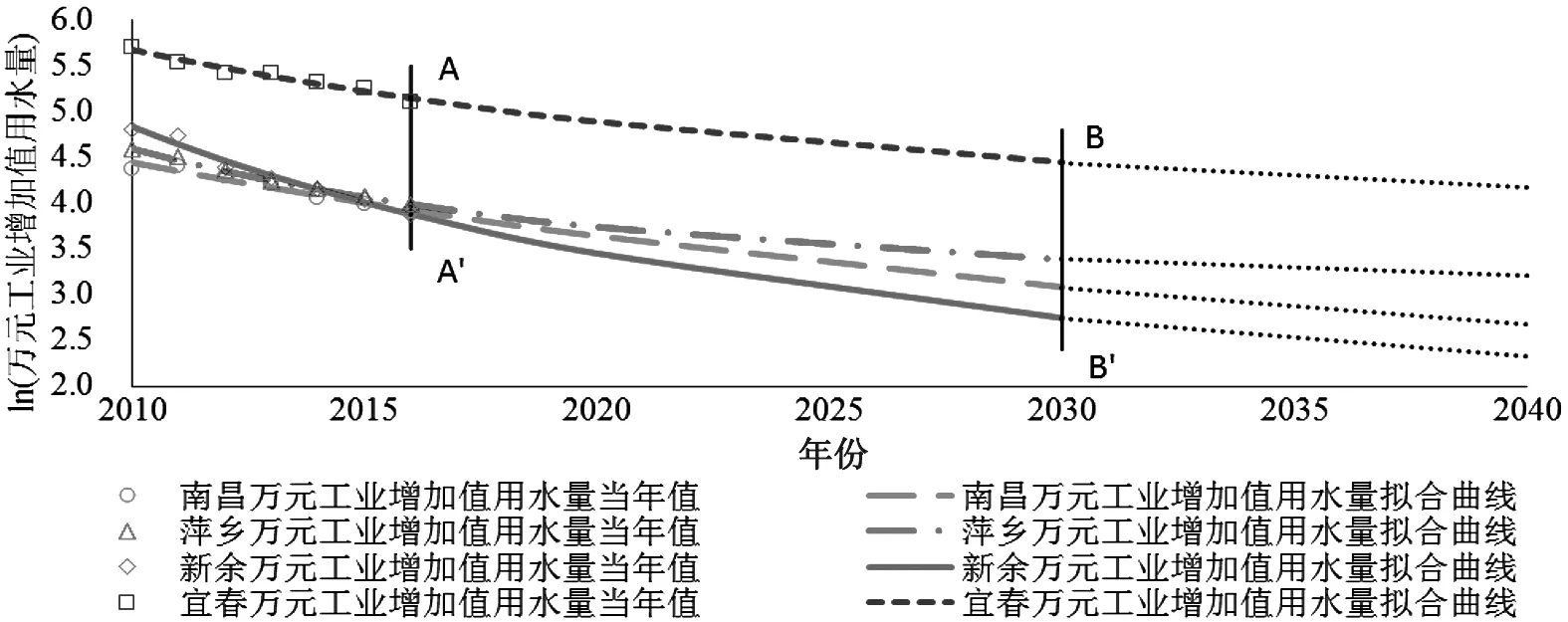
图1 南昌市和赣西地区万元工业增加值用水量拟合效果(Logistic函数模型)

4.2 指标可达性和影响分析

赣水资源字〔2016〕17号对江西省2020年用水效率控制指标给出了明确说明，要求2020年万元工业增加值用水量比2015年万元工业增加值用水量降低30%～35%(全省均值为33%)[9]。通过前述的最优模型(指数或Logistic函数，不同地市有所差异)预测江西省各地市2020年万元工业增加值用水量，并与文件中公布的“三条红线”控制指标[9]比对分析，认为江西省2020年万元工业增加值用水量指标可达标率[7]为81.8%(表3)。

万元工业增加值用水量是一个综合指标，其影响因素多、涉及面广。本文参考相关研究[7,10]选取火电用水占工业用水比(M1)、工业用水占总用水量比(M2)、人均工业用水量(M3)、人均GDP(M4)、工业增加值占GDP比值(M5)、工业增加值增长率(M6)和工业用水量增长率(M7)等7个指标作为万元工业增加值用水量影响因子，通过主成分分析法[13-16]，剖析万元工业增加值用水量影响因子的内在主成分，结果见表4。

从表4可看出，上述因素与江西省各地市万元工业增加值用水量具有较强的正负相关性，影响效力显著。以吉安、景德镇为例，根据累积贡献率大于85%，特征值大于1的准则，吉安市取2个主成分为宜，景德镇取1个主成分为宜，第一主成分为万元工业增加值属性，第二主成分为产业结构与工艺。吉安市第一主成分在火电用水占工业用水比(M1)、工业用水占总用水量比(M2)、人均工业用水量(M3)、人均GDP(M4)、工业增加值占GDP比值(M5)、工业增加值增长率(M6)和工业用水量增长率(M7)等荷载系数的绝对值较大，这些指标分别反映了吉安市工业用水结构和工业增加值等方面的综合实力。其中，工业用水占总用水量比(M2)荷载最大，为0.971，是影响吉安市万元工业增加值的主要因素。也就是说，工业用水量的比重已经成为吉安市万元工业增加值的一个重要因素。此外，火电用水占工业用水比(M1)和工业增加值增长率(M6)荷载系数为负值，说明用水结构没有优化，依然是传统用水模式，火力发电用水量较大，单位产值较低。第二主成分荷载系数较大的是火电用水占工业用水比(M1)和工业用水量增长率(M7)，这些指标反映了吉安市在火力发电和工业用水增长方面的情况。综上，火电循环用水节水改造将作为吉安市降低万元工业增加值用水量的一个非常重要的措施，须花大力气实施循环式用水替代直流式用水模式。

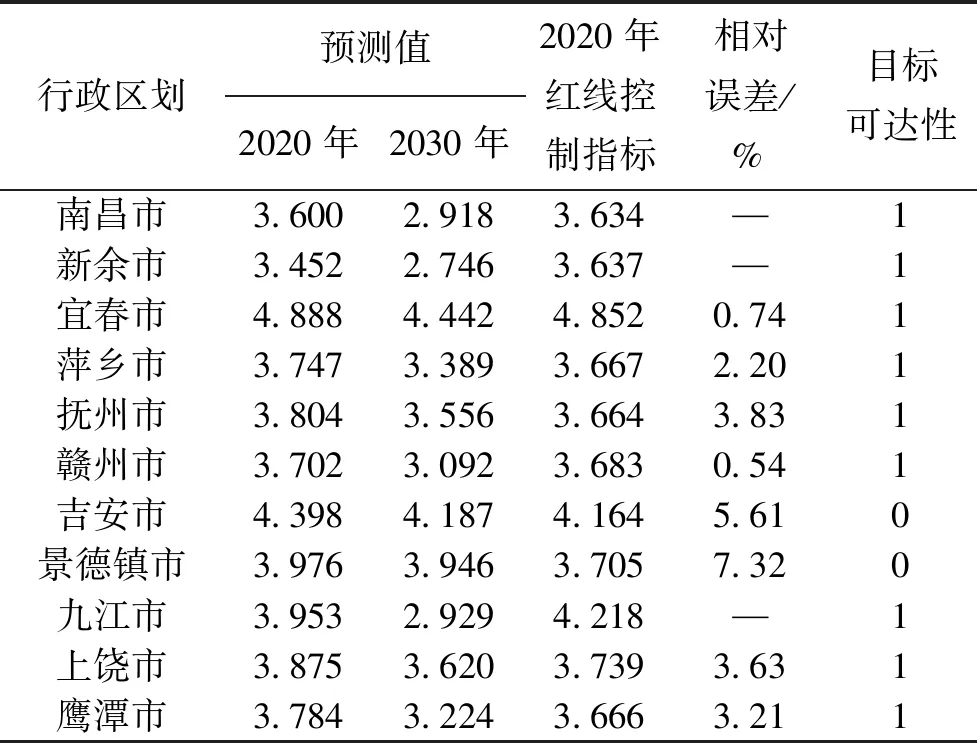
表3 江西省各市预测和控制指标可达性

注：上述指标计算值为ln(万元工业增加值用水量)，考虑到模型拟合误差及对数转换后数值的精度等因素。另外，基于地区社会经济发展不确定性及公布的“三条红线”控制指标的计算基础为当年价，与本文基于可比价存在一定差异性，本文将预测值与指标相差百分比5.0% 以内的地市均认为达标。1表示是，0表示否

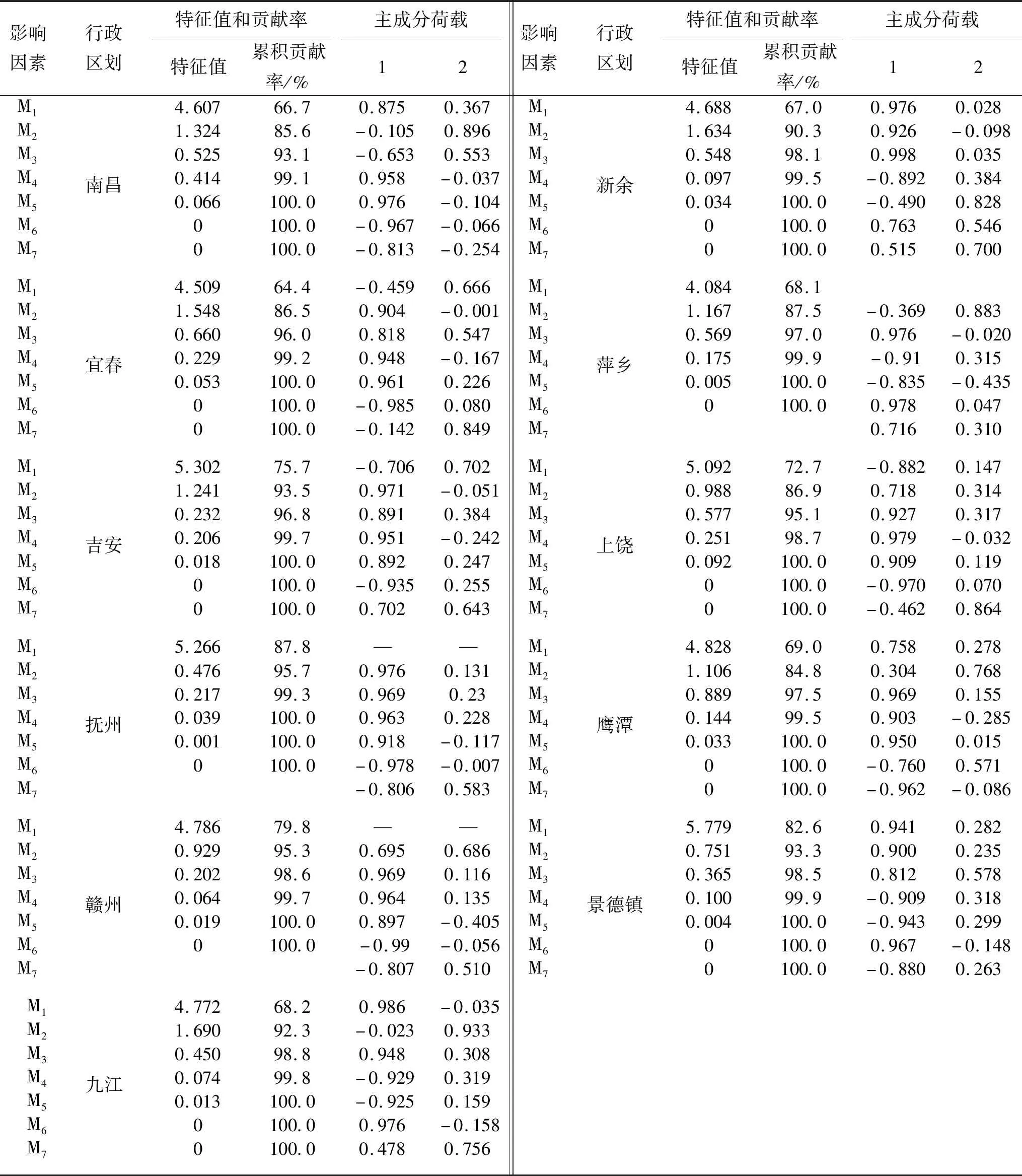
表4 江西省各地级市万元工业增加值影响因子主成分分析结果

注：火电用水量年均不足1 000万m3的地市，不考虑火电用水占比影响因子，主要为抚州、萍乡和赣州市

景德镇第一主成分在火电用水占工业用水比(M1)、工业用水占总用水量比(M2)、人均工业用水量(M3)、人均GDP(M4)、工业增加值占GDP比值(M5)、工业增加值增长率(M6)和工业用水量增长率(M7)等荷载系数的绝对值较大，这些指标分别反映了景德镇市工业用水结构和工业增加值等方面的综合实力，其中工业增加值增长率(M6)荷载最大，为0.967，是影响景德镇市万元工业增加值的主要因素，工业产值的增长幅度已经成为景德镇市万元工业增加值的一个重要因素；人均GDP(M4)、工业增加值占GDP比值(M5)和工业用水量增长率(M7)荷载系数为负值，说明由于人口基数逐年增大，GDP增幅不大，是人均GDP整体下滑，此外随着最严格水资源制度的实施，要求在提高万元工业增加值的前提下，控制工业用水总量。第二主成分荷载系数均不高，相对较大的是人均工业用水量(M3)，为0.578，在一定程度上反映了人均资源占有量对工业增加值的影响。综上，景德镇应以调整产业结构、加大城市品牌效益、强化旅游业发展为突破口。

5 结论

a) 递减率和弹性系数模型具有较强的物理意义，但在社会经济处于上升阶段，往往拟合效果不如数学函数模型显著，即江西省各地市万元工业增加值用水量大都服从Logistic函数或指数函数。

b) 本文预测了2020年和2030年江西省各地市万元工业增加值用水量对数值分别控制在3.452～4.888和2.746～4.442，可为江西省未来一定时期用水效率指标的确定提供一定参考价值。

c) 在不考虑本文所述相关影响条件下，“十三五”末期江西省万元工业增加值用水量达标率为81.8%，与红线控制指标存在一定差异，表明地方须加强水量控制性管理。

d) 火电用水占工业用水比(M1)、工业用水占总用水量比(M2)、人均工业用水量(M3)、人均GDP(M4)、工业增加值占GDP比值(M5)、工业增加值增长率(M6)和工业用水量增长率(M7)等7大因素在第一主成分中与江西省各地市万元工业增加值用水量具有较强的正负相关性，影响效力显著。

e) 万元工业增加值用水量的影响因素在江西省各地市的主成分分析中的荷载有所不同，将第一主成分划定为万元工业增加值属性，第二主成分为产业结构与工艺。以景德镇市和景德镇市为例，前者集中体现为着重火电循环用水改造以寻求单位工业用水产出值增加为降低整体万元工业增加值用水量的有效途径；后者则以近年来城市旅游等第三产业的大力支持和发展为驱动力，调整产业结构，以加大城市品牌效益、做大做强旅游业为突破口。

f) 基于2010—2016年的万元工业增加值用水量系列率定参数从而确定模型，为了提高模型精确度和适应性，后期可采取迭代方式，不断修正模型参数，从而更为精确地反映万元工业增加值用水量变化趋势，预测规划水平年用水量。