一种变步长的微动目标参数高精度提取方法

(空军预警学院, 湖北武汉 430019)

0 引言

目标中存在旋转、振动、进动和章动等微动形式时，雷达回波将产生除目标刚体部分引起的多普勒频率外的附加频率调制，即微多普勒效应(Micro-Doppler Effect)[1]。自2000年 Chen提出微多普勒概念以来，对微动目标微多普勒现象的研究迅速发展起来，其中，旋翼旋转作为典型的微动形式，旋翼微动信息中包含着旋翼的转速和尺寸等信息，利用旋翼转速和尺寸可以对直升机一类目标进行识别，因此受到国内外学者的广泛研究[2-7]。当前窄带雷达对旋翼转速估计的主要方法有时频分析方法[8]、正交匹配追踪算法[8]、Hough变换法[8]、高阶矩函数分析法[9-10]、函数构建法[11]和自相关法[12]。其中，正交匹配追踪算法、高阶矩函数分析法需要用到回波的相位信息；Hough变换计算量大，无法快速进行转速估计；函数构建法虽然计算量较小，但是在旋翼散射点均匀分布时会失效；自相关法必须在叶片个数已知的情况下才能准确估计旋翼转速，并且对于形状规则的直升机旋翼转速估计时，真实转速与估计转速存在着整数倍误差，该误差倍数等于旋翼对称轴个数。因此，旋翼目标的参数估计方法仍需进一步研究。

针对上述问题，本文提出了一种变步长的微动目标参数高精度提取方法，首先建立了旋翼目标的散射点模型，然后通过Gabor变换以及时频图骨架提取估计出旋翼最大瞬时微多普勒频率，接着利用此先验信息，对构建的搜索矩阵进行降维处理，并对转速进行变步长处理，即进行粗搜索和精搜索。然后对搜索矩阵与回波矩阵进行能量积累，可得到积累效果最好的转速值，此时所对应的转速就是估计的最佳转速，随后利用转速估计结果进一步估计出旋翼目标的叶片尺寸。通过本文方法，可以准确估计出旋翼转速和尺寸，并且相对于遍历搜索方法，本文方法明显减少了算法的运算量。

1 旋翼微动目标信号建模分析

基于窄带雷达，在观测时间较短的情况下，旋翼目标不会出现距离单元走动，若观测时间较长，旋翼目标出现距离单元走动现象，此时对旋翼目标进行运动补偿后，旋翼目标的运动状态可等效为悬停状态[13]。为简化分析，假设目标与雷达处于同一个平面，如图1所示，雷达到旋翼目标旋转中心的距离为RC，假设旋翼微动目标为散射点模型，旋翼某一个叶片上的散射点P到旋翼中心的距离为r(0≤r≤l，l为旋翼叶片长度)，P点到雷达的距离为RP，同时P点以角速度ω绕旋转中心C旋转，初始时刻P点的初始旋转角为θ。

图1 旋翼目标模型

设雷达发射信号为窄带线性调频信号[2]：

(1)

旋翼叶片上散射点的回波信号经脉冲压缩后可表示为

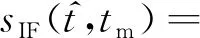
(2)

式中，K为叶片数目，i为旋翼上的第i个叶片，N为目标单个叶片上的散射点数目，j为叶片上的第j个散射点，σij为散射点的散射系数，B为发射线性调频信号带宽，λ为发射信号波长，Rij(tm)为旋翼上散射点到雷达的距离[13]。

Rij(tm)=RC+rijcos(ωtm+θij)

(3)

由式(2)可以看出，旋翼目标微多普勒相位为

(4)

由式(4)可知，散射点的微多普勒呈现余弦函数形式，而余弦函数的周期与旋翼旋转周期是一致的。且不同叶片上散射点引起的微多普勒曲线有着不同的初相，而同一叶片散射点初相是一致的，差异在于多普勒频率峰值大小的不同。对应式(4)，可知旋翼目标瞬时微多普勒频率为

(5)

2 旋翼目标微动特征提取

本文提出的变步长旋翼微动特征提取方法共分3步：第一步是通过Gabor变换和图像骨架[5]提取的方法估计出目标的最大瞬时多普勒频率；第二步是在第一步的基础上通过降维处理以及将搜索过程进行变步长处理，即分为粗搜索和精搜索；第三步是利用能量积累的思想，在时频域对回波数据矩阵与降维后的搜索矩阵进行能量积累，通过积累的效果来估计旋翼目标的转速，最终通过旋翼转速与最大瞬时多普勒频率和旋翼尺寸的严格数学关系来估计旋翼尺寸。

2.1 基于Gabor变换的时频分析及骨架提取方法

由式(2)可以看出，旋翼转动的微多普勒是一个非平稳时变信号，因此需要采用局部分析方法即时频分析来对信号进行处理。由于在窄带雷达中，散射点的微动幅度通常在一个距离分辨单元内，其一维距离像表现为一条平行于方位向的直线，只需要取出该距离门的数据进行时频分析即可。常用的时频分析方法有短时傅里叶变换(Short Time Fourier Transform, STFT)、Wigner-Ville分布(Wigner-Ville Distribution, WVD)、平滑伪WVD (Smoothed Pseudo Wigner-Ville Distribution, SP-WVD)、S方法(S-Method, SM)等[14]。其中，STFT是最常用的基于匹配滤波的时频分析方法，当STFT选取的窗函数为高斯窗时，称之为Gabor变换，根据测不准原理，在所有可能的窗函数中，高斯窗函数能得到最好的时频效果。

对式(2)进行Gabor变换可以得到微动目标信号的时频图，其表达式[9]为

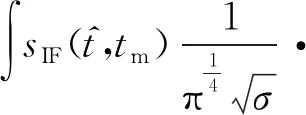
(6)

由式(5)可以看出，在时频图上，旋翼目标的微多普勒曲线是一个三参数的正弦曲线，信号的能量集中在曲线上。图2给出了一个三旋翼目标，且每个旋翼上仅有叶尖处有散射点时的时频特征曲线示意图。

图2 时频特征曲线示意图

由于时频分析受到其分辨率的影响，直接提取参数的误差较大，为了减少后续处理的运算量以及提高参数提取的准确度，从图像域的角度出发，对时频图图像进行阈值处理、平滑处理和二值化处理，而后提取出微动目标正弦曲线的骨架，此时的图像矩阵中只包含“0”和“1”两个值，其中“1”出现的位置即为特征曲线的骨架。这样的骨架同样表征了信号的频率随时间的变化规律，提取骨架的表达式为

(7)

由式(7)可知，此时可以通过时频图骨架准确地找出曲线的极值位置，从而提取出微动目标的最大瞬时微动频率：

(8)

从式(8)可以看出，对于旋翼目标的转速和尺寸参数估计，可以先估计其中一个参数，然后利用严格的数学关系估计出另外一个参数。下面本文提出一种基于该原理的旋翼目标转速和尺寸估计方法。

2.2 基于降维后的变步长微动参数高精度估计方法

目前除了传统的转速估计方法外，还有许多利用微多普勒正弦调制曲线为先验知识的微动参数提取方法，如复经验模式分解(CEMD)、匹配傅里叶变换、扩展Hough变换等，但是上述方法均计算复杂，运算量大。

针对上述问题，本文提出一种降维后的变步长微动参数估计方法，该方法将对微动目标尺寸参数和转速参数的二维联合估计，通过将提取到的微动目标的最大瞬时微动频率作为先验信息，对其转化为分别估计。在估计转速时，首先构建搜索函数：

(9)

为了方便分析，这里假设目标初相θ已知，由分析知道旋翼目标的微多普勒曲线是一条正弦曲线，其表达式可以写为

fm-D=fm-Dmaxsin(ωtm+θ)

(10)

由式(5)、式(10)可知，当r为最外侧散射点时，瞬时微多普勒频率取到最大值，此时

(11)

将搜索函数改写为

(12)

那么搜索矩阵可表示为

(13)

由于构建的搜索矩阵仅利用了一个叶片最外侧散射点的最大瞬时微多普勒频率，因此可以在不知道叶片个数的情况下进行转速的搜索。对HQ×M每行进行Gabor变换，可以得到q个时频数据矩阵V：

V=[V1,V2,…,Vq-1,Vq]

(14)

由于时频分析方法是利用时间变量和频率变量来表征信号的能量分布密度，因此可利用回波信号经时频分析后的数据矩阵J与搜索函数的时频分析矩阵V进行点乘来进行能量的积累，能量积累的效果仅与搜索函数中的ω有关。

F=J·V(q)

(15)

(16)

由分析可知，当搜索函数中搜索步进Δω越小时，搜索结果越精确，但是由于本算法需要对每个转速可能值进行时频分析，会导致运算量急剧增大，因此本文在此前提下对搜索过程进行了粗估计和精估计的处理，即变步长处理，利用粗估计找到转速真实值的大致范围，此时估计精度较差，必须利用精估计对粗估计的转速值附近范围内的转速值进行精搜索，最后得到转速估计值。精搜索的次数越多，其估计的精度越高，但是同时会增加算法的运算量，因此本文在进行粗估计后仅进行两次精估计搜索。

在转速搜索范围[ω1,ω2]内，假设一次Gabor变换的运算量为Nr，设置搜索步进为Δ进行粗搜索，所需的运算量为(ω2-ω1)Nr/Δ，而两次精估计的运算量均为10Nr，故变步长的转速估计方法总运算量为

(17)

如果直接采用遍历式的搜索方法，且要达到相同的估计精度，则需要将搜索步进设置为0.01Δ，此时需要的运算量为

(18)

相对于遍历式的搜索方法，变步长的搜索方法的运算量减少了

(19)

在估计出旋翼目标转速后，通过式(8)、式(16)可以估计出目标的尺寸：

(20)

本文提出的基于Gabor变换的变步长微动目标参数高精度提取方法的处理流程如图3所示。

图3 微动目标参数快速提取方法流程

3 仿真分析

为了更加清晰得到本文方法对微动目标转动频率(frot=ω/2π)和尺寸的提取，仿真选择3个旋翼叶片共10个散射点，模型如图4所示，叶片长度为l=6 m，且本文定义的信噪比为脉压后的信噪比。具体仿真参数如表1所示。

表1 仿真参数

图4 旋翼叶片模型

图5是SNR=5 dB，frot=1.41 Hz时，利用本文方法对旋翼目标转速进行估计的结果；图6是SNR=5 dB，frot=3.14 Hz时，旋翼目标转速的估计结果；图5(a)和图6(a)是旋翼目标回波所在距离单元的Gabor变换时频分析结果；图5(b)和图6(b)是对时频图进行骨架提取的结果；图5(c)和图6(c)是设置搜索步进为0.005 Hz对转速进行遍历搜索的搜索结果；图5(d)和图6(d)是将遍历搜索方法改为变步长搜索方法后，设置搜索步进为0.5 Hz对转速进行粗搜索的搜索结果；图5(e)和图6(e)是在粗搜索得到的最佳搜索结果附近，将搜索步进设置为0.05 Hz对转速进行第一次精搜索的搜索结果；图5(f)和图6(f)是在第一次精搜索的最佳搜索结果附近，将搜索步进设置为0.005 Hz对转速进行第二次精搜索的搜索结果。

在图5(a)和图6(a)中，可以看出此时目标的微动频率是受正弦调制的，利用时频图可以提取出图5(b)和图6(b)中所示的时频图骨架，并且可以利用骨架估计出最大微多普勒瞬时频率。对转速进行遍历搜索时，由于已经将搜索步长设置得足够小，因此在图5(c)和图6(c)中可以看到其搜索精度很高。另一方面，正是由于其搜索步长很小，需要对搜索范围内800个转动频率点进行搜 索，导致遍历搜索过程很慢，因此需要提出一种既能保证搜索精度，又能提高搜索速度的算法，即变步长的搜索方法。将搜索方法改为变步长的搜索方式后，此时仅需要对30个转动频率点进行搜索，搜索量大幅下降。但是在进行粗搜索时，此时转动频率与搜索步进存在失配情况，本文方法只能够估计出目标转动频率的大致范围，估计误差很大，因此还需要通过改变搜索步长对转动频率进行估计，其估计结果逐渐向真实转速逼近，经过第二次精估计后，本文方法能准确地估计出旋翼目标的转动频率，如果旋翼目标的转动频率还存在多位小数的情况，但是本文在准确估计出小数前几位的情况下，其估计误差带来的影响很小。

图5 本文方法对frot=1.41 Hz的估计结果

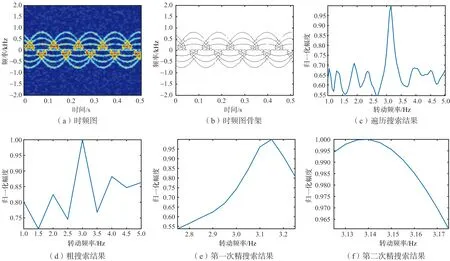
图6 本文方法对frot=3.14 Hz的估计结果

表2给出了本文方法在不同信噪比条件下的转动频率和尺寸估计误差。

通过表2可以发现，本文提出的变步长微动目标参数提取方法对旋翼转速和尺寸的估计精度和对信噪比的适应程度都具有较好的性能。但是在SNR<5 dB时，本文方法的估计误差急剧增大，这是由于此时时频分析方法已经无法得到有效时频图以及相应的骨架，从而无法估计出旋翼目标最大瞬时微多普勒频率，缺失了这一先验信息，本文方法将会失效。

4 结束语

本文提出了一种变步长的微动目标参数高精度提取方法，通过利用旋翼最大瞬时微多普勒频率的先验信息，对构建的搜索矩阵进行降维处理，然后从时频域能量积累的角度出发，对转速进行了粗估计和两次精估计，积累效果最好的转速值即为估计的最佳转速，并通过转速估计值和最大瞬时微多普勒频率估计值估计出旋翼目标的叶片尺寸。通过仿真结果可以看出，本文方法可以较为快速地估计出旋翼转速和尺寸，并且具有很高的估计精度，对信噪比的适应程度也较好。但是，该方法在进行估计时是基于骨架提取结果完成的，在低信噪比条件下该方法的估计精度将急剧下降甚至估计失效，下一步还需要从提高时频分辨率和降噪处理的角度出发，来解决本文方法在低信噪比条件下估计精度不足的缺陷。