基于CFD的散货船船体型线自动优化

赵无忧，郭啸轩，束永昊，常海超

(武汉理工大学 交通学院，湖北 武汉 430063)

0 引言

船型优化在船舶研发设计中始终占据重要位置，国内外很多学者对此展开研究。文献[1-3]主要研究了多目标遗传算法对优化结果的影响并建立了优化平台，进行了海上三体补给运输概念船和双体高速船的优化，获得了较好的优化结果。文献[4]结合稳健设计方法和Monte Carlo试验设计、遗传算法进行了高速双体船初步设计阶段的不确定性优化，并验证了此方法具有一定的工程实用价值。文献[5-7]利用径向基函数插值方法对船型优化进行了深入研究，并自主研发了基于CFD的船型优化平台，采用粒子群算法对Series60 船体曲面进行修改，以产生球鼻艏形状，再对修改后的船型进行艏部和艉部优化，获得了良好的减阻效果。研究表明，利用径向基插值函数方法和粒子群算法集成的平台适合工程需要。

船型优化平台主要由四部分构成，即船型参数化变形模块、静水力计算模块、CFD 计算模块、优化模块。本文重点介绍了基于CFD船型优化平台的模块构成，并基于此平台，完成了对某条隐形球鼻艏散货船的优化并获得了新船型。

1 平台优化框架及过程

船型优化平台主要由四个模块构成，总体框架见图1。

图1 优化过程及原理

进行船体优化时，首先将船体曲面离散成空间点云形式，根据径向插值函数进行船体曲面参数化变形；然后对静水力数据进行约束，通过CFD模块计算静水力数据;最后利用平台集成的粒子群(PSO)优化算法得到船型最优解。

2 船型优化平台模块构成

2.1 基于RBF的船体曲面变形模块

本平台利用径向基插值函数(RBF)，通过修改船体NURBS曲面的空间点云实现了船体曲面的参数化变形，进而生成新的船体曲面。

径向基函数是一类以距离为变量的函数集合，它属于多元函数，通常采用常见的欧几里德距离‖X-Xi‖作为函数变量。各基函数的具体形式为：

Φ(‖X-Xi‖)i=1,2，…，n

(1)

给定一组离散数据的集合{xi,fi}，i=1,2,…，n，使其满足插值条件：

S(Xi)=fii=1,2,…，n

(2)

式中:fi为控制点坐标的变化量。

该问题可以用以下形式的径向基函数插值方程来解决。

(3)

式中：Φ(‖X-Xi‖)函数为径向基函数；λi为权重系数；Xi为已知的样本数据。

根据式(2)、式(3)，将已知样本点代入式中，可以得到关于权重系数Xi的线性方程组。

(4)

式中：Φy(‖X-Xi‖),i=1,2，…,n。

Aλ=F

(5)

如果A非奇异，那么式(5)可写成：

λ=A-1F

(6)

上述插值问题对于任意数据点集{xi,fi}∈Rd⊗R(i=1，2，…n)，当xi=1，2，…，n互不相同时有唯一解的充分必要条件时：对任何两两不同{xi},对称矩阵A是正定的。

上述计算步骤即是利用径向插值函数进行船体曲面参数化变形的基本原理。

2.2 静水力计算模块

优化船舶时，为了保证优化之后得到的新船型满足光顺性、合理性，需要对静水力数据进行约束。本平台采用了一种基于面元法的船舶静水力计算方法，即将船体曲面离散成两维面元，并将对船体的体积分转化为对面元的面积分，以此来计算船型优化问题中的静水力性能数据。

根据式(7)，可以将体积的三维积分转化成对面积的二维积分。再根据问题需要，对P、Q、R取值，得到相应的静水力数据。

(7)

式中：P、Q、R为变量。

船体湿表面Swet与水线Swl面所围成的部分即为船体排水体积V。

静水力数据包括排水体积、浮心纵向位置、湿表面积等，它们的求法如下。

求解排水体积：P=0,Q=y,R=0

(8)

求解浮心纵向位置：P=0，Q=y2/2，R=0

(9)

其他静水力数据求解步骤如上。

2.3 CFD计算模块

计算流体动力学 (Computational Fluid Dynamics CFD)是计算船舶水动力数值的工具。在计算船体运动时的粘性阻力、兴波阻力、模拟压力分布和数据模型时，常常用CFD与SHIPFLOW(一款船舶水动力性能分析软件)相结合，采用粘性理论和势流理论的计算方法。具体流程为：CFD先在计算机上求解描述船舶流体运动的微分方程组，再对船舶的周围流场进行数值模拟，从而对船舶水动力性能做出评估。

SHIPFLOW计算原理如下：计算时将船体周围流场分为三个区域，每个区域应用不同的计算方法。势流区采用高阶面元法，船体前半部分的边界层区域采用动量积分法计算边界层流，船体中后部的湍流区域采用雷诺平均的Navier-Stokes 方程和k-epsilon湍流模型求解。

2.4 优化模块

本平台优化模块是利用粒子群算法。在粒子群算法中，每个粒子都有速度、位置、适应度三个信息。它们共同作用后可以在规定时间内快速、准确地找到最优解。粒子最佳位置与速度利用如下公式进行计算。

(10)

(11)

2.5 各模块的集成及用户界面开发

基于上述模块，开发了船舶水动力性能多学科综合优化平台，软件具有友好的界面，用户只需要在界面中进行相关优化数学模型的简单设置，即可进行船型单性能的优化，也可进行船型水动力性能的多目标综合优化。优化平台的显示界面见图2。

3 基于CFD的船体曲面自动优化方法

本平台优化流程见图3。

(1)利用径向插值函数对初始船型进行参数化变形。

(2)计算优化船的静水力参数，并验证是否满足静水力约束。若满足，进行下一步计算；若不满足，则循环计算修改，直至得到满足要求的新船型。

(3)对满足要求的船型进行水动力计算(SHIPFLOW)，获得新船型的水动力性能指标。

(4)采用粒子群算法(PSO)对船型进行优化。以兴波阻力最小化为目标，反复计算，直到得到满足要求的新船型。

图2 优化平台显示界面

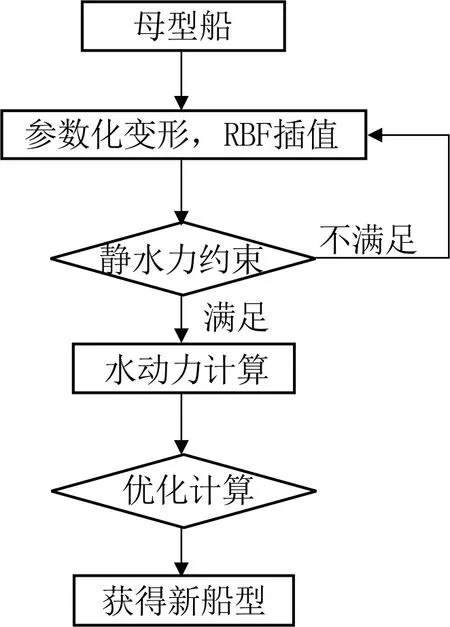
图3 平台优选流程

4 隐形球鼻艏货船水动力性能优化

4.1 优化对象描述

初始船型是一艘隐形球鼻艏散货船，船型见图4，基本参数见表1。

图4 船型(隐形球鼻艏散货船)

表1 船型基本参数

4.2 优化模型的建立

4.2.1 优化目标

以Fr=0.24的兴波阻力Rw最小为优化目标，即minobj=Rws.t.Fr=0.24。

4.2.2 优化变量及范围

船型参数化变换方法决定着优化变量的选取以及变量取值范围的确定，对隐形球鼻艏散货船采用船体曲面非均匀有理B样条(Non Uniform Rational B-Spines，NURBS)表达为基础，通过修改船体型值点坐标来实现船体曲面的参数化变形。

采用径向基插值函数来进行船体曲面参数化变换，需要选取控制点作为控制变量。由于改善船艏形状可以有效减少兴波阻力，因此控制点应选在船艏位置。选取图5中6个点作为设计变量。X1到X6都只在Y方向(船宽)上有改变。

图5 船艏选点位置

设X1至X6在Y方向上的变化量分别为Y1至Y6。优化变量的初始值与变化范围见表2。

表2 变量上下限

4.2.3 约束条件

在进行船型优化时，需要对静水力参数进行数据约束，以保证优化后船体曲面的光顺性。现仅改变船体艏部型线，船长L、船宽B、吃水T、设计水线长Lwl均保持不变，排水体积Δ、浮心纵向位置Lcb在初始船型1%范围内变化。

4.2.4 优化结果及分析

优化算法采用多目标粒子群算法，粒子个数设置为60，权重因子设置为0.8，学习因子为c1=c2=2。通过20 h的优化，得到新的散货船型线。

在约束条件下，优化船的兴波阻力得到有效降低,优化船的排水量和湿表面积增大导致了摩擦阻力增加，从而使总阻力降低偏小。优化前后船型变化见图6、图7。 分析可以发现：优化船型整个艏部有巨大变化；优化后的艏部横剖线呈缓和 U 形，有利于减小兴波阻力；并且优化船产生的球鼻艏下垂，纵剖面呈 S 形，类似于 SV 形球鼻艏，使得船舶在中高速时产生有利的兴波干扰。优化前后数据对比见表3，优化结果见表4。

图6 优化前后纵剖线图对比

图7 优化前后横剖线图对比

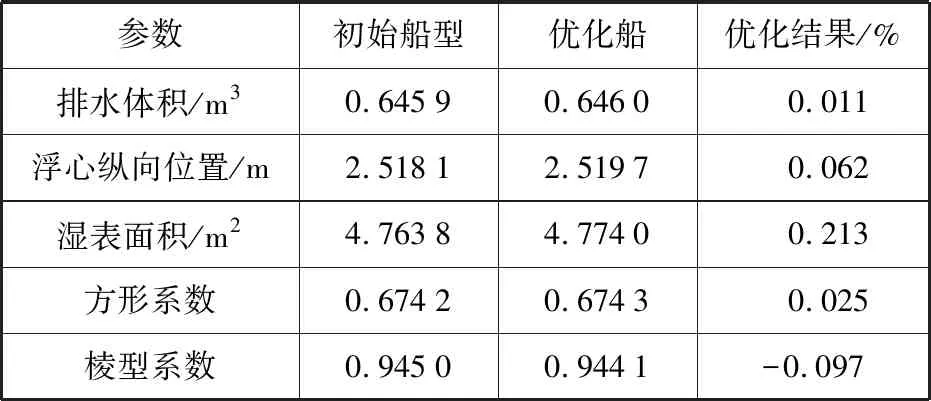
表3 优化前后数据对比

表4 优化结果

优化船兴起的波浪明显比初始船型少，这是因为球鼻艏的兴波与主船体的首横波形成有利干扰，从而使得兴波阻力减小。分析图 8发现，从船艏的第一个波峰开始，兴波幅值都有明显降低，这表明船体掀起波浪的能量减少，船体克服兴波阻力做功减小，兴波阻力得到改善。图9中，优化后在船体中部兴波的波高差减小，兴波阻力有明显降低。

图8 优化前后波形图对比

图9 优化前后舷侧纵切波高图对比

本文以Fr=0.24时兴波阻力最小为优化目标进行优化。优化船的排水量增大了 0.011%，这大大增加了船舶的运载能力，提高了船舶营运的经济性。而湿表面积增加了0.213%，这表明船舶摩擦阻力增加，但由于中高速船摩擦阻力所占比重较小，所以总阻力增加不大。但随着航速提升，兴波阻力成分增加，减阻效果明显得到提升，兴波阻力减阻效果达到10.13%，船舶总阻力减小了3.20%。由此得到了一艘船舶阻力明显减小的新船型。

5 结论

本文以隐形球鼻艏散货船为研究对象，实现了基于CFD的船体曲面自动优化设计。研究工作表明，基于CFD的船体曲面自动优化设计方法具有以下几个特点：

(1)参数化变形模块能够以较少的参数实现船体曲面的变形。

(2)优化模块能够完成优化问题的空间探索，且收敛速度快，优化周期短。

(3)基于面元法的静水力计算方法具有较好的计算精度，满足船型优化设计的需要。

(4)仅需设计人员根据经验布置少量的控制点就可以自动完成船型的优化设计。

(5) 在优化过程中产生大量新船型，极大地拓展了设计空间，适用于船型优化前期阶段探寻最优船型。

(6)开发的船型优化平台，对实现船型的创新设计、提高设计质量、缩短设计周期具有重要意义。