船舶艉部结构特征及对轴系振动影响因素

刘腾龙，刘建朔

（新奥能源控股有限公司，河北廊坊 065001）

0 引言

目前船舶轴系振动引起的船舶艉部结构的振动以及艉部结构特性对轴系反作用问题需要进一步研究。通过对艉部结构特征分析，了解造成轴系振动的重要因素：艉轴架刚度及固有频率、艉部结构刚度及固有频率以及轴系固有频率的大小。建立推进轴系及艉部整体耦合三维有限元模型，分析在不同轴系转速下艉部结构耦合刚度、艉轴架耦合刚度、艉部结构局部振动固有频率以及艉轴架固有频率对轴系振幅的影响，为减小船舶的振动提供一个整体概念的指导意见。

艉部结构的振动研究通常分为三个阶段[1]。第一阶段主要是艉部结构振动的发生是艉部构件与叶频干扰力发生了共振的结果，为了避开叶频激振力影响，将研究方向确定在研究局部构件的固有频率。第二阶段是以Hylarides的研究为起点，指出导致艉部结构剧烈振动的原因是螺旋桨激励过大引起的[2]。第三阶段通过用流固耦合理论来研究艉部振动。但是由于船尾大部分浸入水中，不考虑水介质的耦合虽然使研究变得简单，但是却不符合实际情况[3-9]。

本文将艉部结构有限元模型加以离散化，并列出一系列公式作为艉部结构固有频率计算的理论依据；利用Guyan缩聚法作为艉轴架固有频率计算的理论依据。利用雷诺方程列出求解轴承油膜刚度的计算公式，并且运用小扰动法获得油膜刚度的近似值，利用轴承支承刚度经验公式求解耦合刚度。对轴系振动影响因素的分析。建立推进轴系-艉部结构三维有限元模型，分析艉部结构和艉轴架固有频率、支承刚度对轴系振幅的影响。

1 船舶艉部结构固有频率计算理论

1.1 艉部结构固有频率计算理论

艉部结构的受力十分复杂，因此，在研究艉部结构的振动特征时，需要将艉部结构离散化，建立三维有限元模型。由于艉部结构振动主要是垂向振动，所以本文只研究垂向振动模态。

有限元离散模型的运动方程为

式中：[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{U}为节点位移矢量；{P}为节点载荷矢量。

令式(1)的阻尼和外力为零，并设结构处于以λ为频率的谐振状态，即：

则可由式(1)得广义特征值问题为

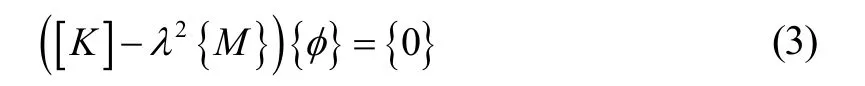
由于船体结构是漂浮在水中的无约束结构，故刚度矩阵是半正定的，为求解特征值问题式(3)，可将其变形为

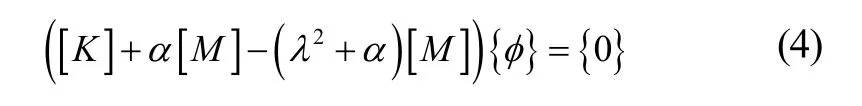
由式(4)求出的振型是精确的，而频率值则可在扣除α(＞0)的影响后得到。

由式(4)求得正则振型和各阶固有频率之后，利用模态变换，由式(1)得主坐标运动方程如下：

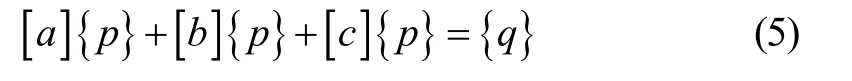
式中：[a]为单位矩阵；[c]为对角阵；[b]在比例阻尼的假定下为对角阵，其对角元素由经验确定；{p}为主坐标；{q}为广义节点力矢量。

由于式(4)表示的是一组解耦的方程，因而很容易求解。

1.2 艉轴架振动特性计算理论

Guyan缩聚法由刚度矩阵的静态凝缩而来。全自由度集静态方程为

式中：[Kff]是刚度矩阵，{xf}为位移向量，{Pff}为载荷向量。

把全自由度集分解为分析子集与删减子集，式(6)变为

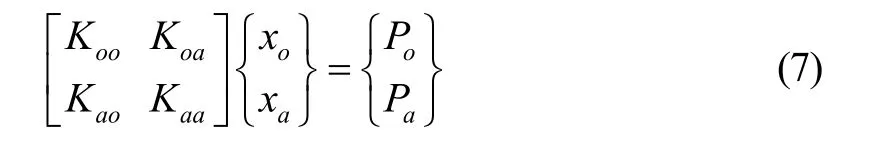
将上式展开可得表达式：

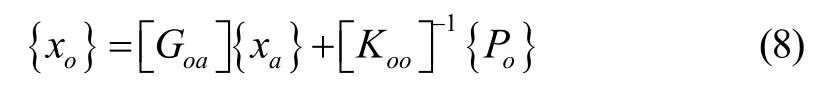
其中，

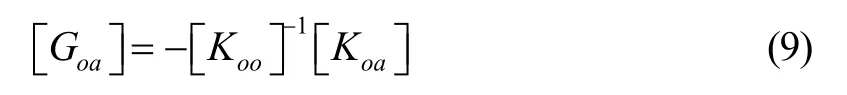
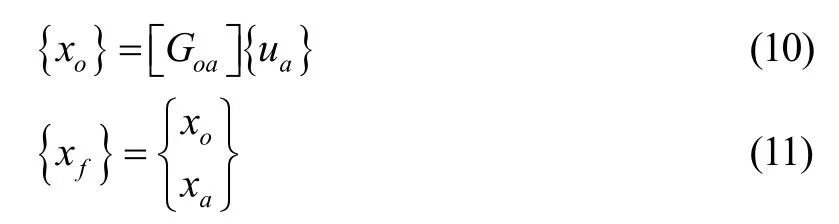
得到{ua}与{uf}的关系为

其中，

式中：[Iaa]为秩为a的单位矩阵。

在式(12)两边同乘[Gfa]T获取分集的凝聚方程为

其中，

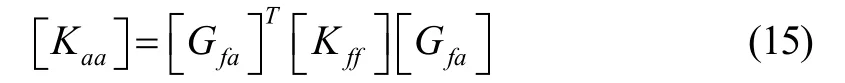
由式解出的即为子集的解。

Guyan缩聚法是用静态凝聚法将[Mff]矩阵减缩，即：

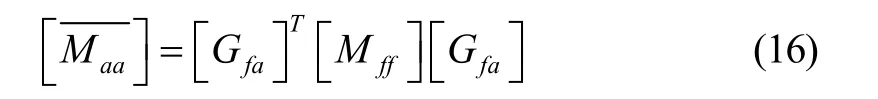
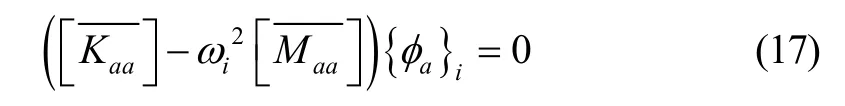
解得ωi为分集的固有频率，{φa}i为相应的振型向量。

1.3 轴系横向振动固有频率计算理论

运用传递矩阵法研究横向振动的固有频率时，需要将轴系以精度为标准分为几个相同的弹性轴段，并且在保证转动惯量和质心都不变的基础上，把每个轴段的质量放在重心处，把各个轴段作圆盘元件处理。同时将联轴节、推进器也当做圆盘处理，它们之间的轴段当做弹性杆处理，并且与实际轴相比，各个轴段刚度不能改变。将轴承当做弹性支座以便求解初始数据，不考虑其他因素，除了离推进器最近的支撑点要取轴承后端 1/3工作长度处以外，其他轴承都把轴承的中心作为支撑点。运用传递矩阵法求解固有频率，过程如下。

1）建立简化模型

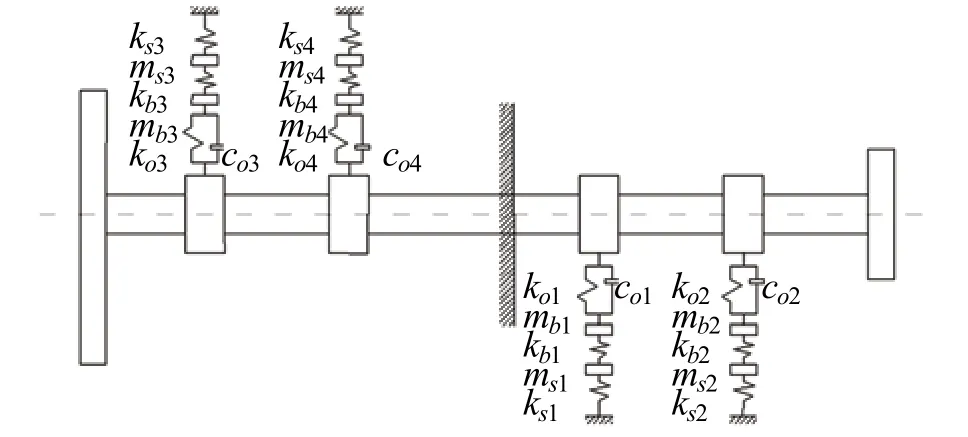
图1 轴系横向振动简化图

2）支、元件和端点编号

轴系是由主支和分支组成的，主支由推进轴系组成，分支数目与轴承数目一样。从艉轴艉管轴承分支为起点进行支的编号，然后按顺序继续编号，最后对主支进行编号。假如根据经验法把一个数据作为分支等效弹簧刚度，那么久不需要分支编号，将整体变为只含主支的单支系统。与此同时从螺旋桨端开始编号。

3）确定求取固有频率的次数

即确定Ω/ω之比(1/j0)。本节只需要获得轴系在进行横振时的固有频率，即Ω/ω=0。

4）给出试算频率值

给出一系列试算频率值Ω0、Ω0+ΔΩ、Ω0+2ΔΩ、Ω0+3ΔΩ...

5）求出支承系统等效刚度

6）计算累积矩阵

累积传递矩阵表示为

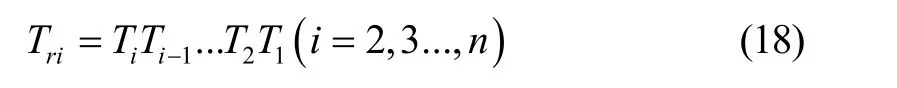
式中：Ti为第i个元件的传递矩阵。于是，主支的传递方程为

螺旋桨是主支的起点，它的左端不受任何拘束。矢量表达式中的弯矩和力的数值相等且恒等于零。假设轴承支承刚度在各个方向都一样，将式(19)进行扩展。

7）观察与主支末端相接的设备种类，根据不同设备确定与之对应的边界条件，最后计算系统剩余量。

如果是刚性铰支连接，系统剩余能量Res为

如果是自由端，系统剩余能量Res为

如果是固定端，系统剩余能量Res为

通过式(21)～式(23)可以对不同边界条件下系统剩余量进行求解。

横向振动固有频率的确定是根据上述公式得出的结论是否等于零或者低于给定的较小值，如果满足上述因素，就将试算频率作为系统固有频率。不然需要重新设定一个试算频率，然后继续操作上述5）、6）、7）过程。图2为系统剩余量Res与试算频率Ω间的关系曲线图，图中曲线以x轴为中心线呈s型分布，它与横坐标的交点ωn1，ωn2，…就是回旋振动的固有频率。

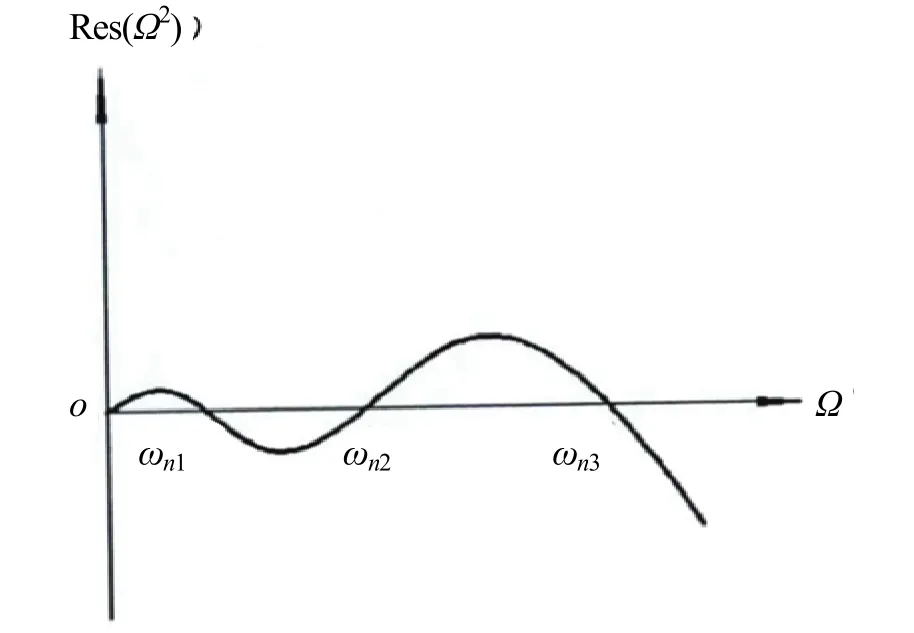
图2 系统剩余量

8）搜索求得固有频率

通过观察上图曲线得知，如果相邻试算频率不同号，两者之间一定有一个固有频率，它能够用插值法得出。

2 艉部结构刚度耦合理论

本部分研究艉部结构与轴承之间支承刚度耦合关系，为接下来研究支承刚度与轴系振动之间的关系提供理论和数据支持。为了更加直观的反映艉部结构与轴承支承系统之间的耦合关系，对该部分做了图3的支承系统简化模型。

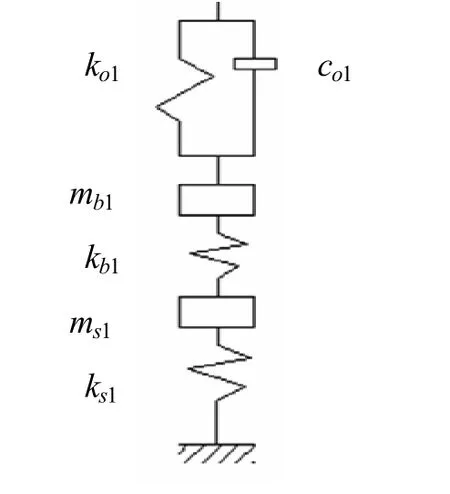
图3 艉部-轴承支承系统简化模型

ko1和co1分别表示油膜刚度和阻尼，ms1和ks1分别表示艉部结构参振系数和艉部结构刚度。在求取耦合刚度时暂时不考虑阻尼、轴承-轴承座之间的关系。

艉部结构刚度可以从整体和局部两方面来考虑。整体刚度计算主要考虑艉部各个部件的分布情况和艉部本身刚度的设计，其中最主要的包括动态刚度、弯曲刚度、扭转刚度；局部刚度计算主要考虑艉部与轴承之间的耦合部位以及两者耦合部位的位置刚度，它的刚度变化取决于艉部加强构件的采用以及耦合处的断面形状等。

重点分析轴承支撑处艉部结构的局部刚度，因此将轴承支撑处艉部双层底刚度作为计算刚度，使用某船舶的实际参数来分析耦合刚度，具体参数如下：双层底底板板厚为8 mm，旁桁材厚度t=6 mm，间距b=2 400 mm，纵骨宽度为0.6 mm，艉部结构局部刚度为1.224×109N/m。

轴承支撑刚度经验公式为

式中：ke为支承系统等效刚度；ks为船体刚度；kb0为油膜和轴承等效刚度。

将艉部结构局部刚度以及上一节中计算出的油膜刚度放进经验公式求解，可以得到艉部结构和轴承支承耦合刚度。

3 艉部结构特征对轴系振动的影响因素探究

3.1 建立有限元模型

推进轴系为细长结构，采用梁单元BAR模拟，梁截面与实际推进轴系截面保持一致。螺旋桨等效为集中质量单元。艉轴架有限元离散概况见表1。

表1 艉轴架有限元离散模型概况

推进轴系（带尾轴架）有限元模型见图4。

图4 艉轴架有限元模型

艉部采用三维结构一艉部梁的杂交模型，按照实际结构建模，相接处使用MPC单元连接。艉部梁采用梁单元BAR模拟，并通过调节截面形状、材料属性，使得有限元模型中各站重量、各截面垂向、横向惯性矩与实船参数基本一致。单元的选取原则为：板型结构采用QUAD与TRI单元模拟，厚度按照各板实际尺寸定义；梁型结构采用梁单元BAR模拟，梁单元截面形状与实际结构一致；实体结构采用实体HEX单元，艉轴架用实体单元建模；质点采用集中质量单元POINT，保证各站重量与实船一致。

有限元模型如图5所示。

图5 艉部结构剖面图

3.2 艉部结构固有频率分析

由艉部结构局部振动的固有频率计算可知该船艉部结构第一及第二阶固有频率分别为1.45、12.1。为了探究艉部结构与轴系耦合系统共振频率以及幅值随转速变化的规律，将结果分为考虑艉部结构和不考虑艉部结构进行分析。具体情况见图 6。从不考虑艉部结构因素的特性图中可以得出一个结论：随着转速的增加，在一阶临界转速245附近，幅值出现一个高峰。如果考虑艉部结构影响，在低转速区域，轴系受到的不平衡力比较小，振动幅值与不考虑艉部结构影响时相比略有减小。随着转速的增加，在一阶临界转速区域出现局部峰值.与不考虑艉部结构影响的轴系振动特性图相比，其一阶临界转速略有降低，共振转速为 237，且在该转速下的局部峰值也略有降低，这是由于艉部结构对于艉轴振动系统起到一定的减振作用。

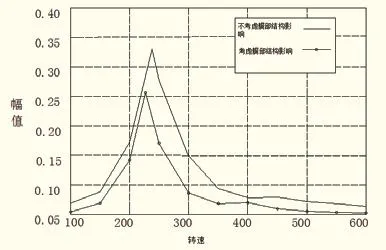
图6 艉部结构固有频率对轴系振幅影响关系图

3.3 艉轴架固有频率分析

把螺旋桨、轴系、前艉轴架以及后艉轴架看做一个整体，并将该整体简化为弹性支座上的连续梁结构。建立固有特性理论分析模型如图7和图8所示。将螺旋桨看做一个均匀的圆盘，将轴系与艉部交界的耦合水密支撑看做固定支撑约束，与此同时将前艉轴架以及后艉轴架的轴架臂看做两个弹性支座。

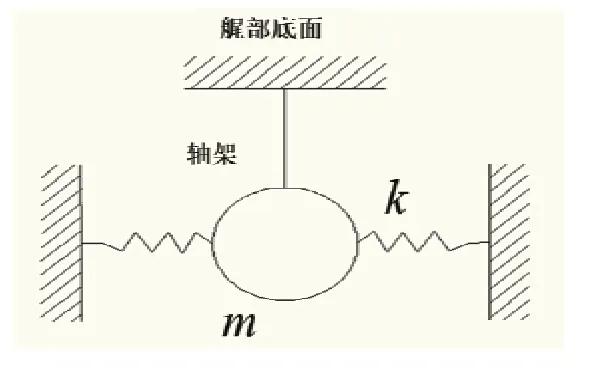
图7 轴架固有特性模型

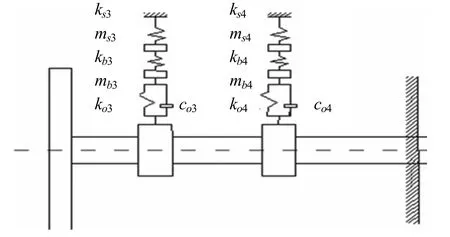
图8 艉轴固有特性理论分析模型

从耦合系统模型中选取艉轴架系统模型定义为分析子集，采用Guyan缩聚法对艉轴架固有频率进行计算。这样既考虑了船体对艉轴架系统的作用，又规避了船体结构产生的大量局部模态的影响。用这种方法分别求解子集的单臂艉轴架、双臂艉轴架、整体横向一阶固有频率。具体情况见表2。

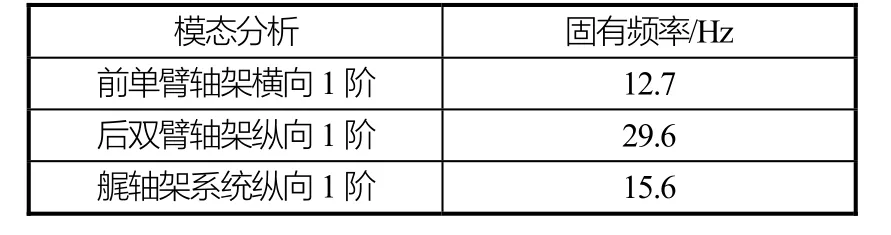
表2 艉轴架模态分析结果

本次分析也分2种情况讨论，考虑艉轴架的影响和不考虑艉轴架的影响。本次分析暂时忽略艉部结构固有频率对轴系振动的影响，具体情况见图9。从不考虑艉轴架的影响出发，分析结果与不考虑艉部结构的影响一致。若考虑艉轴架整体横向一阶固有频率的影响，从图 9可以得出一阶临界速度为240 r/min，低于不考虑艉轴架影响时的情况，且局部幅值低于不考虑艉轴架的情况。与考虑艉部结构相比，两者之间的数据差别并不是很大，说明两者对轴系都起到了一定的减振作用。

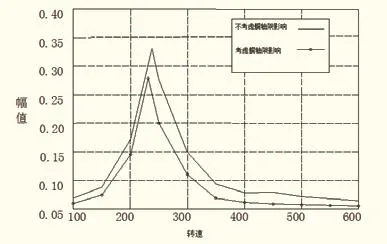
图9 艉轴架固有频率与轴系振幅关系图

3.4 艉部结构与轴承耦合刚度对轴系振幅分析

使用某船舶的实际参数来分析耦合刚度，其中艉部结构局部刚度为1.224×109N/m。

为了更好地研究艉部结构支承刚度对轴系振动的影响，需要将上文求得的艉部结构和轴承支承耦合刚度间0.35×108N/m往两端各扩展两个，然后根据固有频率的求解公式，分析在不同耦合刚度下，艉部结构与轴承支承耦合刚度与轴系振动固有频率之间的关系以及轴系的振动幅度随螺旋桨转速的改变的变化规律，从中找到轴系振动和艉部结构的内在联系。艉部结构与轴承支承耦合刚度与轴系振动固有频率之间的关系见表3和图10。

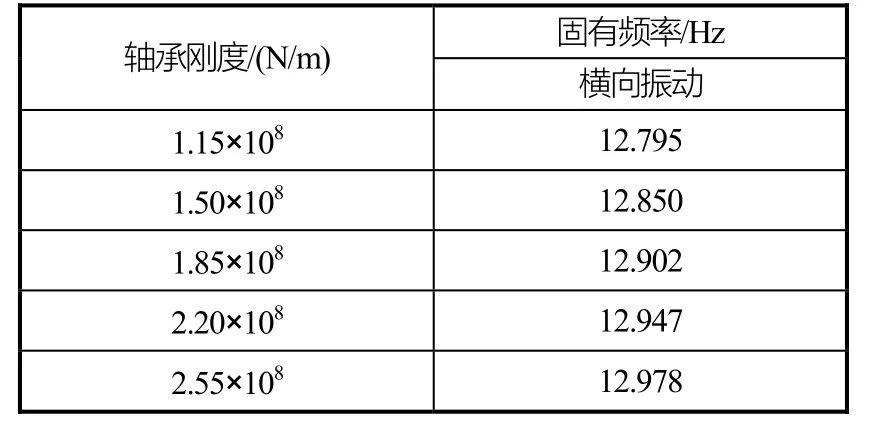
表3 艉部结构耦合刚度对轴系固有频率的影响

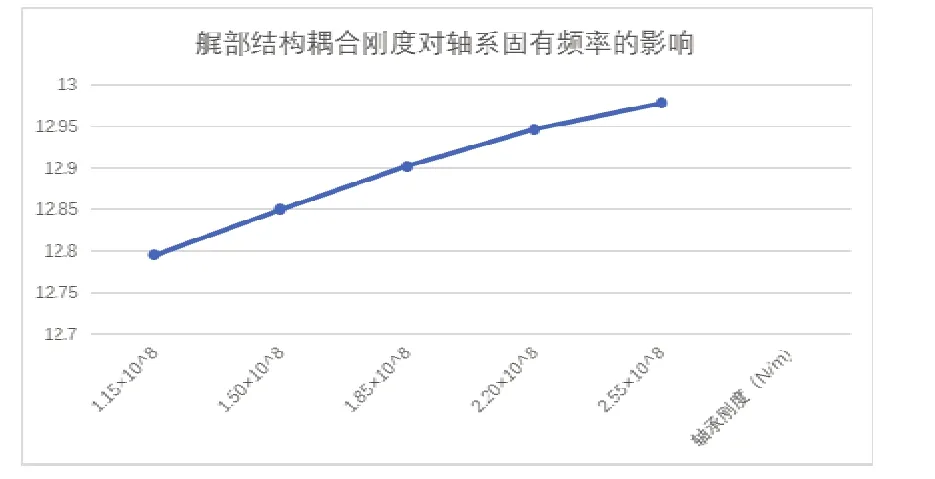
图10 艉部结构耦合刚度对轴系固有频率的影响

由图10可知如果耦合刚度增加，轴系振动横向固有频率也在增加，但是5个点之间的变化规律都比较小。随着耦合刚度的增加，固有频率增长速率趋于平缓。

艉部结构与轴承支承耦合刚度与轴系振动幅值之间的关系见图11。

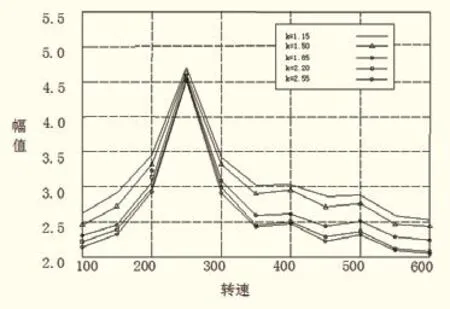
图11 艉部结构与轴承支承耦合刚度与轴系振动幅值关系图

由图11可知，在柴油机运转的初期，轴系的振动幅值急剧增加。在 200 rad·s-1～400 rad·s-1之间，各耦合刚度所对应的振动幅值达到最高点。然后随着转速的增加，幅值急剧降低然后趋于平稳。所以船舶在加速过程中必须尽快跳过该阶段，以免轴系和艉部结构发生不必要的损坏。从图11得出另一个结论是，耦合刚度越小，振幅越大。如果刚度低于一个极限值，轴系的振动幅度就会急剧增加。因此，计算并分析艉部结构与轴承支承的耦合刚度，对降低轴系的振动有十分重要的意义。

4 结论

本文研究了艉部耦合刚度以及固有频率对轴系振幅的影响，但是由于时间紧缺以及操作技术的不足，在研究固有频率对轴系振幅影响时，转速达到一个较高值有限元仿真系统并没有获得油膜涡动的准确数据，而是十分杂乱无章的数据。因此本文只局限于研究固有频率与振幅的关系。在研究耦合刚度对轴系振幅影响时，由于不能忽略轴系尾端螺旋桨的质量以及轴系本身的质量，对艉轴架、艉轴承油膜刚度的分析过于复杂。只能分开讨论艉轴架耦合刚度、艉部结构耦合刚度对轴系振幅的影响。

下阶段需要整体讨论艉轴架，艉部结构与轴系振动的关系，并且为了使仿真数据更加接近实际情况，综合考虑轴系与螺旋桨质量等对油膜刚度的影响，以获得更完善的分析数据。