线性转化的比估计量在数量特征随机化回答技术中的应用

李珊珊，努恩吉雅

(河套学院理学系，内蒙古 巴彦淖尔 015000)

Greenberg 1971[1]年提出了调查定量的敏感问题的随机化回答方法，例如调查职工平均额外收入多少，偷税金额等，之后许多学者对定量敏感问题模型进行了改进，包括借助辅助信息来提高估计敏感变量的精度。文献[2]在2006年使用了比估计提高了Warner模型的效率。文献[3]在2007年结合回归分析提高了一般化随机装置的效率。文献[4]在2008年提出了双辅助信息敏感问题问卷调查技术。文献[5]研究了使用辅助信息提高属性特征随机化回答技术的效率。本文探讨了在数量特征敏感问题的随机化调查中利用线性转化构造比估计量来提高精度的问题。当总体的辅助变量已知时，利用样本中的最小值和最大值通过线性转化构造了比估计量，在一定的条件下，提出的估计量效率较高。

1 Greenberg模型

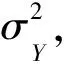
敏感性问题的均值μY的估计为

估计量的方差为

(1)

2 比率估计量用于Greenberg模型

随机化装置盒中有外形相同的两类卡片：

1)敏感属性值Y，辅助信息值T；

2)非敏感值X，辅助信息值T。

然后将卡片(a)、(b)以预定的比例p和1-p放入一个盒子中，回答者做出回答(z1，t1)，(z2，t2)，…，(zn，tn)。

根据矩估计和比估计的方法μY的估计量为

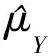
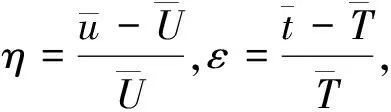
ER和VR为随机化装置的期望和方差，Ed为抽样设计的期望。

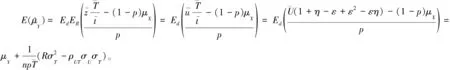
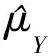
(2)

其中

证明：

3 线形转化及其比率估计量

假定指导辅助变量t的最小值为tmin和最大值为tmax，那么利用这些值，可以把辅助变量转化成两个新的辅助变量，分别为

进行线性转化之后，使用两个转化后的辅助变量可以得出总体均值μY的两个比率估计量

根据矩估计和比估计的方法，得到μY的两个估计量为：

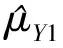
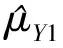
(3)

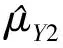
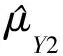
(4)

4 效率比较

4.1 比较3个比率估计量的偏差的大小

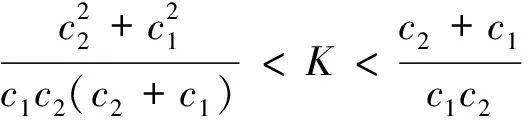
4.2 比较比率估计量的均方误差的大小

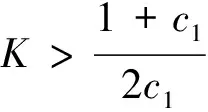
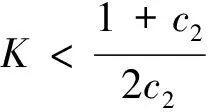
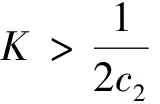
综上可以得出如下结论：

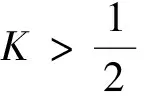
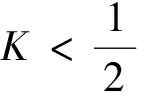
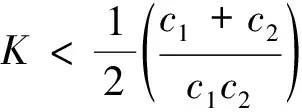
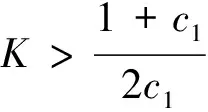
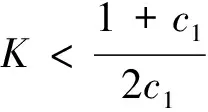
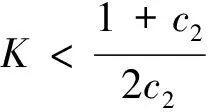
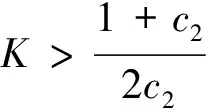
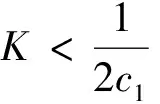
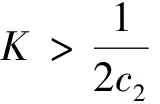
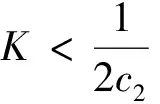
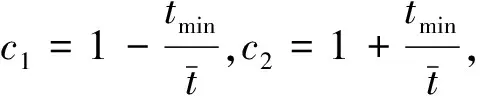
4.3 结论

结合上面的不等式和上面的12个结论，对于辅助变量与敏感变量呈正的相关关系，可得到结论：

通过以上结论，可以在实践中根据不同的情况选择更加优良的比率估计量。

5 数值模拟

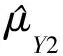
表1 估计量的均方误差

从数值比较结果可以得出结论：提出比率估计量的均方误差在参数一定的条件下优于Greenberg模型的效率，提出的3种比率估计量在参数不同的条件下，比率估计量的精度也有所不同，验证了第4部分理论比较的正确性。