二自由度阻尼机械振动系统仿真设计程序研究

陈玲琳，陈 奇

(1.安徽工业经济职业技术学院机械与汽车工程学院，合肥 230051；2.合肥工业大学机械工程学院，合肥 230009)

1 关于机械振动原理分析

1.1 Matlab Simulin功能简介

Matlab Simulin是在Matlab框图设计环境下应用的，主要应用于各类机械系统仿真与建模，它的建模范围广泛，可以用于任何通过数学表述的系统的建模[1]。比如动力学系统的航天系统等。其中还包含离散、事件驱动与混杂系统等。Simulink还提供了运用鼠标拖放对系统建立图型界面的方式，以及功能较完善版块和专业不同版块的集合，应用Simulink基本能够做到不必书写代码就能完成整个系统的建模，除此之外，Simulink还有一个重要作用是支持Stateflow，从而对事件驱动过程进行仿真。

1.2 阻尼振动物理模型分析

物理学中的机械振动一般分为了3种振动，阻尼振动、简谐振动与受迫振动。本文主要对阻尼振动做具体分析。

如图1所示，倘若黏滞阻尼对在x轴上的弹簧振子产生一定的作用力，就会使得弹簧振子产生一定的阻尼振动。假设此弹簧振子受到阻尼力

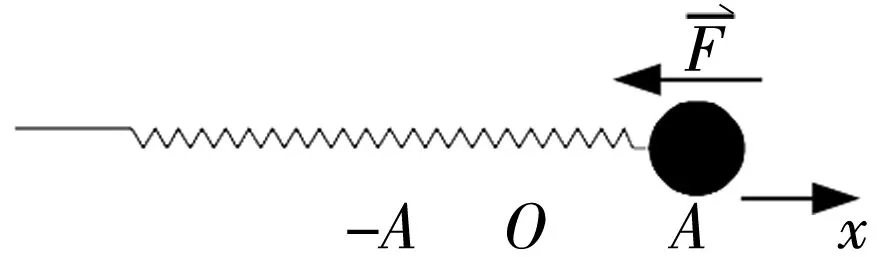
图1 弹簧阻尼振动物理实验模型示意图

(1)

(2)

通过整理后得到式(3)：

(3)

(4)

式(4)为阻尼振动方程式。它的解x就是弹簧振子在t时刻的振动位移，一阶导数x′就是弹簧振子在t时刻的振动时速，它的二阶导数x″就是弹簧振子在t时刻的加时速。

1.3 Matlab SimulinK仿真方法分析

Matlab仿真方法是通过其强大的分析功能对微分方程组的数值积分，它能够提供多个不同的积分方法，而这些不同积方法均有着不一样的功能与使用范筹以待选择。对于ODE的Sover(解题器)，采用数值方法对每一道程序步骤的解进行计算，同时还要对它的解能否符合给予的允许范围内的误差进行检验，如果符合，说明求得的解是对的，否则就需要退回重新进行计算，直到得到正确的解为止[2]。指令格式：

[t，y]=solver(‘F’，tspan，yo)，

(5)

式(5)中，积分方法由solver表示，F为微分方程ODE文件名的表述，为了对能够便于对解题器进行调用，建立指令格式为：

Fumction ydot=F(t，y)。

(6)

ydot=[表达式1；表达式2；表达式3；表达式4；……]其中表达式“n”以列向量的方式构成系统的状态方程；tspan表示一个行向量，主要对计算的起止时间进行表述[to，te]；yo表示刚开始的状态值，通过运用列向量进行表示，维数为状态向量数。Matlab控制系统工具箱时域响应函数构成如图2所示。

图2 Matlab控制系数工具箱时域应主要函数

上述函数既可以是状态方程形式，也可以是传递函数的形式，因此对于线性系统，除了对解题器进行仿真，还可以依据控制系统和振动系统的数学模型的统一性，对问题的相似性进行研究，可以通过借用Matlab控制系统工具箱函数对其进行仿真，从而为机械振动系统仿真分析提供一个分析功能较强，使用起来方便的工具[3]。

2 机械振动系统的仿真程序设计

关于单身由度振动系统，动力学方程

(7)

取X1=X，X2=X，那么式(7)中

X1=X2，

(8)

X2=-f(x1，x2)+p(t)

(9)

在式(8)与式(9)构成的方程中，对相应的微分方程解题器调用时域仿真，通过最终的结果值采用绘图命令plot对相平面的相轨迹与变化曲线进行描绘。

关于多自由度线性机械振动系统，它的矩形方程就是通过动力学方程形式进行表达的，n自由度振动系统的动力学方程为

MX+CX+KX=F(t)，

(10)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵，都属于方阵(n×n)；F(t)为作用于n个自然度的外激励作用力；X表示n个自由度的位移变量，换句话说就是由n个二阶微分方程构成的动力学方程。当前把各质量的位置移动与速度都看成比较独立的变量，使原来的动力学方程变成2n个一阶微分方程组成的状态方程，把原系统响应的振型叠加法换成状态变量分析法，补充式(11)为：

MX=0 。

(11)

整理式(10)和式(11)得

AY+BY=CF(t)，

(12)

Y=AY+BF(t)，

(13)

式中，A=-A-1B为系统矩阵，B=A-1C为控制矩阵。

假设系统的输出由Z表示，Z可以是系统各处的位移、速度或作用力，Z与Z的向量维数均由实际的研究对象确定。Z可由输入状态与激励进行任意组合为：

Z=C′Y+DF(t)，

(14)

式中：C′表示输出矩阵；D表示直接传递矩阵。

由式(13)与式(14)构成了多个输入出的线性振动系统的状态空间表现形式，系统简记为A、B、C′、D。对于此状态空间表现形式取拉氏变换，可以定义输出响应与输入激励之比为多自由度线性振动系统的传递函数矩阵为

(15)

式中：A和I属于同一阶单位的矩阵；G(s)表示所有多自由度振动系统特殊的性质，其各构成元素成为它所对应的传递函数。

由线性振动系统的状态方程与传函数，对振动系统的分析，可通过控制理论实施，使得Matlab控制工具箱能够较好地适应振动系统，工具箱函数的作用是较方便仿真设计。Matlab控制系统工具箱函数处理MIMO系统基本原理是SISO系统之叠加组合[4]。

3 振动系统的仿真分析

3.1 构建二自由度机械振动系统模型

如图3所示为带黏性阻尼二自由度振动系统。

m1，m2：小车质量；c1， c2：阻尼系数；k1， k2：弹簧强度；y1，y2：小车的位移图3 带黏性阻尼二自由度振动系统模型示意图

依据机械振动系统原理能够得出系统动力学表达式为

(16)

通过整理可得式(17)矩形方阵式：

(17)

再通过简化可得式(18)：

(18)

(19)

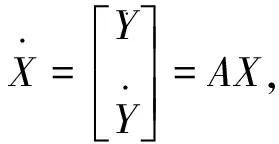
(20)

式中A是表示系统矩阵，

(21)

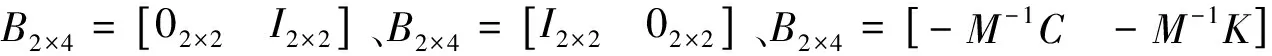
3.2 二自由度阻尼机械系统仿真

振动系统仿真选择二自由度阻尼机械系统进行仿真分析。为了对二自由度阻尼机械系统的仿真更加精准，需要对系统的主要参数进行提取，比如m1与m2所表示的系统的小车质量，c1与c2阻尼系数，以及系统各种初始的条件，然后依据相关问题对系统进行仿真设计程序分析。系统取出相关参数见表1。

表1 系统取出各相关参数汇总表

通过表1取出系统相关参数可得以下系统矩阵：

(22)

为了防止出现计算错误，此处的系统矩阵A不进行相关计算，而是使用不但计算速度快，而且计算准确的Matlab软件来进行相关计算。此文运用Matlab软件ode450(求解器)，对相关微方程进行求解，计算出微方程数值解，再凭借plot0(绘图指令)，绘制出二自由机械振动系统仿真图形，之后通过仿真图对系统展开研究[5]。

经过Matlab软件编程命令窗口发出指令，之后直接指挥仿真系统进行正常工作，此外，该软件编程还运用了M文件进行编辑，M文件由脚本文件编程与函数文件编程两部分构成，此文为了减少失误的情况发生，以及提升读者的方便性，使用了函数文件编程[6]。

Matlab软件源程序如下：

为了建立求系统状态方程的M文件，编译完成之后要保存以下命令。

Function xdot=zdot(t，x)

Global K1 K2 m1 m2 c1 c2；

K1=4；K2=2；m1=1；m2=9；c1=0.2；c2=0.5；

设定振动系统参数。

xdot=[-(c1+c2)*x(1)+c2*x(2)-(k1+k2)*x(3)+k2*x(4)]/m1；

[c2*x(1)-c2*x(2)+k2*x(3)-k2*x(4)]/m2；x(1)；x(2)]；

由于篇幅的关系，其他有关主函数指令在此就不再进行分析。

在使用Matlab软件时，经命令窗口录入相关程序，再按回车键，机械振动系统仿真图就会展现出来，如图4所示。

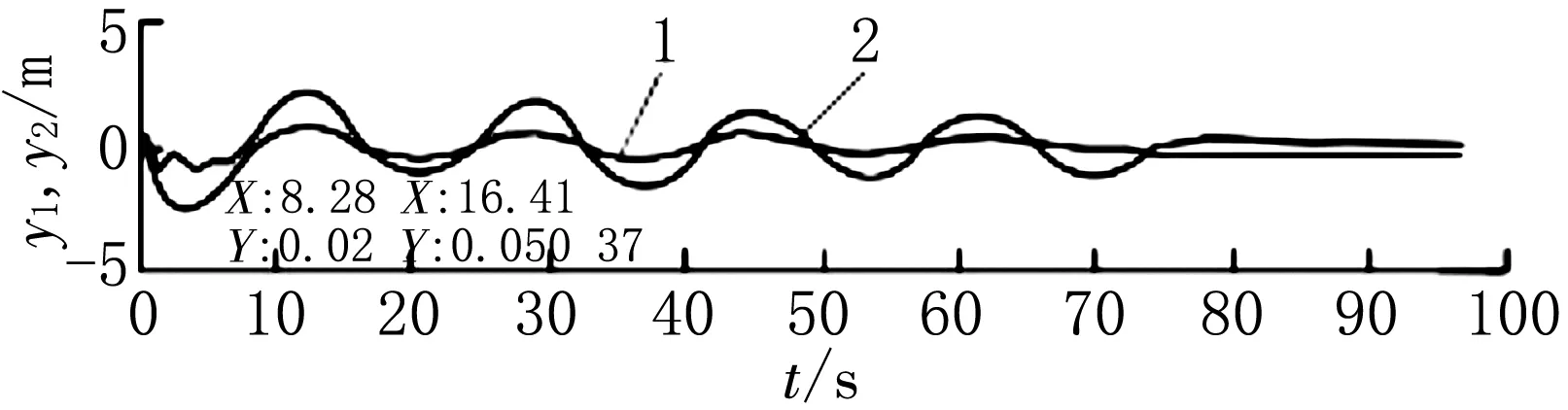
1.位移y1；2.位移y2图4 物体m1，m2的位移仿真

依据仿真最后结果，我们可知m1，m2两个物体频率一样，它的稳态响应与同频振动响应应为同一响应，由此能够清楚地看出因为m2带动m1振动，在t为8.28s时，m1，m2位移变化应达到了同步，因此能更清楚地知道系统的固有频率[7]。但是为了掌握m1，m2的速度变化，m1，m2最高速与时该已明确了，就能够对程序变化做进一步了解，做出振运系统速度仿真图，如图5所示。

通过图5可知，物体m1在m2的带动下，其反向最快速度可达2.38 m/s，然后在1.93 s内正向最高速为1.06 m/s，再之后，大约在16.24 s左右时，m1与m2两者速度几乎一样，没有多大差距了。同理，要对其加速度的变化进行深入了解，改编程序后，结果如图6所示。

依据图6知道，物体m2带动物体m1，刚开始反向最大的加速度6.33 m/s2，然后快速地在大约1.21 s时，进入最高加速度大约为4.20 m/s2。当然用同样的方法，还能够对m1与m2受力状况进行分析。

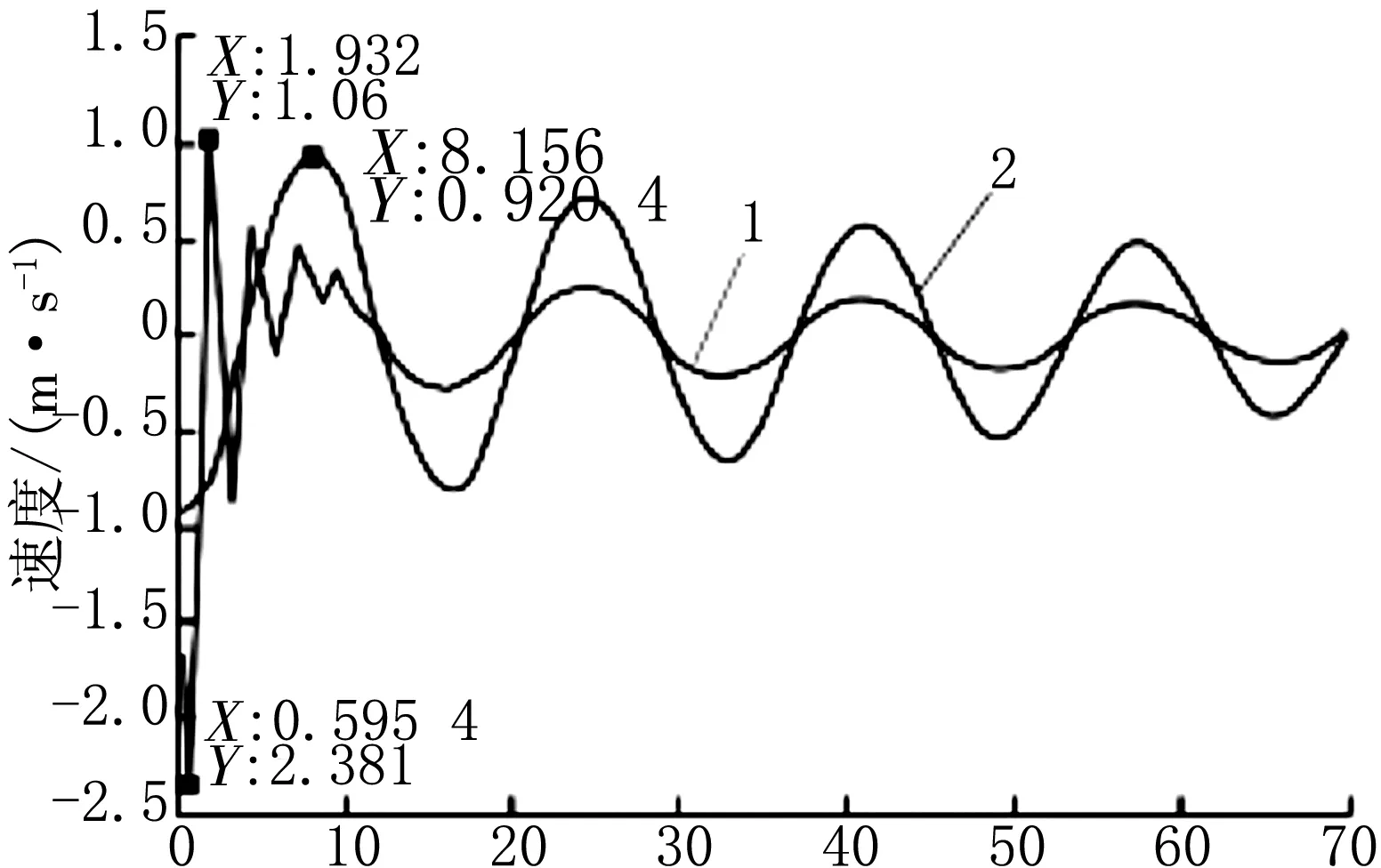
1.速度V1；2.速度V2图5 物体m1与m2的速度仿真

1.加速度a1；2.加速度a2图6 m1与m2的加速度仿真示意图

4 结语

文章以机械振动原理为论文理论依据，对机械振动系统仿真程序设计进行探讨，最后选择二自由度阻尼振动系统作为研究对象，对其建模与仿真进行详细分析，获得振动系统的运动规律。