基于ANSYS Workbench的O型密封圈接触分析

李修宇，张传俊

(安徽工商职业学院，合肥 230022)

0 引言

由于O型密封圈具有结构简单、制造和使用方便、价格低廉等特点，因此，被广泛地应用于机械设备的液压密封和气动密封中[1-2]。除上述特点外，O型密封圈还具有良好的密封性，既可用于静态密封，也可用于动态密封，既能单独使用，也可以采用组合式配合挡圈密封，而且工作压力可在0.1～400 MPa，温度范围可在-60 ℃～200 ℃，范围较广。O型密封圈的密封性能依靠系统压力实现自动双向作用密封，并随系统压力的提高而增大。密封性能直接决定其能否正常工作，因此，需要对其进行研究。

文献[3]提出一种有限元分析模型，对O形圈密封结构在不同油压和压缩率作用下的应力分布及接触压力分布进行具体分析，根据分析结果对O形圈密封结构的适用条件进行总结，得出的结果为密封圈的安装提供了一定的指导。但是该方法在分析过程中引入了比较多的参数，对这些参数进行拟合具有一定的难度，因此，该方法的应用性不强。文献[4]构建了一个带副唇的旋转轴唇形密封接触分析模型，运用该模型对密封圈装配后的不同压缩量与旋转轴的接触应力进行分析，得出旋转轴唇形密封圈装配后的压缩量应该保证在0.7 mm以上的结论。虽然该方法得出了较为准确的结论，但是该模型应用范围有限，不适合大范围使用。

为了对传统方法进行完善，基于ANSYS Workbench平台，对O型圈密封接触进行分析。

1 O型圈有限元模型的建立

选用的O型密封圈型号为乙烯—丙烯橡胶，橡胶材料是超弹性材料，具有非线性特征，ANSYS Workbench平台中有很多橡胶参数模型，采用Neo-Hookean超弹本构模型，其应变能函数可以表示为

(1)

式中：W为应变能；λ为橡胶伸长率；J为变形后体积与变形前的体积比值；μ为材料的应力量纲，为常数，μ=ρkT，其中ρ为密度，k为Boltzmann常数，T为温度；I1为Cauchy-Green变形张量的第一不变量。材料的属性[5-6]见表1所示。

表1 材料属性

由表1得出橡胶单元的Initial Shear Modulus Mu为1.3 MPa，Incompressibility Parameter D1为1.52 MPa-1。

分析模型由活塞、缸体和密封圈组成，由于模型是圆周对称的，可以对模型进行简化，将三维模型简化为二维轴对称。橡胶在压缩过程中将产生大变形，为让结果更快收敛，活塞和缸体采用高阶单元，O型圈采用低阶单元并采用四边形网格进行划分，模型共包括2 924个节点，961个单元。划分网格如图1所示。

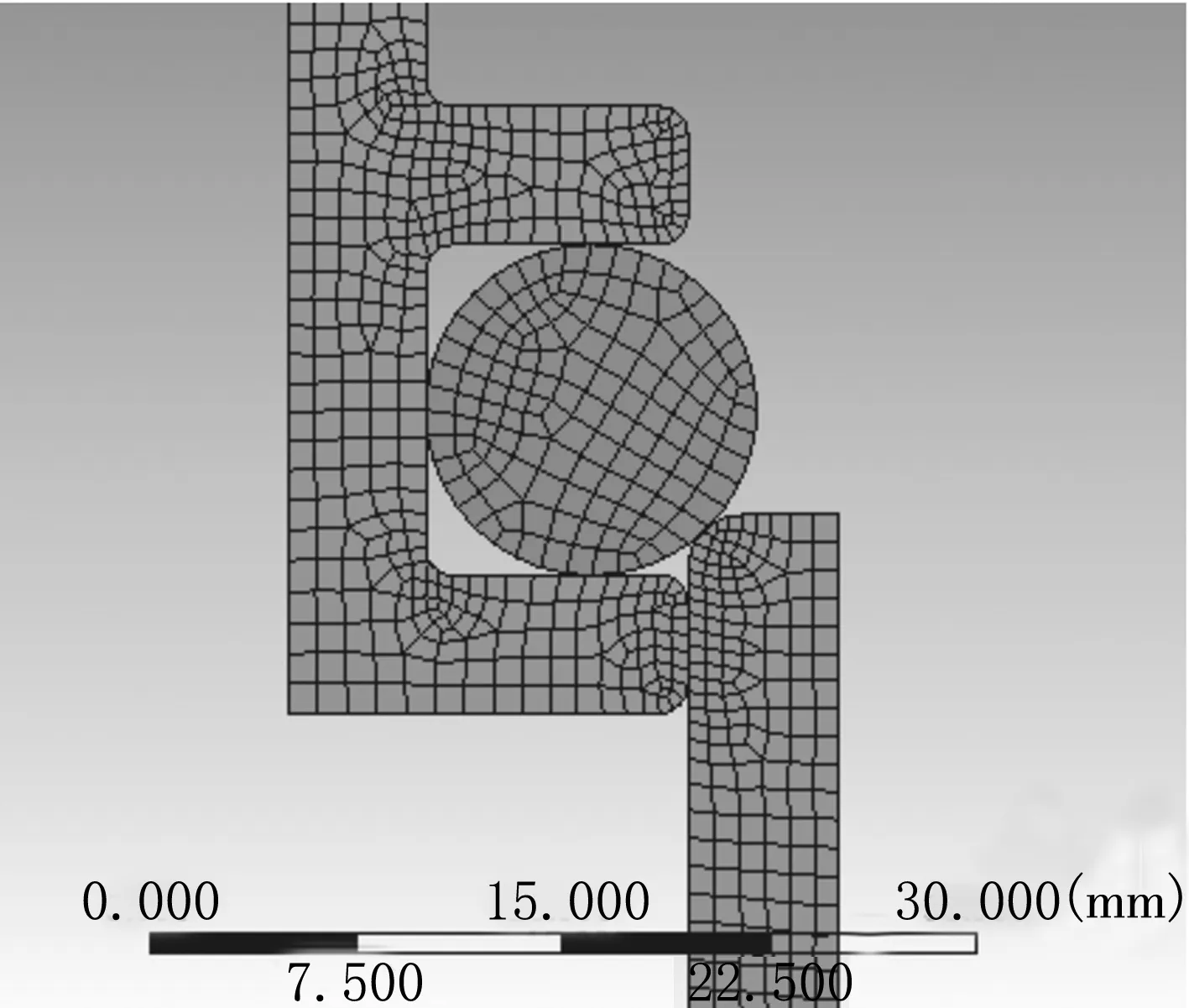
图1 二维模型网格图

在Workbench中采用接触单元模拟接触问题，建立活塞、缸体和O型密封圈之间的接触关系，活塞与缸体的接触形式采用无摩擦接触；材料的刚度相近，采用对称接触；接触算法用拉格朗日法，并用高斯点的探测方式，强制更新刚度。活塞与O型密封圈、缸体与O型密封圈采用相同的接触关系，采用摩擦接触，非对称接触，法向接触刚度取3，并且每一步计算都要进行刚度更新。

分析计算设置20个载荷步，约束缸体底边轴，释放X轴约束；约束活塞顶边向Y轴负方向20 mm，给活塞一个向下的位移，模拟O型密封圈在不同的压缩率下，其密封状态和失效形式。O型密封圈压缩率α的计算公式为：

(2)

式中：d为O型密封圈压缩前的直径；h为O型密封圈压缩后的直径。

2 仿真结果与分析

目前对于密封圈仿真结果评价的方式较为统一，采用等效应力评价O型密封圈的疲劳和破损失效，采用接触压力评价O型密封圈密封性能，即最大接触压力大于工作压力。图2为O型圈压缩率为20%时的等效应力云图。图3为接触压力随载荷步的变化曲线。

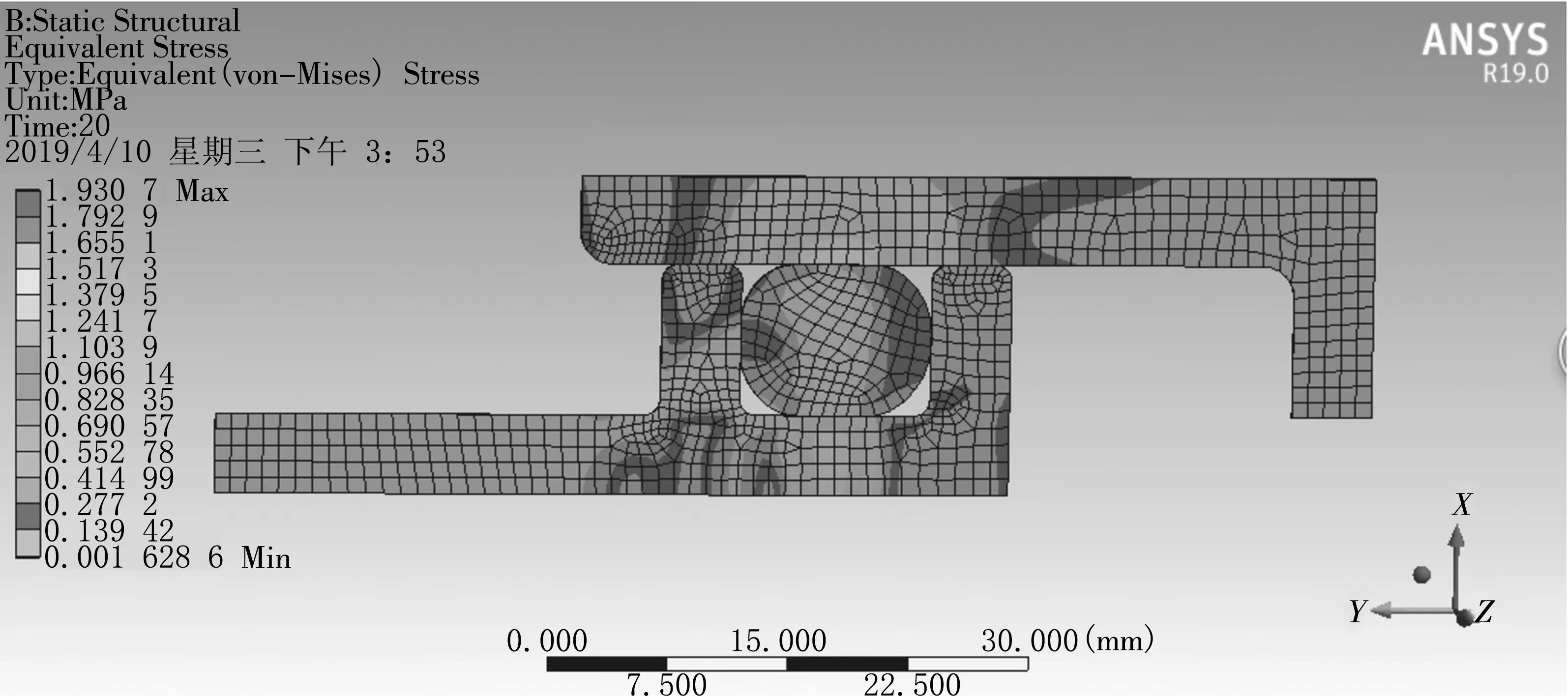
图2 等效应力云图

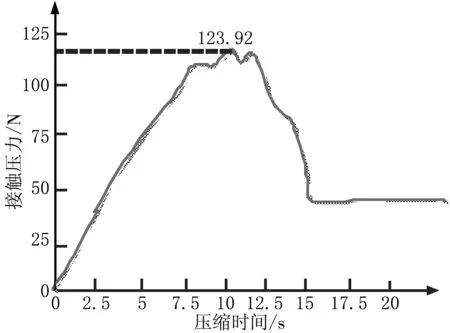
图3 接触压力曲线

由图2的云图可以看出O型密封圈的应力分布是对称的，活塞和缸体接触的X向应力较大，最大应力发生的位置是活塞沟槽侧壁，若沟槽的表面粗糙度较差，会引起O型密封圈的疲劳和破损。由图3可以看出在活塞压缩缸体的过程中，最大的接触压力为123.92 N，能够满足密封条件。

利用ANSYS Workbench平台分析O型密封圈在不同压缩率情况下的等效应力分布和接触压力。分别计算压缩率在10%、15%、20%、25%和30%情况下的规律曲线，得出图4～5等效应力和接触压力随压缩率的增加呈现线性增大的趋势。

图4 等效应力与压缩率关系

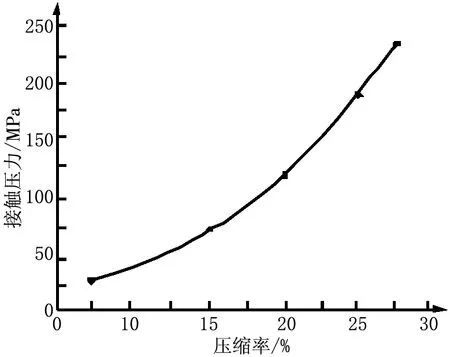
图5 接触压力与压缩率关系

3 结语

为了分析O型密封圈的接触变形情况，根据实际工作情况建立了二维轴对称非线性模型，根据模拟工作过程情况得出了O形密封圈的等效应力云图和接触压力分布，并绘制出等效应力和接触压力随压缩率的变化曲线。得出O形密封圈压缩率也会随着等效应力的变化而产生变化，同时，压缩率会随着接触压力的加大而提升，在活塞压缩缸体的过程中，O形密封圈的最大接触压力为123.92 N，能够满足密封条件，说明所提方法能够对O型密封圈接触压力进行准确分析，可以为选用O形密封圈提供参考。