差动式电热SMA驱动器设计及驱动性能研究

刘玉玺，路国平

(重庆工程职业技术学院机械工程学院，重庆 402260)

形状记忆合金(Shape Memory Alloy，SMA)是一种具有形状记忆效应的金属材料，其在相变回复过程中会产生很大的回复应力，具有高能量密度和良好的环境适应性等特性。国内外的很多学者对SMA材料的相变机理开展了广泛的研究，如Prasad等[1]通过向Ni49Ti36Hf15合金中加入Ta元素，改善了马氏体的脆弱性和不连续性，提高了形状记忆合金在高温下的工作能力。Ko等[2]从分子动力学角度解释了温度和应力诱导马氏体相变的机理。Yazdandoost等[3]研究了晶格层错能对奥氏体相力学参数的影响，为研究在具有晶格缺陷状况下SMA的属性提供了指导。

正是基于这种特殊效应，SMA已在汽车[4]、航空航天[5]、医疗[6]等多个领域得到应用，而用SMA制作的驱动器也是工程应用领域研究的热门。如许红伟等[7]进行了形状记忆合金(SMA)弹簧驱动器的变形研究，建立了电加热情况下的SMA弹簧温度变化模型，并得到了驱动时间与弹簧温度的关系曲线。于东等[8]利用形状记忆合金单程记忆效应，提出了一种基于应变约束条件的旋转驱动器的结构设计方法。李杰锋等[9]设计并制造了一种线性驱动器，并通过试验验证了其可实现往复双程运动。但现有的研究主要集中在驱动器的单程或双程运动，而对具有双向双程作用并具有低频振动驱动特性的SMA驱动器的研究还较少。本文首先根据形状记忆合金的记忆特性和温度相变过程，设计制作了差动式双向电热SMA驱动器，并建立了驱动力方程，然后通过实验研究了电流和温度对驱动器的驱动速率和位移的影响，并将理论结果与实验结果进行了对比，分析了误差产生的主要原因。

1 电热SMA驱动器结构设计及参数确定

1.1 差动式电热SMA驱动器结构设计

以普通螺旋弹簧为偏置元件，以NiTi形状记忆合金(NiTi-SMA)为驱动元件，设计的电热SMA驱动器的结构如图1所示，可以实现双向直线驱动。驱动器的外观尺寸是：65 mm×45 mm×10 mm。SMA螺旋弹簧丝直径为0.8 mm，弹簧直径8 mm，有效圈数8圈。采用普通电流进行加热和断开，可实现驱动器的往复运动；采用脉宽调制法(PWM)电流进行加热，根据所需动作频率的大小，调整电流脉宽和电流大小，可实现往复的震荡运动。

自然状态下，未通入电流时，SMA弹簧在普通弹簧的偏动力作用下被拉长；当电源被接通后，由于2个SAM弹簧自身的电阻特性，SMA弹簧被加热。当温度达到相变温度时，发生马氏体逆相变，SMA弹簧收缩变形，在变形回复力的作用下，实现直线驱动；当电源断开后，在普通螺旋弹簧偏动力的作用下，导向杆又回到初始状态，通过电源的接通、断开，从而实现驱动杆往复的直线运动。

图1 差动式电热SMA驱动器装配图

1.2 驱动元件参数确定

由于在设计电热SMA驱动器时，SMA螺旋弹簧的相关参数已知，因此只需选取合适的普通弹簧就可。首先采用推拉测力仪，测取SMA螺旋弹簧在低温下拉伸10 mm时的拉力大小为1.2 N；其次，根据所选用的SMA螺旋弹簧的力学性能可知，处于高温状态时的最大回复力为4 N。因此，可计算出普通弹簧的直径D为6 mm，丝径为0.6 mm，有效圈数为16圈，节距为3 mm，初始状态时压缩量为2.5 mm时处于平衡状态。另外，由差动式驱动器的工作原理，可以求得普通弹簧的弹性系数及剪切弹性模量。

初始平衡状态时：

1.2·2=kp·2.5，

(1)

由式(1)可得所采用的普通弹簧的弹性系数为kp=0.96。

高温平衡状态时：

4·2=kp·l，

(2)

式中：kp为本文所选用的普通弹簧的弹性系数；l为普通弹簧的压缩量。

由式(2)可得驱动器在高温平衡状态时，普通弹簧的压缩量：l=8.3 mm。因此，可知本文所设计的驱动器所能驱动的最大位移为δmax=5.8 mm。

把相关参数代入弹簧设计理论公式

(3)

式中G为SMA螺旋弹簧的剪切模量。

2 电热SMA驱动器动力方程

随着温度的变化，SMA弹簧的弹性模量不断发生变化，马氏体相的弹性模量远远小于奥氏体相的弹性模量，因此，要研究SMA的动力学问题，首先要做如下的假设：1)SMA样品内部应变ε、应力σ、温度变化、普通弹簧的弹性率变化均匀；2)忽略加热时热量的损失；3)忽略导向杆、弹簧及动板的质量，以及导向杆与固定板间的摩擦力；4)在运动过程中，驱动器一端没有位移，另一端始终有伴随着负载的位移、速度、加速度。

在被加热到低于或超过相变温度时，SMA螺旋弹簧的剪切弹性模量也会随之变化。

当温度低于相变温度时，加热过程中SMA剪切弹性模量与温度的关系为

(4)

当温度高于相变温度时，加热过程中SMA剪切弹性模量与温度的关系为

(5)

式中：GL、GH为SMA弹簧在低温和高温下测得的剪切弹性模量，分别为GL=7.5 GP，GH=25 GP；T为温度；Tm为相变温度参考值，温度低于相变温度时为58，高于相变温度时为40。

基于前面的假设可以得出，驱动器在运动过程中驱动力的大小为

Pq=2P-kp·δ，

(6)

式中：Pq为驱动器输出的驱动力；P为单个SMA弹簧的弹力；δ为驱动器的驱动位移。

本文所设计的驱动器，驱动力的大小是由SMA螺旋弹簧相变回复力提供的，在初始状态下，SMA螺旋弹簧处于拉伸状态，其拉伸距离为12 mm。假设初始状态时，驱动位移为0，那么当驱动器的驱动位移为δ时，则SMA螺旋弹簧的形变量为(12-δ)mm。将SMA螺旋弹簧的驱动力方程代入式(6)可得

(7)

式中：L0为SMA螺旋弹簧的初始形变量，本驱动器中L0=12；G0为初始状态时的弹性模量；Θ(ξ)为热弹性模量；ξS和ξS0由Brinson的相变方程求得[10]；γL为最大剪应变；下标”0”表示初始状态。

式(7)即为根据本文中所设计的差动式电热SMA驱动器的力学方程，在该方程中存在驱动力、驱动位移及温度3个变量。由公式(4)、公式(5)和公式(7)即可求得加热过程中驱动力与驱动位移及温度之间的关系。

3 电热SMA驱动器驱动特性测试结果分析

3.1 驱动电流对驱动速率的影响

在无负载状态下，驱动器驱动位移为2 mm，驱动电流随时间的变化关系如图2所示。从图中可看出，随着电流的增加，驱动时间迅速减小。当电流增加到3.5 A时，驱动时间仅需3 s。因此，在实际应用中，可通过调节电流的大小来改变驱动器的驱动速率。当电流<2.5 A时，驱动速率相对较低；而当电流>2.5 A时，随着电流的增加，驱动速率明显增加。以上测试结果说明SMA螺旋弹簧对大电流较敏感，小的电流变化即可引起较大的位移输出。但要注意的是，最大电流要根据具体选用的SMA来确定，电流过大可损害其记忆能力，并减少其使用寿命。而在满足使用要求的前提下，电流越小，越有利于延长SMA的使用寿命。

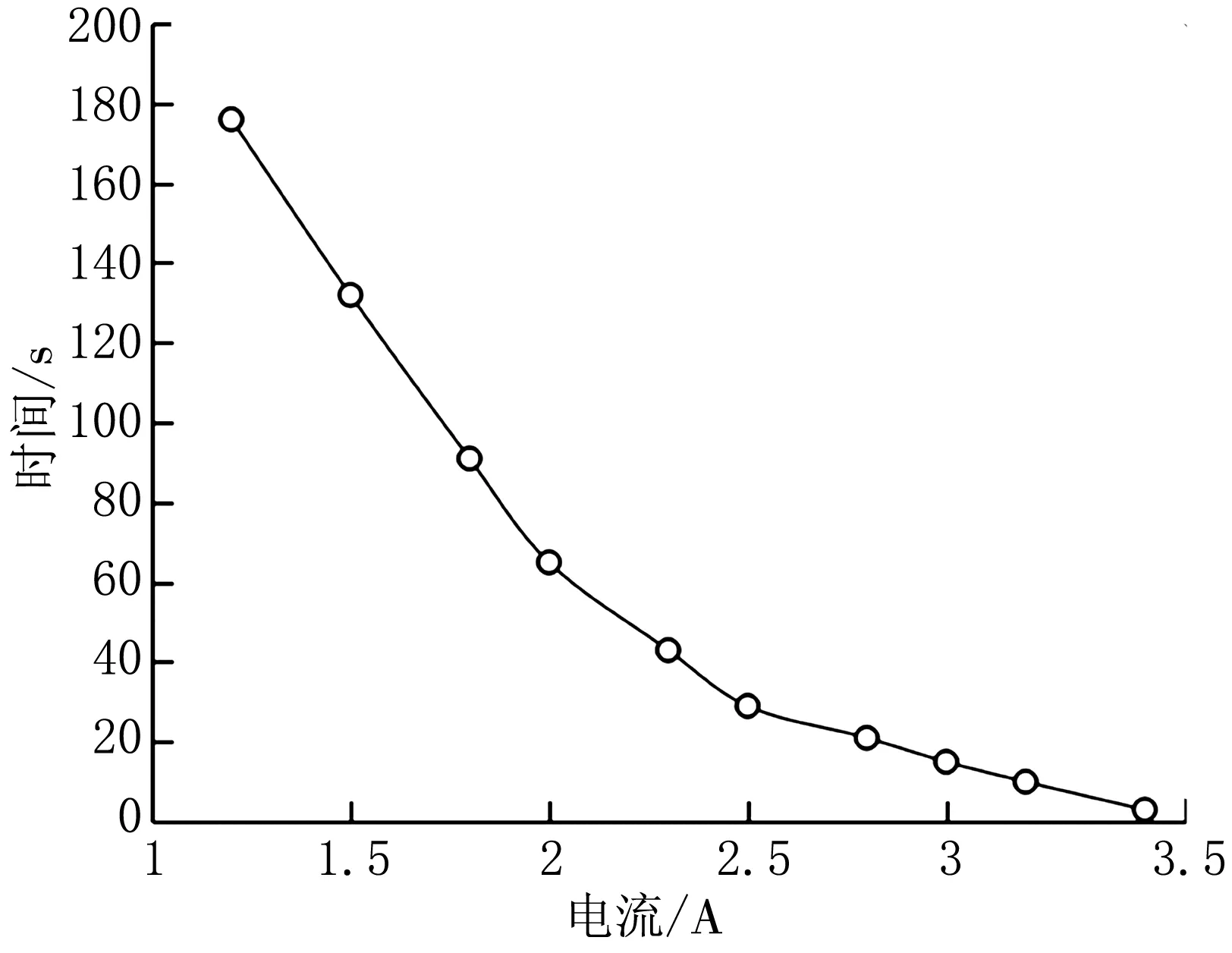
图2 驱动位移至2 mm，电流与时间之间的关系

3.2 温度对驱动位移的影响

给驱动器施加恒定的负载P=2 N，然后通入电流，并检测SMA螺旋弹簧的表面温度与驱动位移间的关系。不同温度下驱动位移的测试结果及驱动器力学模型理论计算结果的对比如图3所示。

从图3中的分析结果可以看出，只有当温度达到奥氏体相变开始温度时，才会有驱动位移，但在初始阶段的驱动位移的变化很慢，这是因为在相变初始阶段，SMA螺旋弹簧存在的应力诱发了马氏体相变，抑制了奥氏体的相变速率。由理论结果和实验结果对比可以看出两者的走向基本趋于一致，从而说明了所建立的差动式双向SMA驱动器驱动力模型的可行性，可为差动式SMA驱动器的设计提供理论指导。但理论值和实验值在各个相变温度点仍存在着一定的偏差，分析其可能的原因为：一方面是普通弹簧、SMA弹簧、动板及导向杆的重量没有被考虑在内；另一方面是导向杆在驱动过程中存在倾斜现象，增大了导向杆和固定板间的摩擦力。

图3 驱动位移与温度之间的关系(P=2 N)

4 结语

1)根据NiTi形状记忆合金(Shape Memory Alloy，SMA)的记忆效应，设计制作了差动式电热SMA驱动器，通过电流的通断可实现驱动器的往复运动及往复振动驱动。

2)根据SMA螺旋弹簧的力学模型及Brinson相变方程，建立了差动式电热SMA驱动器的力学方程，在该方程中可以更直观地表征驱动力、驱动位移及温度之间的相互关系。

3)无负载状态下的测试结果表明，驱动电流越大，驱动位移至2 mm所需的时间越短。当电流<2.5 A时，驱动速率相对较低；当电流>2.5 A时，随着电流的增加，驱动速率明显增加。

4)通过对不同温度下驱动位移的测试结果及驱动器动力模型计算结果对比分析可知，只有当温度达到奥氏体相变开始温度时，才会有驱动位移。并且理论计算结果和实测结果趋于一致，从而说明了所建立的差动式双向SMA驱动器驱动力模型的正确性，可为差动式SMA驱动器的设计提供理论参考。