基于弹性理论的功能梯度材料管板应力分析
(1.东北石油大学 机械科学与工程学院,黑龙江大庆 163318;2.中石化石油机械股份有限公司,武汉 430205)
0 引言
工业生产的高参数化使得换热器的服役环境日渐苛刻,换热器的管壳程温差的逐渐加大,使得单一材料的管板无法满足工艺要求[1],使用层合的复合材料管板[2-6]也可能会出现层间开裂等失效问题。相比之下,功能梯度材料在制备过程中,结构两侧由不同性能的材料组成,但这两种材料并不直接相连,而是在它们之间形成一个在成分、组织及性能上呈现连续梯度变化的过渡区域,从而达到内部界面弱化、甚至完全消失,材料的宏观特性(如弹性模量、热膨胀系数等)在空间位置上呈现梯度变化,进而减小和克服结合部位性能的不匹配,以满足不同结构元件对材料使用性能的不同要求,达到提高承载结构能力并合理使用材料的目的[7],因此,功能梯度材料(Functionally Graded Materials,简称FGM)在换热器管板上具有广阔的应用前景[8-9]。目前,Ganczarski等[10]推导出了FGM厚板在热载荷作用下的平面应力状态;Ashrafi等[11-12]研究了厚功能梯度材料板的非线性动力响应和振动;李世荣等[13]研究了经典板理论下功能梯度板的自由振动响应问题和一阶剪切变形理论下功能梯度圆板与相应均匀圆板轴对称弯曲解的线性相似转换关系;Sui等[14]研究了四边简支的功能梯度层合板弯曲的一阶剪切变形理论解与相应均匀板弯曲的经典解的关系,并且给出了相应的转换关系的表达式。基于该材料的力学行为研究使得功能梯度板力学问题得到简化,对工程上功能梯度材料管板的设计与制造具有重要意义。基于此,本文利用物理中面的概念,将功能梯度管板中材料的各向异性问题转化到经典版理论中,从而求得功能梯度管板的应力分布。
1 弹性理论下功能梯度管板应力计算
当换热工艺存在较大温差时,通常选用U形管式换热器来减小温差应力,因此,功能梯度材料制备的换热器管板基本上都用在U形管式换热器上[15]。同时FGM管板作为复合材料管板,可能出现与筒体及管箱材料不同的情况,为便于连接,采用通过垫片与管箱法兰及壳体法兰连接形式的管板,即图1所示的a型,这样既便于设计,也便于加工制造。因此,以U形管式换热器中法兰连接且不兼做法兰的功能梯度管板为例,进行内压载荷下FGM管板的应力分析。

图1 管板的连接形式
1.1 功能梯度管板应力计算公式推导
1.1.1 幂函数模型
考虑到成分分布范围广泛以及材料加工时的难易程度,文中选用幂函数模型[16]。
(1)
式中fij——FGM成分分布模型函数;
xc,xp——两组分边界区位置;
β——梯度因子。
取FGM板z向为厚度方向,板的物性参数沿厚度方向呈梯度变化,将两种材料分别定义为材料1和材料2,根据幂函数模型表达式来表达功能梯度材料制备的换热器管板(以下简称FGM管板)的物性参数[16]弹性模量、线膨胀系数如下。因目前的功能梯度材料大多是陶瓷-金属或金属-金属,泊松比μ都相差不大,故可认为泊松比是与空间域无关的一个常量,即功能梯度材料的泊松比是一个常数。
弹性模量E(hz):
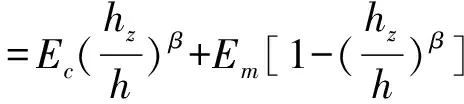
(2)
线膨胀系数α(hz):

(3)
式中hz——FGM板厚度方向的坐标,0≤hz≤h;
h——板厚度,mm;
c——下角标,材料1的物性参数;
m——下角标,材料2的物性参数。
1.1.2 基本求解方程
管板作为管壳式换热器的重要零部件,是一块开有多个密集小孔的圆平板。基于一个厚度h、半径R的功能梯度材料圆平板,并建立O-rθz柱坐标系,原点O与板的圆心重合,O-rθ面位于全金属相所在的平面,z轴垂直于该平面,材料沿z轴呈连续梯度变化,并作出以下假设:
(1)在FGM圆板中垂直于中性面的平面在变形后仍然垂直于中性面,即Kirchhoft假设;
(2)FGM圆板为小变形;
(3)FGM圆板的弹性模量及泊松比沿厚度方向按照体分比函数连续变化。
取FGM圆板的物理中面为hz=h0,则:

(4)
FGM圆板内任意一点的位移在r,θ,z方向上的位移分别为u,v,w。对于周边简支的FGM圆板,其半径为R,厚度为h,受到均布载荷q0,在平板上取单元体,如图2所示。
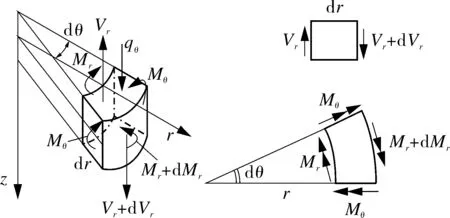
图2 FGM圆平板单元体
z方向所受的力的平衡方程为[17]:
-Vrrdθ+(Vr+dVr)(r+dr)dθ+q0rdrdθ=0
(5)
式中Vr——单位长度上的剪力,N;
q0——均布载荷,MPa。
根据微元体的力矩平衡条件,所有内力与外力对圆柱体外壁面切线的力矩代数和为零,即:
(6)
式中Mr——径向弯矩,N·m;
Mθ——周向弯矩,N·m。
根据前文假设在横截面上的切向应变γrθ,γθz及轴向应力σz均为0,可以得出下式:
(7)
式中σr——径向应力,MPa;
μ——泊松比;
εr——径向应变,mm;
εθ——周向应变,mm;
σθ——周向应力,MPa;
τrθ——切向应力,MPa;
γrθ——切向应变,mm。
(8)
式中r——任意一点处的半径,mm。
因弯矩Mr,Mθ是应力σr,σθ沿板厚方向的积分,建立弯矩Mr与Mθ与挠度w的关系如下:
(9)
对于轴对称FGM圆平板,利用弹性理论中的位移法即可建立可解的平衡方程。联立式(9)与式(6)可得:
(10)
联立式(5),式(10),可得周边简支的FGM圆板位移函数:
(11)

式(11)中有4个未知系数A,B,C,D,需补充如下边界条件。
(1)因r=0时lnr无意义,所以为满足w在r=0处存在,所以D=0。

将系数A,B,C,D代入式(11),求得周边简支的FGM圆板位移函数表达式:
(12)
将式(12)代入式(9)得到弯矩方程,求得周边简支的FGM圆板应力表达式为:
(13)
1.1.3 FGM管板应力分布计算公式
GB/T 151—2014《热交换器》中对管板计算的基本假设是把管板视为承受均布载荷、放置在弹性基础上的且受管孔均匀削弱的当量圆平板,当量圆平板应力分析的主要依据是弹性力学板壳理论中的Kirchhoff薄板理论。在计算中考虑管板的整体弯曲变形和面内拉伸变形,而忽略由于介质压力作用于管孔带上产生的局部变形,同时将管孔周边和管孔带上的应力集中按应力分类原则划分为峰值应力,在强度校核中不予考虑[18]。因此,针对U形管式换热器中法兰连接且不兼做法兰的功能梯度管板的应力分析中,首先对管板进行模型简化,简化后的力学模型见图3。

图3 管板简化力学模型
对a型管板来说,R即为垫片压紧力作用中心圆半径,Rt为布管区当量半径,pt为管程内压,ps为壳程内压。从图3中可知,简化后的a型管板相当于周边简支的当量圆平板,当量圆平板由一个不布管区的圆环与一个将布管区通过管孔削弱系数简化成的实心圆板组成。计算布管区域应力时,利用刚度削弱系数进行计算[19]。
由于梯度材料两个相的泊松比相差不大,可以认为泊松比为常量,不随坐标变化,令其为μ;令管板的设计压力为q0。并且管板简化后的力学模型中圆环和环内的圆盘弹性模量不同,结合式(11)可知,管板的位移函数是由两段函数构成的一个连续函数,即:
(14)
式中η——弯曲刚度系数;
Rt——管板布管区当量半径,mm。
位移函数除了满足前面的边界条件外,还应满足下面的变形协调方程:
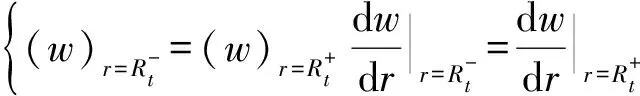
(15)
根据位移函数、边界条件及变形协调方程,求出管板的应力分布:
(16)
(17)
式中μ*——强度削弱系数。
由于简支约束在r=R处弯矩为0,因此可能存在应力最大值的点只剩下r=0和r=Rt处,两处应力值的计算方法如下。
当r=0时:
σr=σθ
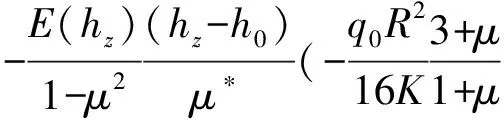
(18)
当r=Rt时:
(19)
1.2 功能梯度管板应力理论值计算
以某厂的冷却器功能梯度管板为研究对象,采用上述推导的理论计算公式进行计算,获取管板的理论计算应力值。该大型冷却器管板采用功能梯度材料制造,设计参数如表1所示。
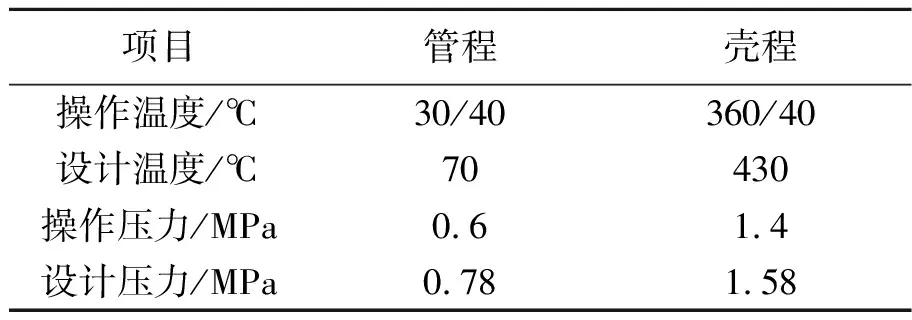
表1 管板设计参数
管板采用功能梯度材料制造,连接方式为a型连接方式,即管箱与壳体皆通过螺栓法兰垫片与管板进行连接,壳程侧采用耐高温且隔热性能良好的ZrO2陶瓷,管程侧为022Cr17Ni12Mo2不锈钢,中间采用梯度方式连续过渡,梯度因子β=1,管板厚度110 mm。
定义Orθ位于管程侧表面,O位于管板管程侧表面中心,从管程侧指向壳程侧方向为z轴正方向,计算均布载荷q0在管壳程压力共同作用时危险截面应力值。将相关参数带入式(1)中,得到管板的中性面位置h0=52.762 mm,计算系数K=1.898×1010。
根据ASME规范相应的计算得到刚度削弱系数η=0.471,强度削弱系数μ*=0.53,管板布管区当量半径Rt=448.6 mm。
在管壳程压力共同作用下,根据式(18),(19)计算危险点处的应力如下。
(1)在r=0处时。
σr=σθ
=-6.423×10-6×(193000-381.818z)
×(z-52.762)
经计算,在管程侧表面z=0处,σr=σθ=65.40 MPa;在壳程侧表面z=110处,σr=σθ=-55.51 MPa。
(2)在r=Rt处时。
σr=-1.279×10-6×(193000-381.818z)×(z-52.762)
σθ=-1.989×10-6×(193000-381.818z)×(z-52.762)
经计算,在管程侧表面z=0处,σr=13.02 MPa,σθ=20.25 MPa;在壳程侧表面z=110处,σr=-11.051 MPa,σθ=-16.76 MPa。
2 压力作用下功能梯度管板应力有限元分析
功能梯度材料的材料参数随位置变化的特性给其有限元模型带来了很大困难。文中选用ABAQUS、并利用ABAQUS的USDFLD子程序来进行功能梯度管板的建模及有限元分析,通过自定义场变量来控制材料属性设置,使材料属性成为空间域的函数,进而实现功能梯度材料有限元模型的建立,使其满足有限元分析要求[20]。根据第1.2节以及表2中参数,进行功能梯度材料管板与相关USDFLD子程序编写。

表2 FGM管板金属相与陶瓷相材料属性
首先进行FGM管板的几何建模,考虑管板的对称性,建立管板的1/4模型,根据圣维南定理,计算选取换热管外伸长度为100 mm,建立几何模型如图4所示。
在property模块中根据表2中数据定义材料属性,并在材料定义模块中添加场变量及用户自定义场变量选项。ABAQUS不能直接进行映射网格划分,只能通过Use mapped meshing where appropriate选项让程序自动判断。在可选的划分方式中,结构化网格的质量最高,后续计算也容易收敛。管板本身的模型复杂,不能采用结构化网格划分,但可以运用partition工具将管板沿着换热管孔切割,分成形状简单的区域,使其能够进行结构化网格划分。对管板进行合理切割,采用结构化网格进行划分,所得单元都是六面体单元,共划分的单元数量为601 662个,节点数量为721 463个。FGM管板的有限元模型如图5所示。
图4 FGM管板几何模型

图5 管板有限元模型
在第三强度理论下分析管壳层压力共同作用下FGM管板的等效应力、径向应力与周向应力。选择管板有限元模型的单元类型为C3D8,在step模块中选择静力分析模块,在load模块中施加载荷,在管板的管程侧和换热管内表面施加管程设计压力0.78 MPa,在壳程侧及换热管外表面施加壳程设计压力1.58 MPa,在管板的两个对称面施加对称约束,在管板与法兰的连接面上施加夹紧约束,在换热管的截面上施加换热管轴向力。进入job模块,加载编好的USDFLD子程序并进行求解。文中主要是进行管板应力分析,因此需要略去换热管,取管板为局部模型进行详细的应力分析。管板的第三强度理论应力云图见图6,可以看出,最大值位于管板中心开孔处,为68.56 MPa。

图6 第三强度理论管板等效应力云图
以全局坐标系为基础建立柱坐标系,查看管板的径向应力和周向应力,如图7,8所示。

图7 管板径向应力分布云图

图8 管板周向应力分布云图
从图中可以看出,管板的径向应力最大值与管板周向应力最大值均位于管板中心附近的开孔处。忽略计算误差,管板中心处的径向应力与周向应力相等,在管程侧的值为63.59 MPa,在壳程侧的值为-55.15 MPa。
3 FGM管板理论解与有限元解对比分析
第1节中求出了弹性理论下FGM管板在危险点处沿z轴(即厚度方向)的应力分布函数,并计算出在管程侧与壳程侧表面危险点处的应力值,根据第2节的有限元分析可以提取出危险点处沿厚度方向的应力分布的有限元解及管程侧与壳程侧表面危险点处应力的有限元解,其结果如表3所示。
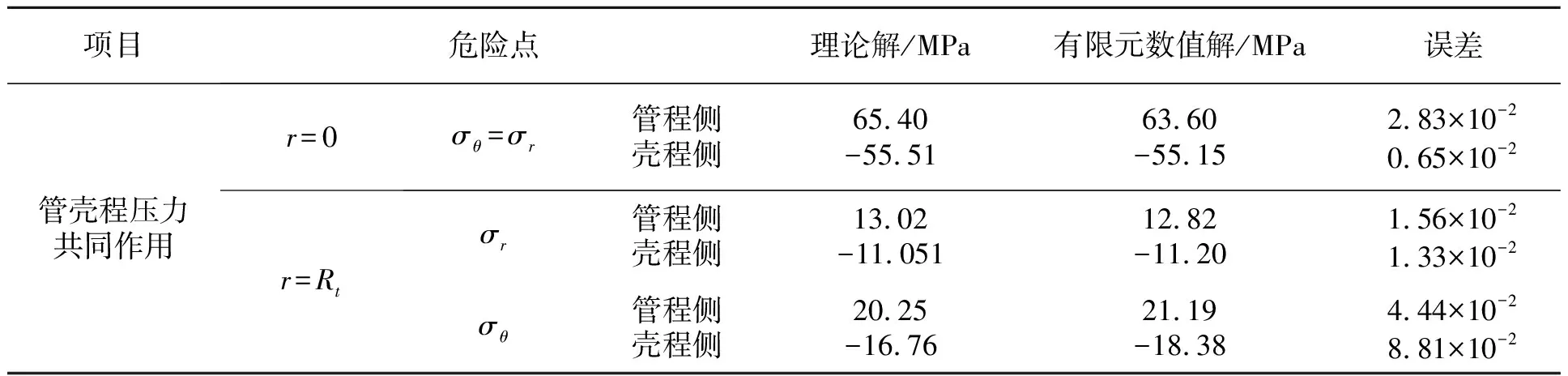
表3 管板危险点处应力
在r=0及r=Rt处分别列出管板沿厚度分布的径向应力及周向应力的理论解析解及有限元数值解曲线。考虑到开孔削弱及隔板槽的影响,在绘制有限元解曲线时选取最大值及最小值所在处的应力分布进行绘制。图9~11中h=0处为管程侧表面,h=110处为壳程侧表面。

图9 管壳程压力共同作用下管板中心r=0处径向应力及周向应力分布
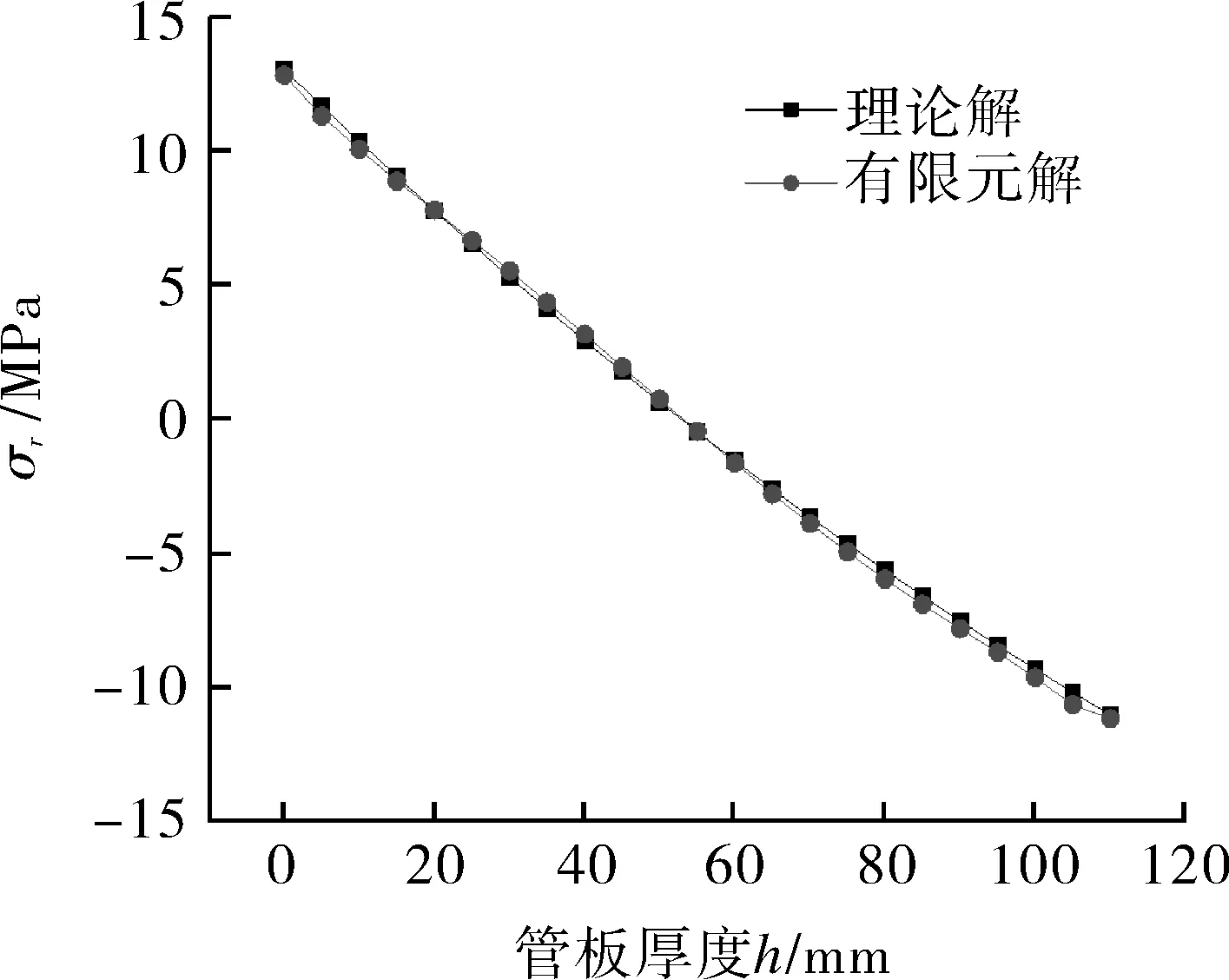
图10 管壳程压力共同作用下布管区边缘r=Rt处径向应力分布

图11 管壳程压力共同作用下布管区边缘r=Rt处周向应力分布
图9示出管壳程压力共同作用下FGM管板在r=0处的径向应力及周向应力沿管板厚度分布曲线的理论解与数值解对比图,可以看出,在管程侧表面应力值大于0,为拉应力,在壳程侧应力值小于0,为压应力,在管板的两侧表面分别取最大值和最小值。
图10为管壳程压力共同作用下FGM管板在r=Rt处的径向应力沿管板厚度分布的理论解与数值解曲线对比图,图11为管壳程压力共同作用下FGM管板在r=Rt处的径向应力沿管板厚度分布的理论解与数值解曲线对比图,可以看出,在管程侧表面应力值大于0,为拉应力,在壳程侧应力值小于0,为压应力,在管板的两侧表面分别取最大值和最小值。
分析图9,10可知,利用第1节中所推导的FGM管板应力分布计算公式所得到的理论解与有限元分析所获得的数值解曲线几乎重合;分析图11可知,在r=Rt处的周向应力曲线拟合差一些,但误差在允许范围内,充分说明了理论解的正确性。
4 结语
基于弹性理论,研究了功能梯度管板在压力载荷下的应力分布情况,并且推导了相关应力分布计算公式。之后,利用ABAQUS及其USDFLD子程序建立了功能梯度管板的有限元模型,对压力载荷下的功能梯度管板进行了静力分析,对比分析了理论解曲线与有限元解曲线的拟合效果,验证所推导应力分布计算公式的正确性,为功能梯度管板的设计校核提供了理论基础。文中虽然对功能梯度管进行了弹性理论解的推导及有限元数值分析,但由于受到客观条件的限制,笔者仅仅给出了静力载荷下的功能梯度管板的弹性理论应力计算公式,后续可以继续研究弹性理论下的热应力理论解及热力耦合载荷下的应力分布。

