An Efficient Outlier Detection Approach on Weighted Data Stream Based on Minimal Rare Pattern Mining

Saihua Cai,Ruizhi Sun,2,＊,Shangbo Hao,Sicong Li,Gang Yuan

1 College of Information and Electrical Engineering,China Agricultural University,Beijing 100083,China

2 Scientific Research Base for Integrated Technologies of Precision Agriculture (Animal Husbandry),the Ministry of Agriculture,Beijing 100083,China

Abstract: The distance-based outlier detection method detects the implied outliers by calculating the distance of the points in the dataset,but the computational complexity is particularly high when processing multidimensional datasets.In addition,the traditional outlier detection method does not consider the frequency of subsets occurrence,thus,the detected outliers do not fit the definition of outliers (i.e.,rarely appearing).The pattern mining-based outlier detection approaches have solved this problem,but the importance of each pattern is not taken into account in outlier detection process,so the detected outliers cannot truly reflect some actual situation.Aimed at these problems,a two-phase minimal weighted rare pattern mining-based outlier detection approach,called MWRPM-Outlier,is proposed to effectively detect outliers on the weight data stream.In particular,a method called MWRPM is proposed in the pattern mining phase to fast mine the minimal weighted rare patterns,and then two deviation factors are defined in outlier detection phase to measure the abnormal degree of each transaction on the weight data stream.Experimental results show that the proposed MWRPM-Outlier approach has excellent performance in outlier detection and MWRPM approach outperforms in weighted rare pattern mining.

Keywords: outlier detection; weighted data stream; minimal weighted rare pattern mining; deviation factors

I.INTRODUCTION

Data stream is a special form of data,which has the characteristics of continues,unbounded and not necessarily uniformly distributed.Because the data stream can truly reflect the changing characteristics of the monitored things,it is widely present in the sensor network [1].However,outliers are often accompanied by the data stream,which seriously affect the accuracy of data-based predictions,where outliers are rarely appearing and are significantly differing from most other data [2].Thus,there is a critical necessary to discover the outliers so as to improve the reliability of the data.

The traditional outlier detection approaches are roughly divided into the following: (1)cluster-based approaches [3,4],(2)distance-based approaches [5,6],(3)density-based approaches [7,8] and (4)pattern mining-based approaches [9-11].It can be known from the definition of outliers that the appearing frequency of the contained patterns is a key factor in outlier detection.However,previous three approaches (cluster-based,distance-based and density-based)did not take the frequency of each pattern into account in the outlier detection process,thus,the detected outliers have a certain deviation from the definition of the outliers.The pattern mining-based approaches have resolved this problem well,and the detection efficiency was also improved.The main process of pattern mining-based outlier detection approach is divided into the following two phases: (1)mining rarely appearing patterns or frequently appearing patterns,and (2)detecting the implicit outliers based on the mined patterns.

Compared with the frequent pattern mining-based outlier detection approaches,the rare pattern mining-based approaches provide support for outlier detection by mining the rare patterns (the pattern'ssupportvalue is less than a predefined minimal thresholdmin_sup),which is more consistent with the characteristics that are rarely appearing in the definition of outliers.As a result,the outlier detection is more accurate.However,the following two limitations always affect the results of rare pattern mining.First,the scale of data stream in real life is very large,it will consume a lot of time to mine the rare patterns by scanning data stream multiple times (e.g.Apriori-based methods)or by generating a large number of conditional trees (e.g.FP-Growth-based methods).And the large scale of the mined rare patterns will also increase the time consumption of the outlier detection phase substantially.Second,not all patterns are equally important (for example,the goods in the shopping cart have different values),but the previous methods only considered the times of patterns that occurred and ignored the weight (importance)of each pattern,so the important patterns that occurred less frequently could be ignored during the pattern mining process.Similarly,in the outlier detection phase,the weight value of each pattern will also affect the effect of outlier detection.Therefore,the previous outlier detection approaches are not applicable to weighted data stream.

Driven by the aforementioned challenging issues,this paper first proposes a Minimal Weighted Rare Pattern Mining approach called MWRPM,which is used to efficiently mine the minimal weighted rare patterns (MWRPs)from the weighted data stream.Here,the mining objects areMWRPsrather than weighted rare patterns because theMWRPsare the generator of all weighted rare patterns.Thus,the number of mined patterns is much less,which will increase the efficiency of outlier detection phase.Then,this paper proposes an efficient Minimal Weighted Rare Pattern Mining-based Outlier detection approach,called MWRPM-Outlier,to discover the implicit outliers on the weighted data stream.The approach proposed by us fully considers the weight value of each pattern,so the detected outliers are closer to some practical applications.The main contributions of this paper can be summarized as follows:

(1)We propose a new approach called MWRPM to effectively mine theMWRPsfrom weighted data stream (to our best knowledge,it is the first algorithm aims at miningMWRPsfrom weighted data stream).Specific,the matrix structure is constructed to store the information of weighted data stream,and then theMWRPsare mined with the “pattern extension” operation from the weighted frequent 1-patterns to weighted frequent longer-patterns.

(2)We design two deviation factors (Minimal Weighted Rare Pattern Deviation Factor(MWRPDF)and Transaction Deviation Factor (TDF)to measure the abnormal degree of each transaction,and then propose the MWRPM-Outlier approach to effectively detect the implicit outliers in the weighted data stream.

(3)We conduct extensive performance analysis on two public datasets and a synthetic dataset to evaluate the efficiency of the proposed approaches,and the experimental results show the validity and accuracy of the proposed methods.

The remainder of this paper is organized as follows.The related work is presented in Section 2.The preliminaries and problems are introduced in Section 3.The minimal weighted rare pattern mining approach and outlier detection approach are presented in Section 4.The empirical studies and experimental analysis are stated in Section 5.Finally,the conclusions and future work are discussed in Section 6.

II.RELATED WORK

In this section,some related work is illustrated on three aspects: (1)outlier detection approaches; (2)rare pattern mining approaches; and (3)weighted frequent pattern mining approaches.

2.1 Outlier detection approaches

In recent years,several outlier detection approaches have been proposed to effectively detect the implicit outliers,such as distance-based approaches,density-based approaches and pattern mining-based approaches.

To eliminate the limitations of the previous algorithms,Kontaki et al.[5] proposed three efficient algorithms for continuously monitoring the distance-based outliers using sliding window technology.The outlier detection operation is performed by flexibly adjusting the radius parameterRand the threshold parameterk.Specifically,the algorithm COD [5] could flexibly process multiple threshold parameterkunder the fixed radius parameterR,and its outlier detection time consumption is relatively low.Then,they proposed an improved version called ACOD [5],which could process the distance-based outlier detection operation in the case of changing radius parameterRand changing threshold parameterk.To further reduce the computation of distance,they proposed a micro-cluster-based algorithm MCOD [5] to support multiple queries to maintain a small amount of distance computation.Cao et al.[6] proposed two novel optimization principles,namely “minimal probing” and “lifespan-aware prioritization”,to achieve scalable outlier detection operations,and then they designed a general framework called LEAP to process three major classes of distance-based outliers in stream environments,where the traditional distance-based outlier detection and the nearest-neighbor-based outlier detection were integrated in the framework.Based on the local kernel density estimation,an efficient density-based outlier detection approach called RDOS [8] was proposed by considering theknearest neighbors,the reverse nearest neighbors and the shared nearest neighbors.

For the pattern mining-based outlier detection approaches,the FindFPOF [9] algorithm used the ratio of thesupportvalue of the contained frequent patterns to the total number of frequent patterns as a judgment condition to detect the outliers in the datasets.However,the large-scale frequent patterns resulted very expensive time cost in outlier detection phase.To solve this problem,the maximal frequent patterns [11,12] were used to replace the frequent patterns to reduce the number of patterns.In 2014,the minimal infrequent pattern mining-based outlier detection method called MIFPOD [10] was first proposed to discover the implicit outliers,which used the transaction weighting factor (TWF),minimal infrequent deviation factor (MIPDF)and minimal infrequent pattern-based outlier factor (MIFPOF)to measure the abnormal degree of each transaction.

2.2 Rare pattern mining approaches

Rare pattern mining was an important branch of data mining,and it was designed to mine the rare patterns whosesupportvalue is less than predefined minimalsupportthresholdmin_sup.Until now,several algorithms [13-16] have been proposed to effectively mine the rare patterns,which could be divided into Apriori-like approaches and FP-Growth-like approaches.

For the Apriori-like approaches,an efficient high utility rare itemset mining (HURI)algorithm [13] was proposed to mine the rare itemsets with high utility,and the whole process was divided into two phases.In the first phase,the inverse Apriori concept was used in HURI to mine the rare itemsets with thesupportvalue less than predefined maximalsupportthreshold based on the users' interests.In the second phase,the pruning operation was carried out according to the utility value in the process of mining rare patterns.The purpose is to mine efficient rare patterns whose utility values are not less than the predefined minimal utility threshold more quickly.To mine the infrequent associations,the exclusion mechanism [14] was introduced to reduce the impact of the frequent patterns on the mining process,and then a new measurement factor was proposed based on the decision model caused by fuzzy recognition.In addition,an effective data mining approach was developed to mine the infrequent causal associations,which was used to analyze the relationship between the drug and its corresponding adverse drug.

For the FP-Growth-like approaches,Tsang et al.[15] proposed an algorithm called RPTree [15] to mine the rare patterns,where three ideas were used to improve the mining efficiency of the existing methods.The three ideas could be summarized as follows: (1)using a tree structure similar to FP-Tree to avoid expensive “extension” process and pruning process; (2)designing the RP-Tree to mine rare patterns other than frequent patterns; (3)dividing the pattern search space into multiple blocks and the mining operation was conducted in each block.In 2014,Cagliero and Garza proposed the IWI-Miner algorithm [16] and MIWI-Miner algorithm [16] to mine the rare itemsets,where IWI-Miner was used to discover the rare itemsets with different weight values and MIWI-Miner was used to discover the minimal infrequent itemsets with different weight values.

2.3 Weighted frequent pattern mining approaches

In the weighted frequent pattern mining approaches,the different importance of each pattern was taken into account,thus,the mined frequent patterns are more important.In recent years,several weighted frequent pattern mining approaches [17-20] have been proposed to quickly and effectively mine the weighted frequent patterns.

Yun et al.proposed the weighted frequent itemset mining algorithm called WFIM [17] to mine more efficient patterns by considering both thesupportvalues and the weight values.It first defined the weight range and the minimal weight value,and then the weight andsupportof each pattern were considered separately to prune the search spaces.Based on the WFIM approach,the scale of mined patterns was reduced a lot compared with the frequent pattern mining approaches.In order to improve the mining efficiency of Apriori-like approaches,a novel tree structure based on weight ascending order called IWFPTWA[18] was constructed to store the item information and its frequency,and then the IWFPWAalgorithm [18] was proposed to mine the weighted frequent itemsets by obtaining the highest weighted item at the bottom of the IWFPTWA.However,many non-candidate items may appear with the candidate items because the weight ascending order does not guarantee that the candidate items will appear before the non-candidate items,which would increase the creation time of the prefix trees and conditional trees during the mining operation.To solve this problem,a new tree structure called IWFPTFDwas constructed based on the frequency descending order,and this highly compact incremental tree structure can speed up the mining efficiency.Then,the WIT-FWI algorithm [19],WIT-FWI-MODIFY algorithm [19] and WIT-FWI-DIFF algorithm [19] were proposed continuously to mine the weighted frequent patterns.

Table I shows the characteristics of the aforementioned rare pattern mining algorithms and weighted frequent pattern mining algorithms.Each column of Table 1 is the considered factor that the algorithm supports,such as: streaming,weight,or minimal rare.Note that our proposed algorithm is compared to the state-of-the-art approaches,IWFPWA,IWFPFD,WIT-FWI,WIT-FWI-MODIFY and WITFWI-DIFF.

III.PRELIMINARIES AND PROBLEMS

In this section,we first introduce the preliminaries related to this paper and then list some existing problems in outlier detection operations on weighted data stream.

3.1 Preliminaries

PatternP={p1,p2,…,pn} is a set of items,andPs={p1,p2,,…,pk} is ak-pattern (kis the length ofPs),wherePs⊆Pandk∈[1,n].Psis called a subset ofP,andPis called the superset ofPs.Data streamDS=[T1,T2,…,Tm)contains a collection of infinite transactions with a identifierTID,whereTiis a subset ofP.Weight tablewtable={w(p1),w(p2),…,w(pn)} records the weight value of each pattern {pj}.To process the most recent transactions in data stream,the sliding window (SW)model is often used in data stream environment,where the |SW| is the size of sliding window.The minimal weightedsupportthreshold (denoted asmin_wsup)of the sliding window is given to judge whether the mined patterns are rare or not.

Table II shows a weighted data stream,it is used to illustrate the definitions more intuitively,themin_wsupvalue in this example is 1.8 and the |SW| is 6.

Definition 1.Transaction weight(tw): Thetransactionweightof each transactionTjin current sliding window is denoted astw(Tj),and it is defined as:

where |Tj| is the contained number of pattern {pj} in transactionTj.

In the example of Table II,thetransactionweightofT1istw(T1)=(0.2+0.7+1+0.4)/4 =0.575,and the specifictwvalue of each transaction is shown in Table III.

Definition 2.Expectweightsupport(expwsup): Theexpect weight supportof pattern {X} in the current sliding window is denoted asexpwsup(X),and it is defined as:

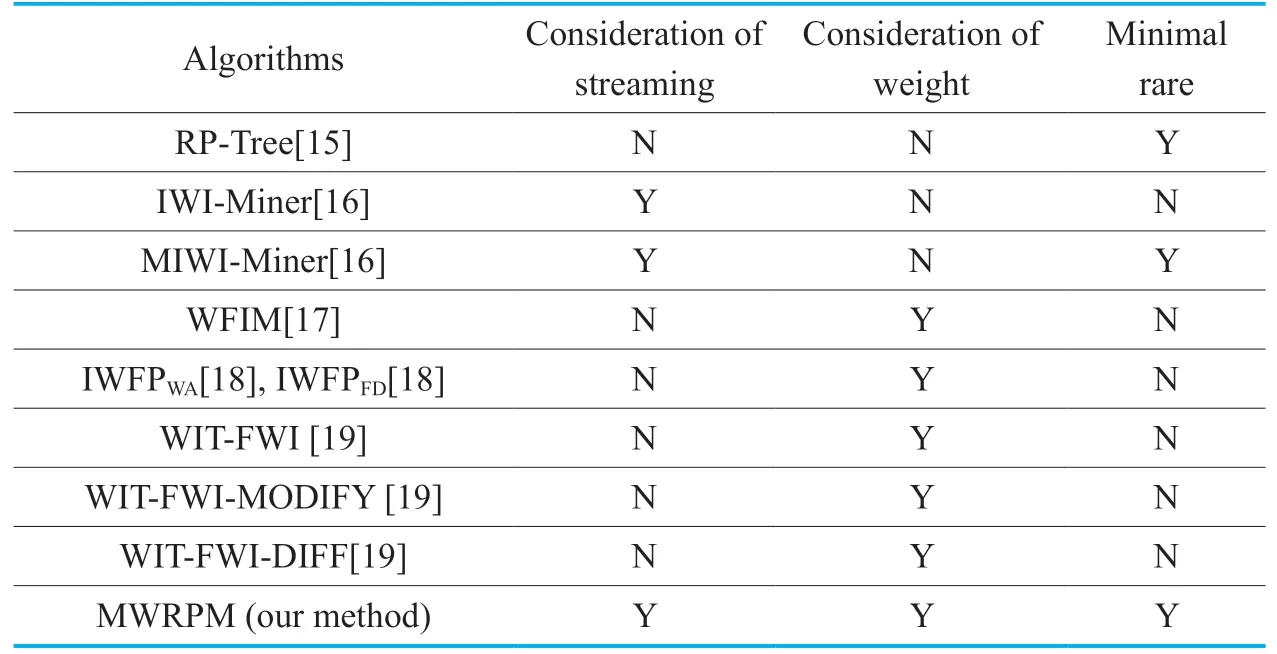
Table I.Characteristics of pattern mining algorithms.

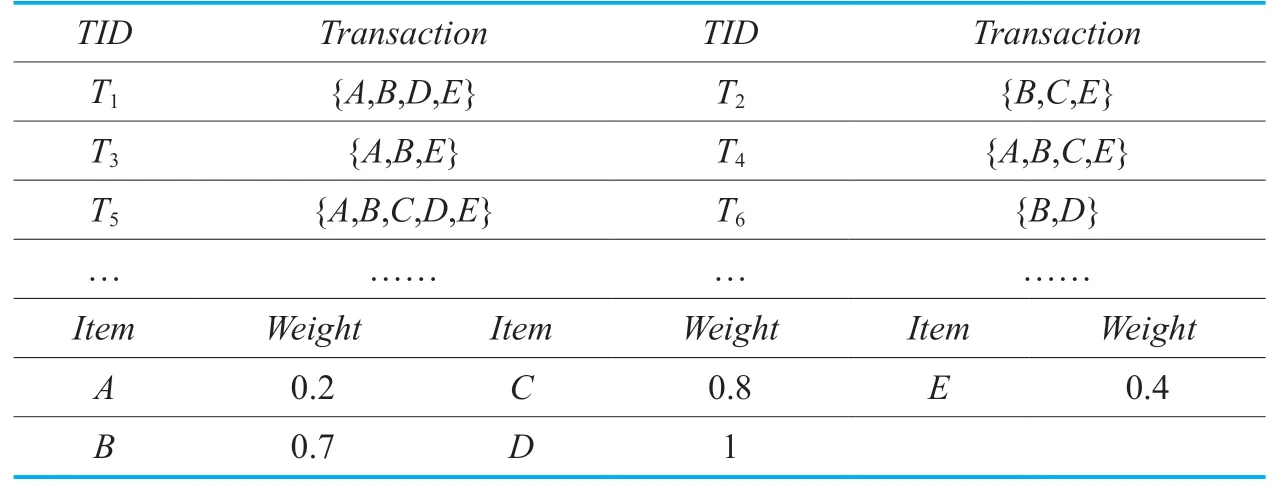
Table II.An example of weighted data stream.

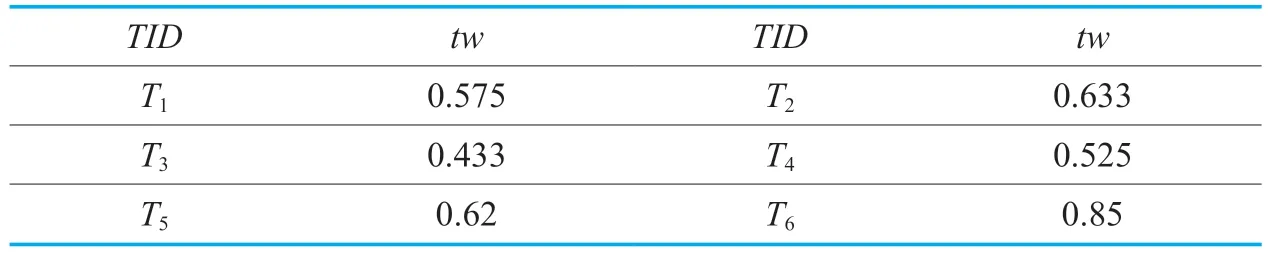
Table III.The tw value of each transaction.

In the example of Table II,theexpect weight supportof pattern {A} in the current sliding window isexpwsup(A)= (0.575+0.433+0.525+0.62)=2.153,and theexpect weight supportof pattern {AD} in the current sliding window isexpwsup(AD)=(0.575+0.62)=1.195.

Definition 3.Weighted Rare Pattern (WRP): Pattern {X} is a weighted rare pattern if itsexpwsupvalue is less than the predefinedmin_wsup,that isexpwsup(X)＜min_wsup.

In the example of Table II,expwsup(C)=1.778＜1.8,thus,pattern {C} is a weighted rare pattern.

Definition 4.Weighted Frequent Pattern (WFP): Pattern {X} is a weighted frequent pattern in current sliding window if itsexpwsupvalue is not less than the predefinedmin_wsup,that is:expwsup(X)≥min_wsup.

In the example of Table II,becauseexpwsup(B)= 3.636＞1.8,thus,pattern {B} is a weighted frequent pattern.

Definition 5.Minimal Weighted Rare Pattern (MWRP): Pattern {X} is a minimal weighted rare pattern if {X} is aWRPand no subset of {X} is weighted rare.

In the example of Table II,pattern {C} is a minimal weighted rare pattern becauseexpwsup(C)=1.778＜1.8 and no subset of pattern {C} is weighted rare.Pattern {AC}is not a minimal weighted rare pattern because its subset {C} is weighted rare.

3.2 Problems description

In this subsection,the problems of minimal weighted rare pattern mining and outlier detection on weighted data stream are listed as follows.

3.2.1 Problem of Minimal Weighted Rare Pattern Mining

The weight information of each pattern will affect the final result of determining whether the mined patterns are frequent patterns or not,but the traditional frequent pattern mining approaches or rare pattern mining approaches do not use the weight value of each pattern as a criterion for pattern mining,the weighted pattern mining has gradually become a challenging issue.However,to our best knowledge,there is no minimal weighted rare pattern mining approach has been proposed for weighted data stream until now.

3.2.2 Problem of Outlier Detection on Weighted Data Stream

As can be known from Hawkin's definition of outlier,the appearing frequency of each pattern is a key factor in outlier detection.However,the distance-based outlier detection approaches and density-based outlier detection approaches have not used the frequency of each pattern as a detection criterion,so there are some discrepancies between the detected outliers and the definition of outliers.In addition,for the existing frequent pattern mining-based outlier detection approach,such as FindFPOF [9],the deviation factors used in the outlier detection process is very simple,which will result the accuracy of outlier detection is not very high.Besides that,the large scale of mined frequent patterns will cause the outlier detection phase to consume a relatively long time.However,to our best knowledge,there is still no pattern mining-based outlier detection approach has been proposed for weighted data stream until now.

IV.OUTLIER DETECTION ON WEIGHTED DATA STREAM

For the weighed data stream,we first propose a minimal weighted rare pattern mining method called MWRPM to quickly mine theMWRsfrom the weighted data stream,and then propose an outlier detection approach called MWRPM-Outlier to detect the abnormal transactions from the weighted data stream.

4.1 Overall framework of outlier detection

Similar to the frequent pattern mining-based outlier detection approaches,the minimal weighted rare pattern mining-based outlier detection approach can be divided into the following two phases: (1)minimal weighted rare pattern mining phase; and (2)outlier detection phase.The purpose of minimal weighted rare pattern mining phase is to mine the minimal weighted patterns (MWPs)from the weighted data stream,thus providing a pattern basis for the outlier detection phase.The purpose of outlier detection phase is to discover the implicit outliers from the weighted data stream based on the minedMWRsand designed deviation factors.The overall framework of the outlier detection process is shown in figure 1.

When the weighted data stream reaches the computer terminal,it automatically enters the pattern mining module.In this module,the data information andtwvalue of each pattern are stored in the matrix structure,and then the “pattern extension” operation is conducted to mine theMWRsfrom weighted data stream.After allMWRsare mined from the weighted data stream,the outlier detection process is carried out using the deviation factors and minedMWRsto discover the implicit outliers.

4.2 Minimal weighted rare pattern mining approach

The major task of this subsection is to introduce the main idea of the proposed minimal weighted rare pattern mining (MWRPM)approach.

4.2.1 The Main Idea of MWRPM Approach

For the Apriori-based methods,the entire dataset needs to be scanned multiple times to determine whether the extended patterns are frequent,and for the FP-Growth-based methods,a large number of conditional trees need to be built to recursively mine the frequent patterns,so they are time consuming.However,for the dense datasets,the subsets and their supersets are more likely to appear in the same transactions,so many calculations ofexpwsupvalues are not necessary.To quickly know which transactions a pattern is included in,the information of each pattern needs to stored.Thus,we built a matrix structure to store thetwvalues for each pattern,which avoid multiple scans of the entire weight data stream to reduce the time consumption.

The construction process of the matrix A is very simple.If pattern {pi} exists in transactionTd,thetwvalue is written to the position ofAdi,otherwise,the position ofAdiis written in 0.When the information of all transactions in the current sliding window are stored into matrix A,thetwvalue of each pattern is added and written to the last row of matrix A.Then,we use the pattern information in Table II as an example to show the specific construction process of matrix A.When transactionT1flows into the sliding window,the columns are constructed in turn for patterns {A},{B},{D} and {E},and thetw(T1)is written toA11,A12,A13andA14in turn,the constructed matrix A is shown in figure 2(a).When transactionT2flows into the sliding window,the column for pattern {C} need to be created because pattern {C} is not inT1,and then thetw(T2)is also written to the corresponding positions,the constructed matrix A is shown in figure 2(b).Follow the above steps until the information of all transactions is stored in matrix A,and then thetwvalue of each pattern is added and written to the last row of matrix A,the constructed matrix A is shown in figure 2(c).

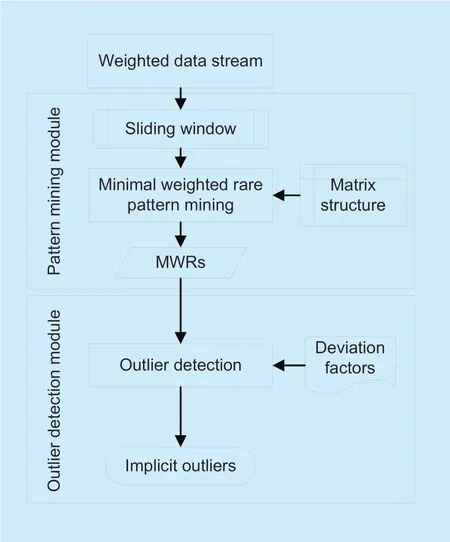
Fig.1.Overall framework of outlier detection process.

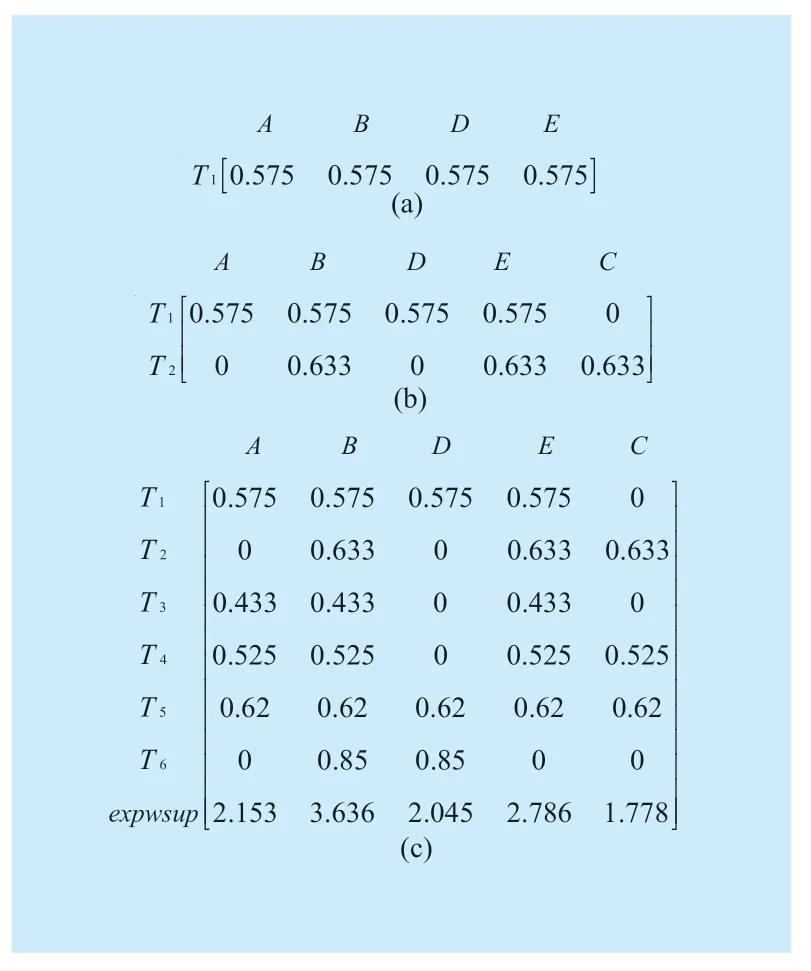
Fig.2.The construction of matrix A.

After the matrix A is constructed,the 1-patterns whoseexpwsupvalue is less than the predefinedmin_wsupare stored in the Minimal Weighted Rare Pattern Library MWRP-L.Then,those weighted frequent 1-patterns are the potential patterns for the subsequent “pattern extension” operations.

In 2013,Vo et al.[19] proposed an efficient WIT-FWI-DIFF algorithm to mine theWFPsfrom the dense datasets.Because in the dense datasets,the number of subsets and supersets appearing in different transactions is much smaller than that appearing in the same transactions,thus,the WIT-FWI-DIFF method can significantly reduce the time cost of theexpwsupvalue calculation.However,the mined object of the WIT-FWI-DIFF method is the weighted frequent patterns,therefore,we adjust some steps of the WIT-FWI-DIFF and propose a minimal weighted rare pattern mining method called MWRPM to effective mine theMWRPsfrom weighted data stream.

Assume the differentTIDsbetween patterns {PX} and {PY} isDif(PXY),then it can be known from literature 20 thatDif(PXY)=TPXTPY=Dif(PY)Dif(PX).Due to pattern {PXY} is extended by patterns {PX} and {PY},that is:

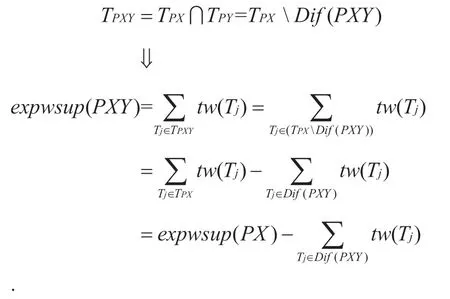
The above inference shows that ifDif(PXY)=Φ,then,expwsup(PXY)=expwsup(PX).

Based on the above analysis,the main time consumption of the minimal weighted rare pattern mining phase is the calculation ofexpwsupvalues,so the time cost of the pattern mining phase will be reduced if the number of calculations can be reduced.For the weighted frequent 1-patterns,there is a large gap in the frequency of their appearance.If they are arranged in ascending order in the frequency of their appearance in the sliding window,theDifvalue of the extended pattern will be more likely to be empty,that is,theexpwsupvalue of the extended patterns no longer need to be calculated.In particular,if the appearing frequencies of the patterns are same in the sliding window,they are arranged in ascending order according to theirexpwsupvalues.For weighted frequentn-patterns {PX} and {PY},if patterns {PX} and {PY} have the same prefix (the front (n-1)items are same),they can be extended to (n+1)-pattern {PXY}.After obtaining the extended patterns,if the extended pattern is the superset of minedMWRPs,it needs to be deleted directly without further calculation,otherwise,theDifvalue of the extended pattern {PXY} is searched first.If theDifvalue of pattern {PXY} is empty,theexpwsupvalue of {PXY} is equal to theexpwsupvalue of {PX}; And if theDifvalue of pattern {PXY} is not empty,theexpwsupvalue of the extended pattern {PXY} is calculated.If theexpwsupvalue of the extended pattern is less than the predefinedmin_wsupvalue,each pattern in the MWRP-L is used to determine whether it is a subset of the extended patterns,if there is no subset of the extended patterns in MWRP-L,the extended patterns are added to MWRP-L.Repeat the above steps until all minimal weighted rare patterns in the current sliding window are mined.Then,the sliding window is sliding backward to mine theMWRPsfor the next stage.The detailed process of MWRPM method is shown in algorithm 1.

4.2.2 An example of MWRPM approach

To explain the proposed MWRPM approach more clearly,we use the example presented in Table II as an example,themin_wsupin this example is 1.8.

Step 1.The transactions in current sliding window are scanned first,and thetwvalue andexpwsupvalue of each pattern are written in matrix A in turn.The specific construction of matrix A is shown in figure 2.

Step 2.For pattern {C},becauseexpwsup(C)=1.778＜1.8,it is a minimal weighted rare pattern and stored into MWRP-L,then any “pattern extension” operation is no longer performed on pattern {C}.

Step 3.For the weighted frequent 1-patterns {A},{B},{D} and {E},they are arranged by their decrease appearing frequency.Due to pattern {A} is existingT1,T3,T4andT5,therefore,the appearing frequency of {A} is 4.Similar,the appearing frequencies of {B},{D} and {E} are 6,3 and 5.Therefore,the order of the “pattern extension” of the weighted frequent 1-patterns is adjusted into {D}→{A}→{E}→{B}.

Step 4.For the weighted frequent 1-patterns {D},{A},{E} and {B},they can be extended into 2-patterns {DA},{DE},{DB},{AE},{AB} and {EB},and then theexpwsupvalue of each extended pattern is calculated.

For pattern {DA}:

Thus,{DA} and {DE} are minimal weighted rare patterns,they are stored into MWRP-L.

Step 5.For the weighted frequent 2-patterns {DB},{AE},{AB} and {EB},because the 2-patterns with the same prefix are {AE} and {AB},thus,they can be extended into {AEB}.Then,the patterns in MWRP-L are used to check whether there is any subset of pattern {AEB}.Due to {AEB} is not the superset of anyMWRP,theexpwsupvalue is calculated to determine whether it is a minimal weighted rare pattern or not.

Algorithm 1.MWRPM.Input: Weighted data stream,n (size of |SW|),min_wsup Output: MWRPs 01.for |SW|≤n do 02.calculate tw value for each transaction 03.if {pk} in Td then 04.Ad,k=tw value of Td 05.else 06.Ad,k=007.end if 08.end for 09.calculate expwsup value of {pk}10.foreach expwsup(pk)＜min_wsup do 11.MWRP-L←{pk} // add the minimal weighted rare 1-pattern {pk} into MWRP-L 12.end for 13.foreach weighted frequent 1-pattern {px} and {py} do 14.extend {px} and {py} into {pxy}15.calculate expwsup(pxy)16.if expwsup(pxy)＜min_wsup then 17.MWRP-L←{pxy}18.end if 19.end for 20.x=221.foreach weighted frequent x-patterns {p1,…,px-1,pi} and {p1,…,px-1,pj} do 22.extend them into {p1,…,px-1,pi,pj}23.if any MWRP⊂{p1,…,px-1,pi,pj} then 24.delete {p1,…,px-1,pi,pj}25.else 26.calculate expwsup(p1,…,px-1,pi,pj)27.if expwsup(p1,…,px-1,pi,pj)＜min_wsup then 28.MWRP-L←{p1,…,px-1,pi,pj}29.end if 30.end if 31.end for 32.x++33.return MWRPs 34.slide the sliding window 35.go to 01

For pattern {AEB}:

Dif(AEB)=TAETAB=(1,3,4,5)(1,2,3,4,5)=∅,expwsup(AEB)=expwsup(AE)=2.153＞1.8.

Step 6.Because there are no longer patterns that can be extended,the mining process is ended.Therefore,the minedMWRPsare {C},{DA} and {DE}.

4.3 Outlier detection approach

The distance-based outlier detection method detects the implied outliers by calculating the distance of the points in the dataset,but it is not a choice for detecting the outliers on high-dimensional spatial data stream because of its high computational complexity in processing multi-dimensional datasets.The pattern mining-based outlier detection approach provides a good solution for outlier detection,in which the detected outliers are more consistent with the outliers defined by Hawkins.

In the pattern mining-based outlier detection approaches,a transaction is judged as an outlier if it deviates much from most other transactions,thus,the design of deviation factors are the key factors in outlier detection.For the FindFPOF method,it used the ratio of the support value of the contained frequent patterns to the total number of frequent patterns as a judgment condition,but the simple metrics make the accuracy of outlier detection not high.To solve this problem,we first define three deviation factors based on the mined minimal weighted rare patterns,which mainly improves the accuracy of outlier detection by considering more factors that will affect the judgment of outlier detection.

For the mined minimal weighted rare pattern (MWRP){X},the shorter of its length indicates it can be extended to more weighted rare patterns.In addition,the lowersupportof pattern {X} indicates the appearing frequency is fewer,thus,it is more abnormal than other patterns.Thus,the length andsupportof theMWRPare two factors that will affect the outlier detection,and then we design the Minimal Weighted Rare Pattern Deviation Factor calledMWRPDFbased on the minedMWRPs.

Definition 6.MWRPDF: For eachMWRP{X},theexpect weightsupportof {X} isexpwsup(X)and the length of {X} islength(X).TheMWRPDFof {X} is defined as

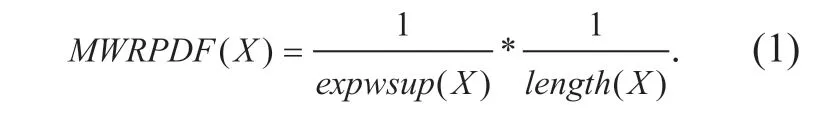
For each transactionTi,the smallerMWRPDFvalue of theMWRPsit contains indicates that more patterns inTiare frequent patterns,that is,the likelihood thatTiis an outlier is lower.In addition,if theMWRPDFvalue of theMWRPsin transactionT1and transactionT2are the same,but the length of isT1(length(T1))longer thanT2(length(T2)),which indicates that outlier density ofT2is greater thanT1,so transactionT2is more likely to be an outlier.Thus,the value of theMWRPscontained in transaction and the length of each transaction are two factors that will affect the outlier detection,and then we design the Transaction Deviation Factor calledTDFto measure the final deviation degree of each transaction in the weighted data stream.

Definition 7.TDF: LetDS=[T1,T2,…,Tn)bentransactions in the current sliding window,the length of transactionTiislength(Ti).TheTDFof transactionTiis defined as

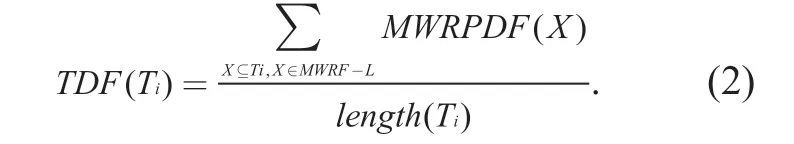
After calculating theTDFvalue for each transaction,the transactions are sorted using descendingTDFvalues.Because the possibility of a transaction being an outlier is positively correlated with theTDFvalue,thus,the topktransactions with largeTDFvalue are more like the outliers,valuekis usually specified by the users.Then,based on the designed deviation factors and minedMWRPs,we propose an outlier detection approach called MWRPM-Outlier to detect the implicit outliers on the weighted data stream.The detailed process of the MWRPM-Outlier approach is shown in algorithm 2.

4.3.1 An Example of MWRPM-Outlier Approach

The main process of MWRPM-Outlier approach is to judge the deviation degree of each transaction,where the calculation ofMWRPDFvalue andTDFvalue are the most important parts.To illustrate the proposed MWRPM-Outlier approach more clearly,we take the data information shown in Table II as an example,where the minedMWRPsare {C},{DA} and {DE}.

Step 1.TheMWRPDFvalue of each minedMWRPis calculated according to definition 6,and the specific process is shown as follows.

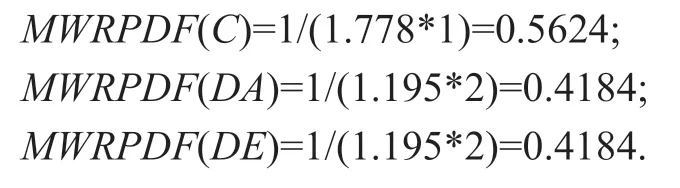
Step 2.TheTDFvalue of each transaction is calculated according to definition 7,and the specific process is shown as follows.

Step 3.After the calculation ofTDFvalues,the transactions are sorted using decreasingTDFvalues (T5→T1→T2→T4→T3→T6).Therefore,the possibility that the transaction is the final outlier,from large to small,isT5＞T1＞T2＞T4＞T3=T6.

V.EXPERIMENTS AND ANALYSIS

To test the accuracy of the outlier detection of the proposed MWRP-Outlier approach,massive experiments are carried out on a synthetic dataset based on different sizes of sliding window and differentmin_wsupvalues.Then,we use the datasetsmushroomandchessthat download from Frequent Itemset Mining Implementations Repository (http://fimi.cs.helsinki.fi/data/)to evaluate the mining efficiency of our proposed MWRPM approach,where the characteristics of the used datasets are shown in Table IV.In order to show the results of outlier detection preliminarily,the scale of synthetic dataset of this experiment is 600.The length of synthetic dataset is randomly selected from [5,9],and the weight value of each pattern is randomly assigned from (0,1].Then,we randomly implant several abnormal values into the generated synthetic dataset,and the transactions with abnormal values are marked.

In the experiments,in order to test the accuracy of outlier detection,the FindFPOF approach [9],MIFPOD approach [10],OODFP approach [12] and Thresh_LEAP approach [6] are used to compare with the proposed MWRPM-Outlier approach.Then,the pattern mining-based outlier detection approaches,FindFPOF OODFP and MIFPOD,are used as the comparison method to test the time efficiency of the MWRPM-Outlier approach.In addition,to evaluate the mining efficiency of the proposed MWRPM approach,the IWFPWA[18],IWFPFD[18],WIT-FWI [19],WIT-FWI-MODIFY [19] and WIT-FWI-DIFF [19] methods are used as the comparison methods.

All experiments are performed from a PC with 2.93 GHz CPU,4GB RAM,and Windows 10 OS.All of the algorithms in this paper are implemented in the python 3.6.

5.1 The detection accuracy of the MWRPM-Outlier approach

Algorithm 2.MWRPM-Outlier.Input: Data stream,n (maximal row of |SW|),k Output: Outliers 01.call Algorithm 102.MWRPDF(X)=0,TDF(Ti)=003.for X∈MWRP-L do 04.MWRPDF(X)=1/(expwsup(X)*length(X))05.end for 06.for i n∈ -[1,1] do 07.if X T X MWRP L⊆ ∈i,- then 08.TDF T MWRPDF X length T()()/ ()=∑09.end if 10.sort the transactions using dreasing TDF values 11.Outliers←top k Ti 12.end for i i

Table IV.Characteristics of datasets.

The outlier detection accuracy of the MWRPM-Outlier approach is carried out in differentmin_wsupvalues and different sizes of sliding window,where the size of sliding window is selected from 20,30 and 50,and themin_wsupvalue is selected as 30%,40% and 50% of the size of sliding window respectively.The accuracy of the outlier detection results are shown in figure 3 to figure 5,where the “TPR” of the ordinate indicates the accuracy of outlier detection and the “No.of sliding window” of the abscissa indicates the specific window number.

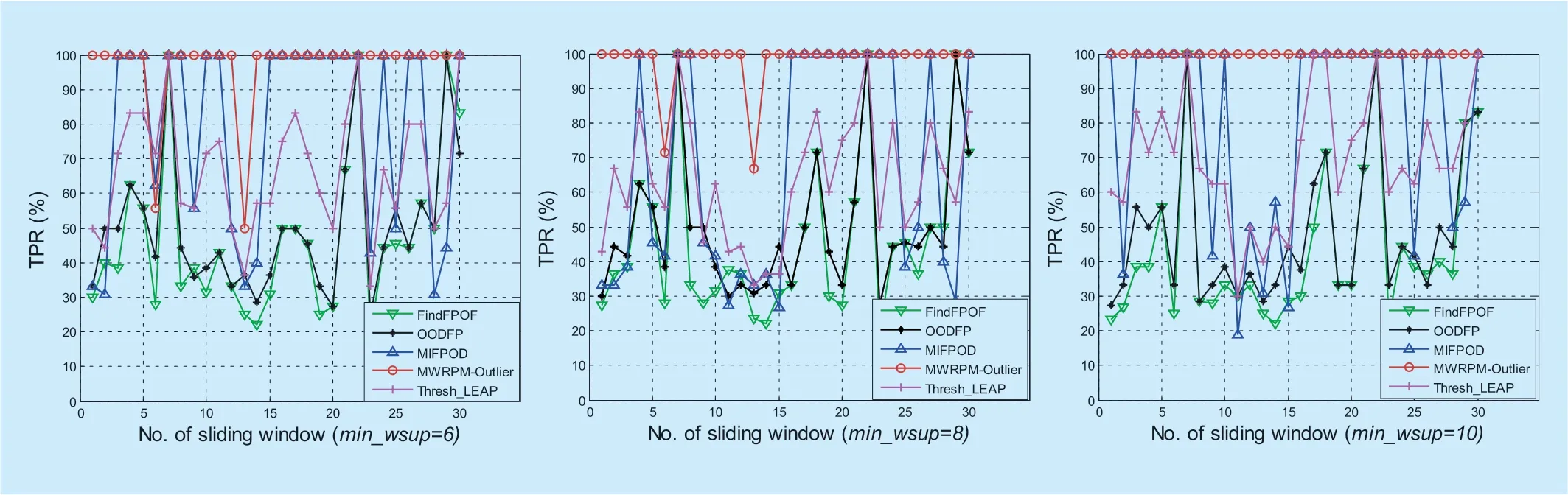
Fig.3.The outlier detection accuracy of MWRPM-Outlier approach when |SW| is 20.

Fig.4.The outlier detection accuracy of MWRPM-Outlier approach when |SW| is 30.

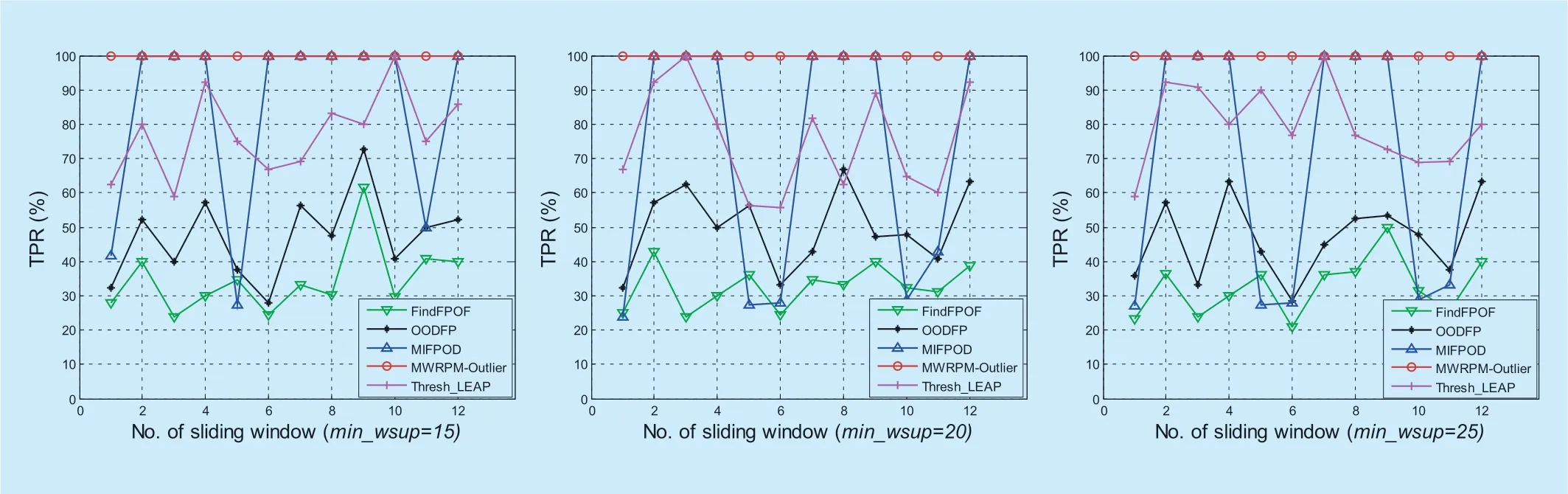
Fig.5.The outlier detection accuracy of MWRPM-Outlier approach when |SW| is 50.

Fig.8.Time cost of the MWRPM-Outlier approach on synthetic dataset when |SW|=50.

Fig.9.Time cost of the MWRPM approach on public dataset mushroom.

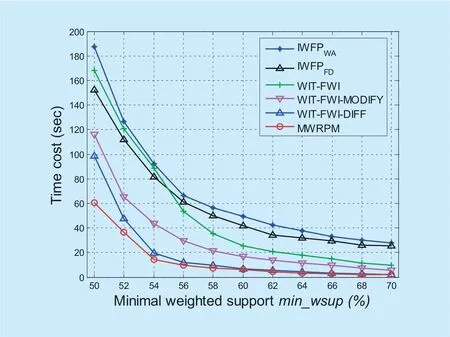
Fig.10.Time cost of the MWRPM approach on public dataset chess.

The outlier detection accuracy of the MWRPM-Outlier approach,FindFPOF approach,OODFP approach,MIFPOD approach and Thresh_LEAP approach is shown in figure 3 to figure 5.As shown in figure 3,when the size of sliding window is 20,the outlier detection accuracy of the MWRPM-Outlier approach is the highest of the five approaches in the case of differentmin_wsupvalues,while the accuracy of FindFPOF approach is the lowest in most cases.When themin_wsupvalues are 6 and 8,there are two windows in the MWRPM-Outlier approach have the misjudgment,where the misjudgment is weaker when themin_wsupvalue is 8.When themin_wsupvalue is 10,the detection accuracy of the MWRPM-Outlier can reach 100%.Among the compared five methods,the detection accuracy of MIFPOD method and Thresh_LEAP method fluctuates greatly.Although the detection accuracy of OODFP approach is slightly better than that of FindFPOF method,but in general,the outlier detection accuracy of OODFP approach is still low.Figure 4 shows the outlier detection accuracy of the compared five approaches when the size of sliding window is 30.When themin_wsupvalues are 9 and 12,the misjudgment is appearing in the fourth sliding window,and when themin_wsupvalue is 9,the misjudgment is more serious than that when themin_wsupvalue is 12.When themin_wsupvalue is 15,the outlier detection accuracy reaches 100%.In general,the detection accuracy of the MIFPOD method and the Thresh_leap method is better than that of the FindFPOF method and the OODFP method,but their detection accuracy fluctuates greatly.In addition,the outlier detection accuracy of the FindFPOF method and the OODFP method can only reach 65%.When the size of sliding window is 50,the outlier detection accuracy of the compared five approaches is shown in figure 5.It is easy to see that the detection accuracy of the MWRPM-Outlier approach is 100% under differentmin_wsupvalues,and the accuracy of other four approaches is also improved.

As can be seen from figure 3 to figure 5,the outlier detection accuracy of the proposed MWRPM-Outlier approach is better than that of other four approaches,and the stability is also the highest.In addition,when the size of sliding window is fixed,the detection accuracy of the proposed MWRPM-Outlier approach will be significantly improved with the increase ofmin_wsupvalues.

5.2 Time cost of MWRPM-Outlier approach

As mentioned in subsection 4.1,the time cost of the whole outlier detection process is composed of minimal weighted rare pattern mining phase and outlier detection phase,while the minimal weighted rare pattern mining phase occupies most of the time.Therefore,in this section,we first use the synthetic dataset to test the time cost of the MWRPM-Outlier approach in the outlier detection phase,where the pattern mining-based outlier detection approaches FindFPOF,OODFP and MIFPOD are used as the compared approaches,and the experimental results are shown in figure 6 to figure 8.Then,we use the public datasetsmushroomandchessto test the time cost of MWRPM approach in the minimal weighted rare pattern mining phase,where the IWFPWA,IWFPFD,WIT-FWI,WIT-FWI-MODIFY and WIT-FWI-DIFF are used as the compared approaches,and the experimental results are shown in figure 9 and figure 10.

Figure 6 shows the time cost of four pattern mining-based outlier detection approaches on a synthetic dataset when the size of sliding window is 20.As can be seen from figure 6,when themin_wsupvalue is 6,the time cost of the MIFPOD approach and MWRPM-Outlier approach is much smaller than the FindFPOF approach and OODFP approach.When themin_wsupvalue is 10,the time cost of the MIFPOD approach and MWRPM-Outlier approach is slightly lower than the FindFPOF approach and OODFP approach.The reason is that when themin_wsupvalue is small,the scale of the patterns that mined from the weighted data stream is very large,but as themin_wsupvalue increases gradually,the number of the mined patterns decreases dramatically.Thus,the time cost of the FindFPOF approach,OODFP approach,MIFPOD approach and MWRPM-Outlier approach is also decreasing rapidly.In addition,the time cost of the compared four approaches generally shows a downward trend with the increase of themin_wsupvalue.

When the size of sliding window is 30,the time cost of the compared four approaches is shown in figure 7.When themin_wsupvalue is 9,the time cost of MIFPOD approach and MWRPM-Outlier approach is relatively close,and the time cost of these two approaches is significantly lower than that of the FindFPOF approach and OODFP approach.When themin_wsupvalue is 12,the time cost of MIFPOD method and MWRPM-Outlier method is essentially the same in most sliding windows,but it is generally close to the FindFPOF method and OODFP method.When themin_wsupvalue is 15,the time cost of the MWRPM-Outlier approach is still smaller than the other compared three methods.In general,as the increase ofmin_wsupvalues,the time cost of the compared four approaches shows a downward trend.

Figure 8 shows the time cost of the compared FindFPOF approach,OODFP approach,MIFPOD approach and MWRPM-Outlier approach when the size of sliding window is 50.As the increase ofmin_wsupvalues,the time cost of the compared four approaches shows a downward trend,in addition,the time cost of the four methods is much closer.

As can be seen from figure 9 that on the datasetmushroom,the time cost of the proposed MWRPM approach is much lower than of the time cost of the IWFPWA,IWFPFDand WIT-FWI,but slightly lower than the WIT-FWI-MODIFY,WIT-FWI-DIFF approaches.With the increase of themin_wsupvalues,the time cost of the six approaches shows a downward trend.This is because the increase ofmin_wsupvalue results in a sharp reduction of the frequent patterns,so that a large number of “pattern extension” operations andsupportvalue calculation operations are omitted.Figure 10 shows the time cost of the MWRPM approach on datasetchess,and the results show that the time cost on the datasetchessis similar to the time cost on the datasetmushroom.Of the six compared methods,the time cost of the MWRPM method is the lowest,and with the increase ofmin_wsup,the time cost of the six compared methods shows a decreasing trend.

VI.CONCLUSIONS AND FUTURE WORK

The traditional distance-based outlier detection approaches,density-based outlier detection approaches and cluster-based outlier detection approaches do not take the appearing frequency of the patterns as a basis for the determination of outlier detection.Therefore,the detected outliers do not fit well with the outliers defined by Hawkins.The pattern mining-based outlier detection approaches have solved this problem,but the existing approaches considered each pattern to be equally important,which deviates from many real situations in real life.Aimed at this problem,this paper presents an efficient minimal weighted rare pattern mining-based outlier detection approach called MWRPM-Outlier to detect the implicit outliers on the weighted data stream,in which the MWRPM-Outlier method is divided into two phases.In the pattern mining phase,we refer to the WITFWI-DIFF approach to propose the minimal weighted rare pattern mining approach,called MWRPM,to effectively mine the potential minimal weighted rare patterns from weighted data stream by using sliding window technology.In the outlier detection phase,we define two deviation factors namelyMWRPDFandTDFto measure the deviation degree of each transaction in the weighted data stream.Finally,each transaction is arranged in decreasing order based on the calculatedTDFvalues,and thektransactions with higherTDFvalue are judged to be outliers.

The detection accuracy and the time cost of the MWRPM-Outlier approach are evaluated on the synthetic dataset,and the experiment is performed in the case of different sizes of sliding window and differentmin_wsupvalues.Experimental results show that the outliers detected by the MWRPM-Outlier approach are closer to the true outliers compared with the FindFPOF,OODFP,MIFPOD and Thresh_LEAP approaches.When themin_wsupvalue is small,the time cost of outlier detection of MWRPM-Outlier approach is much lower than the time cost of the FindFPOF and OODFP approaches.The experimental results on public datasetsmushroomandchessshow that the time cost of MWRPM approach in the minimal weighted rare pattern mining phase is less than the time cost of the IWFPWA,IWFPFD,WIT-FWI and WIT-FWI-MODIFY approaches.Thus,the outlier detection of the MWRPM-Outlier approach proposed in this paper is more efficient.

In the future,we hope to research the minimal weighted rare pattern mining-based outlier detection approach for uncertain weighted data stream.In addition,we also hope to apply the proposed MWRPM-Outlier approach to some real applications,such as agricultural sensor network applications,shopping cart analysis,intrusion detection and so on.

ACKNOWLEDGEMENTS

This work was partly supported by Fundamental Research Funds for the Central Universities (No.2018XD004).