一道对数函数题目的变式探究
■胡 磊 魏 伟
题目 已知函数f(x)=|lnx|,若存在两个互不相等的实数a,b,满足f(a)=f(b),则
分析:设a<b,由函数f(x)=|lnx|去绝对值,即可求解。
解:由函数f(x)=|lnx|=可作出此函数的图像,如图1所示。
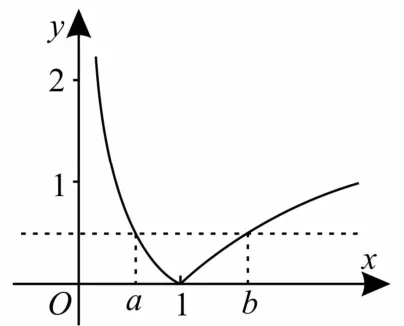
图1
由图像可知,若存在两个互不相等的实数a,b,满足f(a)=f(b),设a<b,则0<a<1,b>1,可得-lna=lnb,即lna+lnb=0,也即lna b=0,故a b=1。
评析:解答本题需要画出函数的图像,根据图像以及对数函数的性质可直观求解。
变式1:已知函数f(x)=|log4x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m5,n]上的最大值为5,求m,n的值。
提示:由f(m)=f(n),根据上面题目可得因为正实数m,n满足m<n,所以0<m<1<n,可得0<m5<m<1<n。结合对数函数的图像可知函数f(x)=|log4x|在区间[m5,n]上的最大值为f(m5)=,解得
注意:解答本题的关键是确定函数在区间[m5,n]上的最大值是f(m5)。
变式2:已知函数f(x)=|log3x|,正实数a,b满足a<b,且f(a)=f(b),若函数f(x)在区间[a2,b]上的最大值为2,则ab=
提示:由于函数f(x)=|log3x|,正实数a,b满足a<b,且f(a)=f(b),所以0<a<1<b,可得-log3a=log3b,即易知0<a2<1<b,所以函数f(x)在区间[a2,1]上单调递减,在区间[1,b]上单调递增,可知当x∈[a2,b]时,函数f(x)在x=a2处取得最大值。由f(a2)=|log3a2|=2|log3a|,可得f(a2)=2|log3a|=-2 log3a=2,解得a=,从而可得故
变式3:已知函数f(x)=|log3(x+1)|,实数m,n满足-1<m<n,且f(m)=f(n),若f(x)在[m2,n]上的最大值为2,则
提示:结合函数f(x)=|log3(x+1)|的图像(图略)求解。由f(x)=|log3(x+1)|,且f(m)=f(n),可得(m+1)(n+1)=1。若f(x)在区间[m2,n]上的最大值为2(f(x)在[m2,n]上单调递增),则log3(n+1)=2,可得n=8,从而可得故应选C。
变式4:已知函数f(x)=|l g(x-2)|,若存在互不相等的实数a,b,使得f(a)=f(b),则的最小值为
提示:若存在互不相等的实数a,b,使得f(a)=f(b),则|l g(a-2)|=|l g(b-2)|,即l g(a-2)+l g(b-2)=0,可得(a-2)(b-2)=1,所以由a>2,可知当时,取得最小值为
——外撇柴

