让学生体验概念建构过程 提高科学思维素养
——以速度概念建构为例
叶晟波
(浙江省慈溪中学 浙江 宁波 315300)
中美贸易的根本问题还是科技教育水平,要提高我国的国际竞争力和教育水平,物理教师必须是为发展学生的核心素养而教.而科学思维作为物理核心素养之一,对其理解和把握的程度会直接影响教学改革的效果.物理概念是人们在认识世界的过程中对客观事物共同属性和本质特征的抽象形成的,它的形成与科学研究方法相对应,在物理教学过程中,掌握物理概念建立过程中的科学研究方法对发展学生的科学思维起到至关重要的作用.本文以速度概念建构过程的研究方法为例,从4个方面去发现概念形成的背后所隐藏着的科学研究方法,发挥这些科学方法的教育价值,把科学方法教育落到实处,从而使物理教学过程成为提高学生科学思维素养的形成过程.
1 速度的定义

初高中对速度的定义都用到了比值定义法,它是物理概念中常用的一种定义新物理量的方法.用两个已知物理量的比值表示一个新的物理量,这个方法利用了控制变量的思维,它的特点是:
(1)被定义的物理量往往是反映物质的最本质的属性.
(2)比值法不随定义所用的物理量的大小取舍而改变,与原来的物理量完全不同.
根据其特点,我们可知物体的速度由物体本身决定,不会随着位移的增大而增大,也不会随着时间的增大而减小.所有的比值法定义的物理量有相同的特点,如电场强度E和密度ρ,通过展开类比与想象,进行逻辑推理、控制变量等思维活动达到初中向高中知识的迁移,提高学生科学思维素养.
2 瞬时速度的建构
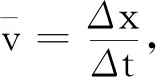
在人教版普通高中课程标准实验教科书《物理·必修1》中对瞬时速度的阐述是: “平均速度只能粗略地描述运动的快慢.为了使描述精确些,可以把Δt取得小一些,物体在从t到t+Δt这样一个较小的时间间隔内,运动快慢的差异也就小一些.Δt越小,运动的描述就越精确.当Δt非常非常小时,我们把这个速度称做物体在时刻t的瞬时速度.”定义中 “当Δt非常非常小时”实际采用了平均速度无限逼近的极限思想方法,它是物理学习中的一种十分重要的科学思想方法,通常是把某一个物理量推向极端,即极大极小或者极左极右,并依此做出科学的推理分析,从而给出判断或导出一般结论的思想方法.数学中的极限思想方法,在物理学习中会逐步渗透.
以上从平均速度的大致描述物体运动的快慢情况到瞬时速度精确地描述物体运动快慢情况,经历了从粗略到精细的研究物理问题的一种方法——修正与逼近.即在分析变速运动的瞬时速度时,采用无限取微元逐渐逼近的方法,即当Δt非常非常小时,在物体经过的某点后面取很小的一段位移,这段位移取得越小,或时间Δt取得越小,物体在该段位移的平均速度越能精确地描述包括该点的运动快慢情况.以上采用无限逼近的极限思想,对培养学生的科学思维素养有非常大的帮助.高中习题中计算平均速度比较方便,只要已知位移和时间即可,那瞬时速度如何计算呢?
3 瞬时速度的计算
复杂的变速运动的瞬时速度比较难计算,高中阶段主要研究了比较简单的匀变速直线运动和匀变速曲线运动瞬时速度的计算公式.
3.1 匀变速直线运动瞬时速度的计算公式
所谓匀变速直线运动就是沿着一条直线运动,且加速度a不变的运动,根据牛顿第二定律,即质点受到的力为恒力,且速度方向与合外力的方向在同一条直线上.清楚匀变速直线运动定义后,可以定量分析其计算公式,物理研究方法中定量分析比定性要难,当然也更精确.初中科学中对许多物理问题往往重在定性分析,即使进行定量计算,一般也是比较简单的,而高中物理,大部分问题不单是定性分析,而且可能要求大量复杂的定量计算.
为了寻求匀变速直线运动的速度特点和规律,可以从具体事例开始.用打点计时器研究小车在重物牵引下的运动如图1所示,此时小车所受的力是恒力,做匀变速直线运动.

图1 用打点计时器研究小车的运动
为了研究实验中速度和时间的关系,先将其在坐标系中描点,然后用一条光滑曲线(包括直线)“拟合”这些点,得到了如图2所示的小车的v-t图像,我们发现匀变速直线运动的v-t图像是一条倾斜的直线,该图像直观地描述了匀变速直线运动的速度v与时间t的关系,将一个较复杂的物理问题简单化、形象化.
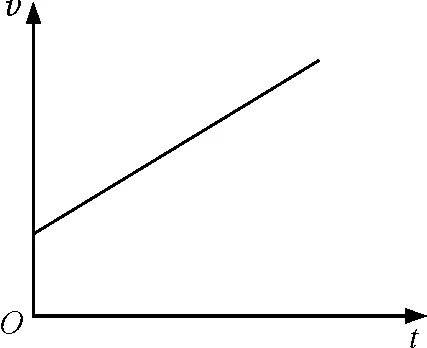
图2 小车的v-t图像
利用图像处理物理问题可以使学生加强对于知识的融会贯通,提高自主学习的能力,对教学也有促进的作用.除了图像方法,根据学生所学的数学知识,可以用公式表达物体运动速度与时间的关系,即速度v和时间t存在一次函数关系,瞬时速度v=v0+at,此公式适用匀变速直线运动.
以上匀变速直线运动瞬时速度计算公式的得出,利用图像法让数形结合,使学生形象思维、灵活处理物理问题的能力得到培养,学生从定性分析运动跨步到了定量研究,这是研究方法和思维上的一个飞跃,大大提高了高中生的物理科学思维.
3.2 匀变速曲线运动瞬时速度的计算公式
匀变速曲线运动也是加速度不变的运动,但是其速度和加速度不在一条直线上,所以运动轨迹是曲线,相对匀变速直线运动更加复杂.怎样把复杂问题简单化呢?我们以比较特殊的匀变速曲线运动——平抛运动为例,可以利用运动的合成与分解的思想来处理.首先建构物体运动的图形,如图3所示,可以把匀变速曲线运动分解成水平方向的匀速直线运动和竖直方向的自由落体运动两个相对简单的直线运动.

图3 分解匀变速曲线运动
如果已知初始时刻的水平速度v0,经过时间t,水平速度v0不变, 水平方向分速度vx=v0,竖直方向分速度vy=gt,则其合速度
设速度方向与x轴成β角,满足
所以合速度v与x轴之间的夹角
应用合成与分解的思想得出了瞬时速度的大小和方向,通过这样的处理让学生认识到无论如何复杂的运动,都可以看成几个简单运动的合成,合运动的效果和几个分运动的效果相同,学生体会到运动的合成与分解是一种分析解决复杂运动的基本方法.这种具体分析问题、解决问题的科学方法,是高中教育给与学生最具有生命力的教育内容,也是学生离开学校后学习和工作的有力工具,因此掌握科学方法,提高学生的思维素养,比掌握具体的知识更具有长远意义.
3.3 瞬时速度的测量
高中是培养创造性思维能力的最佳时机,高中学生动手能力和实验设计能力不断提高,实验中通过瞬时速度的测量可以渗透多种科学方法.
(1)用打点计时器结合纸带可以测瞬时速度,实验器材如图4所示,实验原理如下.
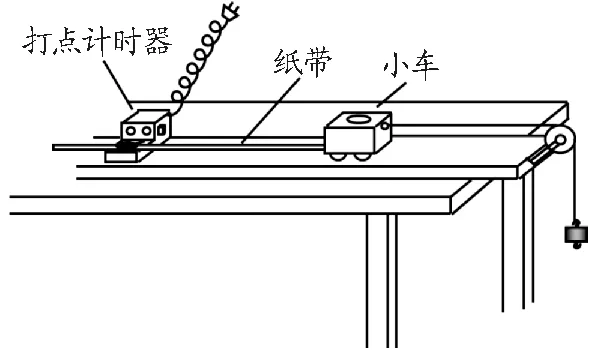
图4 测量瞬时速度实验器材示意图
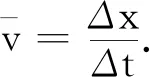
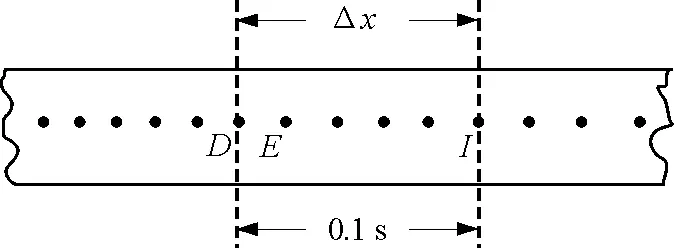
图5 纸带计数点时间间隔取0.1 s

图6 纸带计数点间的时间间隔取0.06 s
我们对实验进一步思考,本实验是用极短时间内的平均速度代替瞬时速度的大小,但是平均速度和瞬时速度是两个不同的概念.这个实验的最小时间间隔只能是0.02 s,并不满足 “非常小非常小”的要求,况且时间太小对应的位移也很小导致位移测量的不精确,所以该实验无法揭示瞬时速度的本质.那么有没有在测量过程中能揭示瞬时速度本质的实验呢?用气垫导轨和数字计时器探究瞬时速度可以做到.
(2)用气垫导轨和数字计时器探究瞬时速度,仪器如图7所示,控制挡光片宽度不变改变光电门位置,实验原理如下.
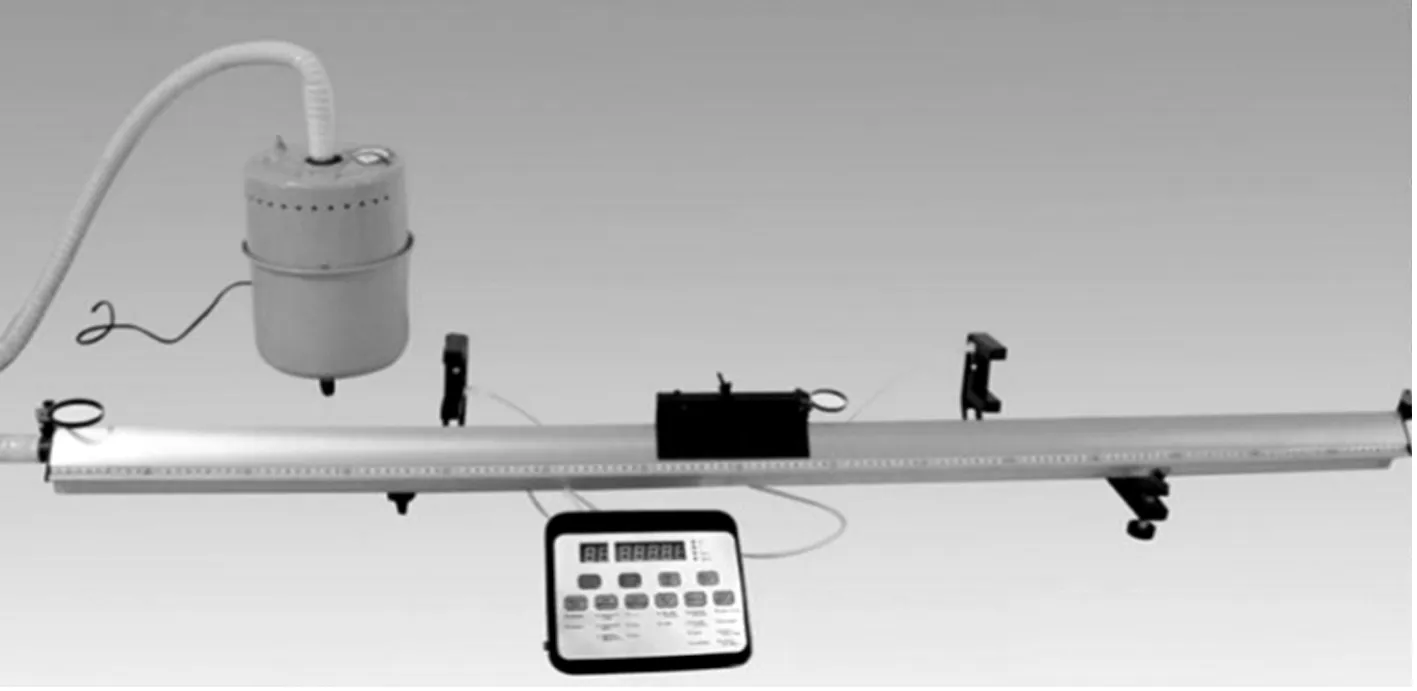
图7 用气垫导轨和数字计时器探究瞬时速度实验
如图8测定滑块通过A点时的瞬时速度,可把一个光电门固定在气垫导轨上的A点,把另一个光电门置于气垫导轨上的B点.研究时,通过改变B点的位置,逐次减少A与B间的距离Δx,分别测出Δx和Δt,计算出对应的平均速度,列出表格1进一步分析平均速度值的变化情况.从表中的实验数据可以看出,随着Δx(亦即Δt)的逐渐减小,各平均速度值也逐渐减小,而且随之接近,Δx=5.00 cm以后,平均值已经趋向于一个定值了,即滑块平均速度已趋向于它通过光电门A时的瞬时速度.不仅如此,我们还可以通过图像法进行理想化外推,如图9所示.从图中可以看出,当光电门之间的距离变到无限小(即时间Δt无限短)时,平均速度的极限值就是挡光片中点通过A点的瞬时速度.Δv-Δx图线在纵坐标轴上的截距29.917 m/s就是Δt→0时的平均速度的极限值——瞬时速度.

图8 测量滑块在A点时的速度

表1 测量数据
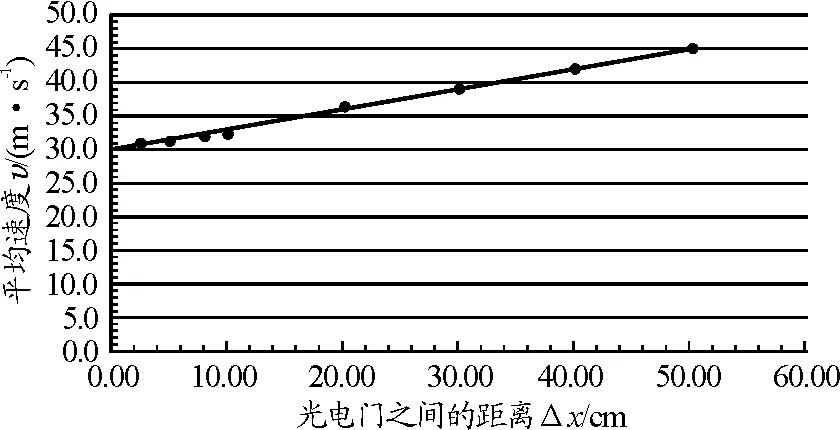
图9 滑块平均速度与光电门间距的关系图像
同理,如果该实验改成用一个光电门,控制光电门位置不变,逐次减小滑块上的挡光片宽度d,分别测出挡光片宽度d和它与之对应的挡光时间Δt,计算出对应的平均速度,再通过Δv-Δd图线的理想化外推,得出的纵坐标轴上的截距就是d→0时的平均速度的极限值——瞬时速度.我们不能让光电门之间的距离Δx或者挡光片的Δd变到无限小(即时间Δt无限短),通过直线的延长交于纵轴的交点,即为无限接近Δt=0,由此推导出来的瞬时速度值的方法,是理想化外推,也是高中阶段重要的科学思维方法.
最有价值的知识是关于思维方法的知识,高中物理在速度概念的建构中应用到了各种科学思维方法,如对比法、比值定义法、极限思想方法、图像法、合成与分解的思想、理想化外推等,它们普遍应用于人的各种思维活动.作为教师要不断探索,根据学生的思维日趋发展,切实让学生体验概念建构过程,努力把前人研究物理现象的思想、方法转化为学生的认识能力和思维方式,从中深刻理解概念的内涵,体会建构概念的外延,让科学方法作为一种素养植根到学生的思想中,使物理教育做到教的是思维,收获的是智慧,真正提高学生的科学思维素养.

