双耦合谐振子共振特性研究
翟立朋 张俊武
(西安交通大学大学物理国家级实验教学示范中心 陕西 西安 710049)
程 琳
(西安工程大学理学院 陕西 西安 710048)
常凯歌 童 童 王雪冬
(西安交通大学大学物理国家级实验教学示范中心 陕西 西安 710049)
共振现象在声、光、无线电、原子物理、核物理及工程领域非常普遍[1],是指在某个特殊频率下系统对外界激发的增强响应,这个特殊的频率通常称为系统的共振频率.早在1602年伽利略研究琴弦振动时就发现了共振现象[2].最简单的共振现象可以用简谐振动模型来描述,其幅频特性曲线是一个对称的洛伦兹线型[2],外驱动力频率接近共振频率时,系统振动的振幅达到最大,达到位移共振,这种共振现象在大学物理理论课上有比较完整的研究[3,4],在大学物理实验教学中常通过波尔共振实验来研究[1].Ugo Fano于1961年在研究原子的自电离态时发现了一类具有反对称线型的新型共振特性[5],这打破了大家对共振现象的认识,这种反对称的新型共振被称为Fano共振.但在大学物理和物理实验教学中,目前针对这种反对称的共振特性涉及较少,所以本文详细研究了双耦合谐振子模型的共振原理及共振特性,并提出了一种可以用于大学物理实验教学的共振仪,以补充大学物理和物理实验教学对共振特性的认识和研究.
1 双耦合谐振子共振原理
如图1所示为双耦合谐振子模型,模型中有A和B两个振子分别连接κ1和κ2两个弹簧,弹簧κ1左端连接周期性的外驱动力Feiωt.

图1 双耦合谐振子模型

(1)
其中x1和x2分别表示A和B两个振子的位移,将式(1)整理之后得到
γBA(κ2)x2=aeiωt
(2)

(3)
式(2)和式(3)中的耦合系数都是只跟弹簧κ2有关的常数,所以两个耦合系数应该是一样的,耦合系数可以简化为
γAB(κ2)=γBA(κ2)=γ
(4)
用待定系数的方法求解由式(2)和式(3)组成的方程组,即可以得到振子A和B的运动特性.
因为A和B两个振子都做受迫振动,所以在振动稳定之后,两个振子都做角频率为ω的周期性运动,方程组解的形式表示为
x1=A1(ω)eiωt
(5)
x2=A2(ω)eiωt
(6)
式(5)、(6)中的指数部分只代表位移是周期性的振动形式,而不包含初相位信息,振子的振幅和相位信息都包含在A1(ω)和A2(ω)中.将式(5)和式(6)所表示的解的形式返回到式(2)和式(3)组成的方程组,进行待定系数求解可以得到
A1(ω)=a·
(7)
A2(ω)=a·
(8)
从式(7)、(8)所表示的A1(ω)、A2(ω)两个物理量可以看出,A1(ω)、A2(ω)都是复数形式,也正好说明了其中包含了振子做受迫振动的振幅和相位信息.所以我们想要研究幅频特性和相频特性,只需要对式(7)、(8)进行分析即可.
A1(ω)和A2(ω)的实部|A1(ω)|和|A2(ω)|代表了振动的振幅信息,即可研究其幅频特性.如果将振幅的相位信息表示为eiφ1(ω)和eiφ2(ω),则A1(ω)和A2(ω)还可以表示为
A1(ω)=|A1(ω)|eiφ1(ω)
(9)
A2(ω)=|A2(ω)|eiφ2(ω)
(10)
将式(9)、(10)相除,并根据欧拉公式,可以得到
ei(φ1-φ2)=eiΔφ=cos Δφ+isin Δφ=
(11)
则有
(12)
(13)
则可以得到两个振子的相位差为
(14)
这样我们根据式(7)、(8)就可以得到振子A和B的幅频特性曲线,根据式(14)就可以得到相频特性曲线.如图2中的(a)和(b)分别表示的是双耦合谐振子模型的幅频特性和相频特性曲线.

图2 双耦合谐振子的幅频特性和相频特性曲线
从幅频特性曲线可以看出,A和B两个振子都对应ω1附近和ω2附近的两个共振峰,说明外驱动力的频率与弹簧振子的共振频率一致时,振动幅度最大,谐振子系统出现共振现象.但是振子A(受到外驱动的振子)在ω2附近的共振峰呈反对称分布,即Fano共振特性.但此处的共振强度相对于普通共振来说要小很多,所以在常规实验中不太容易观察到,也没有得到足够的重视.
将此处的反对称共振曲线放大,如图3所示,可以看出当外驱动力的频率等于ω2时,振子A的振幅出现一个最小值,这是因为弹簧κ1受外驱动力以频率ω2对振子A进行作用时,弹簧κ2带动振子B刚好达到共振状态,使得κ1和κ2对振子A的作用刚好处于反向同步,作用力恰好相互抵消,使振子A刚好达到稳定静止状态,从而出现了振幅最小值,这也是产生非对称共振谱的原因.

图3 Fano共振处的幅频特性曲线
如图2(b)所示,在外驱动力频率为ω2处,振子A和B之间的相位差产生突变,呈反对称线型,即Fano共振的相频特性曲线,与我们之前研究的传统共振中的相频特性[1]有很大的差异.
2 双耦合谐振子共振特性
双耦合谐振子共振特性受两个振子的阻尼系数和耦合系数的影响.本文将具体分析振子A的阻尼β1,振子B的阻尼β2和两个振子之间的耦合系数γ对双耦合谐振子共振特性的影响.
如图4(a)、(b)分别为振子A,B的幅频特性曲线随阻尼β1的改变而产生的变化.从图中可以看出,随着β1的增大,ω1附近的共振峰强度明显减弱,共振峰宽度逐渐增大.对于振子A来说,ω2附近的反对称共振峰的最小值基本没有改变,极大值有微弱的减小趋势,但此处共振峰的线型和半高宽都没有变化;对于振子B来说,ω1处的共振峰强度是有明显减弱,ω2附近的共振峰没有任何变化.这说明β1对ω1附近的共振峰的强度有明显的调控作用,但对ω2附近共振峰基本没有影响.

图4 阻尼β1对幅频特性曲线的调控
如图5(a)、(b)所示分别为振子A,B的共振特性随着振子B的阻尼系数β2的改变而产生的变化.随着β2的增大,两个振子在ω1处的共振峰强度、位置和半高宽都没有变化,而振子A,B在ω2附近的共振峰强度逐渐减小,振子A在此处反对称的振幅最小值从零开始逐渐增大.β2=0时振子B处于无阻尼的理想状态,ω2处的反对称最低值为零,β2越大反对称的最低值和共振峰值越来越接近,Fano共振现象也越来越不明显,直至共振现象逐渐消失.所以想要观察到明显的反对称共振线型,振子B的阻尼系数β2应该尽量的小.

图5 阻尼β2对幅频特性曲线的调控
如图6(a)、(b)所示分别为振子A和B的幅频特性曲线随耦合系数γ的改变而产生的变化.当耦合系数γ为零时,振子A退化为单个谐振子,只有处于ω1附近的一个共振峰,而振子B没有振动,振幅一直为零.随着耦合系数γ的逐渐增大,对于振子A来说,ω1附近的共振峰强度逐渐增强并产生明显红移;ω2附近逐渐产生反对称的共振峰,反对称共振的最低点逐渐降低为零,共振峰的强度逐渐增强并产生明显蓝移,共振峰的半高宽也逐渐增大,反对称线型也越来越不明显.对于振子B来说,随着耦合系数γ的逐渐增大,ω1附近的共振峰强度逐渐增强并产生明显红移,ω2附近的共振峰强度也逐渐增强并产生明显蓝移.

图6 耦合系数γ对幅频特性曲线的调控
对于双耦合谐振子模型的相频特性,从式(14)可以看出,相频特性只受到振子B的阻尼系数β2的影响,与β1和γ无关.如图7所示为振子A,B之间的相位差随阻尼β2的改变而产生的变化情况,两个振子之间的相位差在振子ω2处产生突变.随着阻尼系数的增大,相位突变点没有改变,这也是由式(14)决定的,但相频谱线的半高宽随着耦合系数的增大而逐渐展宽.
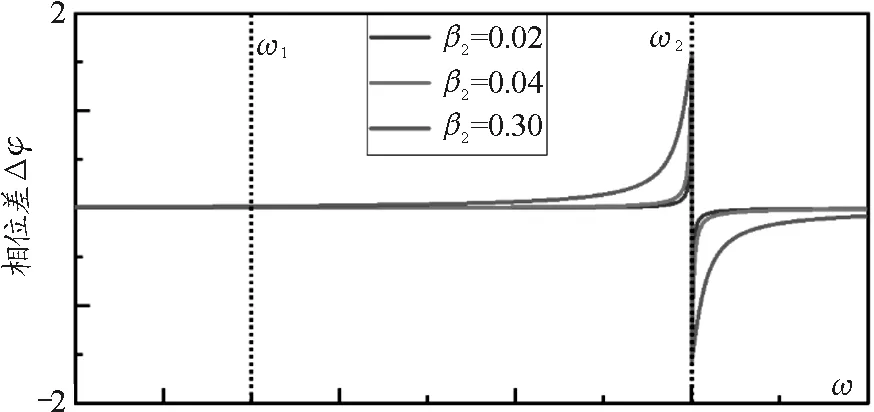
图7 阻尼β2对相频特性曲线的调控
3 双耦合谐振子共振仪
基于本文对双耦合谐振子共振特性的分析,本文提出一种双耦合谐振子共振仪,可用于大学物理实验教学,以填补学生对反对称线型共振现象的认识.
如图8所示为共振实验仪的模型图,本文提出的共振实验仪由驱动系统、测量系统和控制系统3个系统构成.

图8 双耦合谐振子共振仪示意图
控制系统设置外驱动力的参数和测量后的数据记录.在驱动盘的圆周边缘均匀刻上一周狭缝(示意图中只画出了4条狭缝),称为驱动相位测量尺.驱动电机带动驱动盘转动,在狭缝通过左侧光电门的过程中,光电门可根据狭缝的长度和通过狭缝的数目确定外驱动的相位,这与目前大学物理实验中用到的波尔共振仪类似[6].外驱动通过驱动杆传动到测量系统的驱动振子,使驱动振子产生周期性振动,驱动振子通过弹簧κ1和κ2分别驱动振子A和B振动,为了测量振子A和B振动的振幅和相位,在每个振子上加一个光电门,光电门经过下方刻有狭缝的位移相位测量尺,光电门根据通过测量尺的狭缝数目确定受迫振动的振幅、相位和振动频率等参数,最后将测量结果回传到控制系统,得到我们想要的振子A,B的振幅和相位信息,从而描述双耦合谐振子模型做受迫耦合振动的幅频特性和相频特性.
4 结论
本文详细推导了双耦合谐振子做受迫振动的幅频特性和相频特性,在外驱动频率等于振子B的共振频率ω2时,振子A会产生反对称的Fano共振.阻尼系数β1和β2分别调控ω1和ω2附近的共振强度,耦合系数γ对两个位置的共振峰都有影响;相频特性曲线只受阻尼系数β2的调控,阻尼系数β2和耦合系数γ可以调控Fano共振的幅频特性和相频特性.想要观察到明显的Fano共振现象,阻尼β2应该尽量的小.本文所提出的双耦合谐振子共振仪可以同时测量反对称的Fano共振特性和常规对称的共振特性.

