基于双序列的联合跳频通信模式

赵祥武，全厚德，崔佩璋

(陆军工程大学石家庄校区，河北 石家庄 050003)

0 引言

传统跳频中跳频信号伪随机的跳变，用户数据与所在信道没有相关性，如果有用信号被敌方干扰到，那么接收端都无法准确获得信息。通过时频分析，有机会可以判决有用跳频信号所在的哪个信道[1]。这表明信道固有的某些特性(即信道描述符[2])可以很好地检测出来，如果直接用信道的固有特性来区别不同的信号，就不需要调制信号，并且还可能取得更理想的实用效果，抗干扰性能更优。正是由于这样，差分跳频(Differential Frequency Hopping,DFH)[3],消息驱动调频[4]以及M元多级FSK跳频通信中都利用了信道的固有特性这一思想，跳频信号当前所在的信道是用户信息的函数，由于接收机没有提前获得信道的某些信息，一般情况下使用宽带接收技术。值得注意的是美国研发的差分跳频电台在抗干扰方面性能尤为突出[5-7]，但是差分跳频在硬件方面较为复杂，组网困难，某种情况下比传统跳频通信性能略差。由于传统跳频通信抗跟踪干扰的较差，本文针对上述问题，提出了基于双序列的联合跳频通信模式(Binary-Sequence Frequency Hopping，BSFH)。

1 基于双序列的跳频系统模型

在BSFH中，跳频通信系统内带宽W内包含M个跳频的频点。发送机与接收机间存在L=2个信道，每个跳频点在某一时刻存在于一个信道内，这个跳频点被该信道所拥有的跳频序列决定，这个联合跳频通信系统总共有L个跳频序列构成，每一跳所传输的符号数B=lbL。

收发双方的两条信道分别定义为子信道0和子信道1，对应着有两条跳频序列HS0和HS1。设比特能量是Eb，持续时间记为Tb。所以发射机符号能量Es=BEb，符号持续时间Ts=BTb。假如用户数据选择的是0，此时跳频信号存在于信道0中，所以跳频序列HS0中信号s0(t)进行跳变；假如用户数据选择的是1，此时跳频信号存在于信道1中，所以跳频序列HS1中信号s1(t)进行跳变，如图1所示，正是由于HS0和HS1正交，联合跳频系统保持跳频同步，所以发射机发送到空中的信号s(t)表示为s0(t)与s1(t)的组合。跳频信号进行跳变时每一跳发送一个符号数据。所以发射机发射的基带信号可以写作：

(1)

发射机将跳频信号通过射频前端传输到空中，由于空中电磁环境存在噪声以及信道衰落，还有各种干扰。接收端接收到的跳频信号基带表示为：

r(t)=αsejθs(t)+n(t)+J(t)

(2)

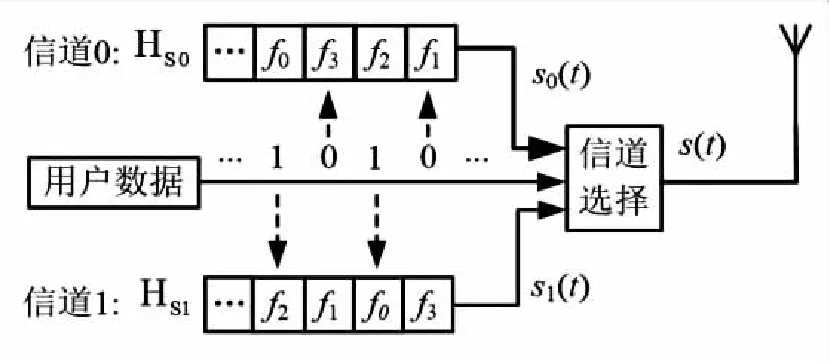
图1 BSFH发射机示意图Fig.1 BSFH transmitter schematic diagram

接收机在两个独立的信道上并行接收跳频信号，都采用窄带接收的方式，如图2所示。

图2 BSFH接收机示意图Fig.2 BSFH receiver schematic diagram

接收机本地的伪随机码产生器产生的两路跳频信号分别与HS0和HS1同步。某一时刻，接收到的跳频信号r(t)分别与信道0和信道1在当前时刻的频点进行频率混频，再经过窄带滤波之后以及平方率非相干检测后。非相干的检测的结果Ri(i=0,1)表示为：

(3)

判决量Y可以定义为Y=R0-R1，然后通过判决结果分析发射信号所在的信道，进而恢复出跳频信号。我们可以采取最为简便的判决方案，即硬判决，当Y≥0时，我们认定此时发射信号为s0(t)；当Y≤0时，我们认定此时发射信号为s1(t)。

相较于传统跳频通信，双序列联合跳频通信不需要对载波进行调制，依赖的是载波的差异性代表跳频信号。这样对发射的跳频信号进行干扰导致该跳频信号的能量增大，更利于检测。而且与传统跳频不同的是，传统跳频通信在数据信道和对偶信道中有固定的频率间隔，而BSFH的两个信道间隔是伪随机的发生着变化，即便干扰到了一个信道，也很难获得另一个信道的频率跳变规律，可以有效地规避敌方的干扰[8-10]。

2 BSFH抗干扰性能分析

AWGN信道模型作为基本的信道模型，对于AWGN信道来说，其中α=1。在无干扰的状态下，J(t)=0。接收信号表达式。可写为

r(t)=ejθs(t)+n(t)

(4)

若AWGN信道中没有出现任何干扰，根据双序列联合跳频系统模型可得，双序列联合跳频通信的误码率与传统跳频通信的误码率是一样的，记为：

(5)

在双序列联合跳频模型中，有B=1，L=2，Es=BEb=Eb。信噪比表示为：

(6)

信干比表示为：

(7)

2.1 抗跟踪干扰性能分析

在双序列联合跳频通信系统中，接收端接收跳频信号的判决结果Y=R0-R1取决于接收信号与两个子信道的非相干检测的结果。假定跟踪干扰是窄带噪声干扰，两个子信道的非相干检测的结果是独立的，跟踪干扰干扰有用的跳频信号的干扰成功率为β，而且干扰时间比例设定为ρT，干扰带宽比例设置为ρW，在跳频信号传输中，假定gi表示子信道的非相干检测的结果Ri被跟踪干扰到或者未被跟踪干扰到，其中gi=1表示被干扰，gi=0表示未被干扰。pRi(ri|gi)定义为第i(i=0,1)个信道的干扰结果为gi时Ri的密度函数(Probability Density Function，PDF)。为了找到跟踪干扰对双序列联合跳频通信系统的影响，本节先不考虑其他干扰，所以n(t)=0。r(t)重新定义为：

r(t)=ejθs(t)+J(t)

(8)

信道0的非相关检测结果的密度函数在没有跟踪干扰时为δ分布，但要是受到了跟踪干扰时为莱斯分布，即：

(9)

(10)

δ(x)代表狄拉克函数，I0(x)代表第一类0阶修正贝塞尔函数；U(x)为单位阶跃函数。

而子信道1的非相关检测结果的密度函数在没有跟踪干扰时为δ分布，但要是受到跟踪干扰时为瑞利分布，即：

pR1(r1|0)=δ(r1)

(11)

(12)

设定Gj=(g0g1)为判决结果Y的干扰情况，其中j=0,1,2,3。Gj跟g0，g1的状态表示如表1。

表1 判决结果的干扰状态Gj和子信道的干扰情况gi的关系

那么Gj的概率表示为：

P(G0)=P(g0=0)P(g1=0)=(1-β)(1-ρW)

(13)

P(G1)=P(g0=0)P(g1=1)=(1-β)ρW

(14)

P(G2)=P(g0=1)P(g1=0)=β(1-ρW)

(15)

P(G3)=P(g0=1)P(g1=1)=βρW

(16)

Pj表示干扰判决状态为Gj时双序列联合跳频通信系统判决的错误概率。本文选择使用择大判决：

(17)

(18)

(19)

(20)

定义比特误码率为Pb，跳频信号判决错误概率为Pe，可得

(21)

(22)

将式(13)—式(16)，式(17)—式(20)代入公式(22)中，并根据γJ=Eb/NJ，可得：

(23)

2.2 抗部分频带干扰性能分析

在部分频带干扰中ρT=1，β=ρW=WJ/W，所以跳频信号在部分频带干扰的干扰下，接收机的判决结果的干扰情况Gj(j=0,1,2,3)的概率表达式为：

P(G0)=(1-ρW)2

(24)

P(G1)=ρW(1-ρW)

(25)

P(G2)=ρW(1-ρW)

(26)

(27)

将式(17)—式(20)，式(24)—式(27)代入式(2)—式(22)，在双序列联合跳频的比特误码率为：

(28)

为了便于分析，令

Pb1=(1-ρW)ρWexp(-γJρW)

(29)

(30)

即

Pb=Pb1+Pb3

(31)

3 仿真结果分析

假设BSFH由两个跳频序列组成，并且序列间相互正交，跳频通信有两个信道传输信息。在收发两端已经完成同步的情况下，由于跟踪干扰只能截获数据信道的跳频频率，而不能干扰到对偶信道的频率。所以跟踪干扰可以随着跳频信号数据信道的频率跳变规律跳变，仿真分析跳频通信中跟踪干扰与部分频带干扰性能时，假定信道不考虑噪声的存在。

3.1 BSFH误码率仿真结果分析

AWGN信道条件下，双序列联合跳频在跟踪干扰和部分频带干扰下仿真结果与数值的结果如图3所示。跟踪干扰的参数取合理的数值时，通过仿真的最后结果与数值计算大致在一条曲线上，说明系统模型理论推导正确；从图中可以看出实际中的跟踪干扰效果跟部分频带相比并没有明显很多。初步可以看出双序列联合跳频有一定的的抗跟踪干扰性能。

图3 BSFH误码率数值与仿真结果比较Fig.3 Comparison of BSFH BER numerical and simulation results

3.2 干扰成功率β的仿真分析

就跟踪干扰的干扰成功率β这一参数，分别对比了双序列联合跳频与常规传统跳频的误码率，假定BSFH与FH的带宽相同，比特传输速率相同，如图4为跟踪干扰成功率的仿真结果，β取得典型值0.3,0.7，1，而其他两个参数干扰时间比例，带宽比例在都相同，假定ρT=1，ρW=1/8。

图4 BSFH和FH误码率在干扰成功率β条件下的仿真分析Fig.4 Simulation analysis of BSFH and FH bit error rates under jamming success rates β

从图4中可以看出：当干扰成功率取值相同时，在相同信干比的条件下，双序列联合跳频误码率明显小于传统跳频通信的误码率，当误码率达到10-6时，相同干扰成功率的两种跳频通信模式的信干比相差3～4 dB,这是由于跟踪干扰仅干扰到数据信道的频率，而没有截获对偶信道的频率信息，所以抗跟踪性能有明显的提升；当信干比大于17 dB时，干扰成功率越大，跳频通信系统的误码率也就越大，反之，当信干比小于17 dB时，扰成功率越大，跳频通信系统的误码率就越小，原因就是当强干扰信号干扰数据信道时，这样反而会增加跳频信号的能量，更利于检测模块进行判决。取极限的情况分析时，干扰成功率取值1，干扰时间比例也取值为1，干扰带宽为1/32,在不考虑噪声干扰的情况下，计算可得双序列联合跳频系统误码率为零。

3.3 干扰时间比例ρT的仿真分析

图5是干扰时间比例的仿真结果，ρT取典型值0.2,0.6,1，而其他两个参数干扰成功率，带宽比例在BSFH和FH中都取值一样，假定β=1，ρW=1/8。由图5中可以看出干扰时间比例越小，干扰误码率就越小，意味着不易成功进行干扰，在相同信干比的前提下，双序列联合跳频通信的误码率明显小于传统跳频的误码率，同样的是，对于BSFH与FH而言，时间比例的增加，干扰误码率就会增大，在相同误码率10-6的前提下，对于同一干扰时间比，双序列联合跳频通信比传统跳频通信的信干比低1.5 dB。

图5 BSFH和FH误码率在干扰时间比例ρT条件下的仿真分析Fig.5 Simulation and analysis of BSFH and FH bit error rates under the condition of time-to-interference ratio ρT

3.4 干扰带宽比例ρW的仿真分析

图6是干扰带宽比例的仿真结果，ρW取典型值1/8,1/4,1，而其他两个参数干扰成功率，干扰时间比例在BSFH和FH中都取值相同即β=1，ρT=1，在ρW=1时双序列联合跳频与传统跳频的误码率仿真结果相同，在相同的信干比的前提下，传统跳频的误码率随着干扰带宽比例的增加而减小，而双序列联合跳频表现的有所区别，在信干比小于10 dB下，误码率随着干扰带宽比例的增加而增大，当信干比超过10 dB时，干扰带宽比例越大，误码率越小，因为小信干比的情况下，跟踪干扰的功率足够的强，在宽带干扰上更容易获得更好的效果，所以在小信干比下，最后的干扰变成了宽带干扰。

图6 BSFH和FH误码率在干扰带宽比例ρW条件下的仿真分析Fig.6 Simulation and analysis of BSFH and FH bit error rates under the ratio of interference bandwidth ρW

从整体仿真结果分析，在确定的干扰带宽中，双序列联合跳频的误码率比传统跳频的误码率低，当干扰带宽比为1/8时，误码率为10-6时，双序列联合跳频通信比传统跳频通信的信干比低2 dB。

在AWGN信道下，通过以上对于干扰成功率、干扰时间比例、干扰带宽比例的仿真结果可以看出，双序列联合跳频通信的抗跟踪干扰性能明显优于传统跳频通信。

4 结论

本文提出了双序列联合跳频的通信模式，该模式以跳频序列作为信道描述符，而不需要进行信号的调制，同时让数据信道和对偶信道各自独立的依靠不同的序列进行跳频，这样大大减少了跟踪干扰能够干扰到对偶信道的可能性，削弱了跟踪干扰的性能。仿真验证结果表明，双序列联合跳频有着较好的抗跟踪干扰性能，在误码率为10-6时，双序列联合跳频通信比传统跳频通信的信干比低约2 dB。