基于长短时记忆网络的仿真系统数据故障诊断方法
牛 群,刘志永,褚建川,王艳奎,吴根水
(中国空空导弹研究院,河南 洛阳 471099)
0 引言
系统仿真是广泛用于系统工程各个研制阶段的一种极其重要的技术,用于复现和评价真实系统。空空导弹仿真系统是空空导弹研制过程中不可缺少的评价鉴定手段,其在试验室条件下,以较低的代价和较高的置信度,获得空空导弹在各种条件下完整的性能数据,通过试验数据分析可实现系统性能设计、批量生产质量、作战运用、性能价格比等方面的优化。空空导弹仿真系统的数据分析工作仍旧以人工分析为主,其工作依赖人工专家的个人知识和过往经验。随着空空导弹型号研制的增多与试验数据的累加,一方面,人工分析依赖数据分析专家,面对海量的试验数据分析效率低下,有心无力;另一方面,人工分析在海量数据的数据挖掘和隐藏规律发现方面,存在有效信息漏读、漏判和误判的现象。
吴国文提出了基于深度信念网络(Deep Belief Network,DBN)的故障诊断方法,将分类准确率提高至93.3%;文献[1]提出了基于BiLSTM的齿轮故障诊断方法,齿轮故障诊断准确率高于80%。但是,时间序列中的故障信息与时间尺度有直接联系,单一尺度诊断模型并不能有效识别仿真数据的关联故障信息[2-4]。本文从多层次数据分析需求出发,提出基于长短时记忆网络(long short-term memory,LSTM)的仿真数据故障诊断方法。通过分析仿真试验数据的数据特征,为满足系统仿真实验过程所产生数据进行多尺度分析的任务需求,针对时序故障数据可能存在“长、中、短”时的多尺度特性,拟利用试验过程数据建立基于长短时记忆的多尺度深度神经网络模型,通过在深度神经网络中设计多尺度层次结构,使输入端数据从不同深度进入网络。在此基础上,采用长短时记忆网络将健康数据中的时序信息进行记忆,并内嵌至所建立的深度神经网络模型,从而有效表征健康数据的本征变化属性,进而对试验过程中的故障数据进行准确诊断。
1 LSTM网络简介
1.1 LSTM结构
长短时记忆网络(LSTM)是一种特殊的RNN类型,可以对数据的长期依赖关系进行学习,可将输入的仿真时序数据中有效信息记录在节点状态中,同时将节点状态中无效信息遗忘,可以对时序故障数据特征进行有效表征[3-4]。
LSTM基本结构单元又称作记忆块,它代替传统神经元单元组成LSTM网络。记忆块由1个中心节点和3个门控单元组成。3个门控单元与中心节点分别相连,分别称作输入门、输出门和遗忘门,它们控制信息流入,中心节点称作记忆细胞,用于存储当前网络状态[5-6]。在前向传递中,输入门控制输入到记忆细胞的信息流,输出门控制记忆细胞到网络其他结构单元的信息流;在后向传递中,输入门控制误差流出记忆细胞,输出门控制误差流入记忆细胞。遗忘门控制记忆细胞内部的循环状态,决定记忆细胞中信息的取舍(遗忘)。LSTM的这种门控机制是让信息选择性通过,使记忆细胞具有保存长距离相依信息的能力,并在训练过程中防止内部梯度受外部干扰。每个记忆细胞都存在一个自循环连接线性单元,称为恒定误差传送带,使误差在内部以恒定值传播,避免了梯度消失和梯度爆炸问题[7-8]。
LSTM网络由多个节点连接而成,节点的结构如图1所示。
节点的输入包含当前时刻的输入数据X(t)和前一节点的输出数据Y(t-1)。
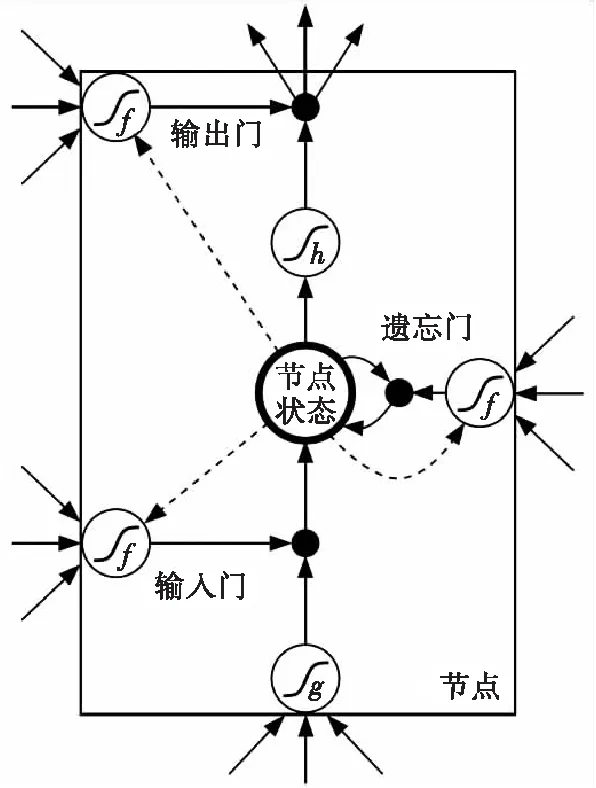
图1 LSTM网络节点图Fig.1 LSTM network node graph
输入门负责将这些输入信息根据节点状态,通过一组学习得到的权重对输入数据进行整合:
(1)
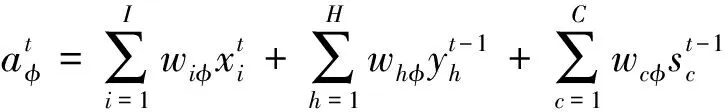
随后可以根据输入信息和遗忘信息对节点状态进行更新,将现有状态与遗忘系数相乘,再补充上输入的新信息,得到当前时刻的节点状态S(t):
(2)
式(2)中,g(·)为激活函数。最后,根据当前状态与输入信息经过输出门得出节点输出:
(3)
式(3)中,h(·)为激活函数。
1.2 LSTM网络模型训练
LSTM网络模型采用误差反向传播算法对网络进行训练学习[9]。反向传播的主要思想就是先训练样本输入网络得到一个输出结果,利用输出结果与标注的标准结果的残差计算损失函数梯度,根据梯度的反向传播,将残差反馈到网络中的每个权重上,可以计算出每个权重的调节量δ[10]。
首先通过前向传播计算在时刻t时网络的输出向量,则总的误差值定义为L,定义:
由于节点输出梯度与输出层权重调节量的关系为:
可以得出输出门权重调节量为:
同时基于节点状态梯度:
可以进一步得出节点状态权重调节量、遗忘门权重调节量和输入门权重调节量:
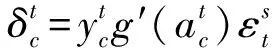
利用多组数据对网络参数进行反复调整,逐渐逼近最佳的权重参数,最终可以得到一组使损失函数最小的参数,使网络模型最优。
2 基于LSTM的仿真数据故障诊断模型
本文采用LSTM神经网络对空空导弹仿真系统数据进行诊断分析,首先采用三点拉格朗日插值法保证LSTM神经网络数据分析的可行性与有效性,然后设计LSTM故障诊断网络模型,最后设计仿真系统数据故障诊断模型,将其运用于空空导弹仿真系统数据分析。
2.1 参数时间校正方法

(4)
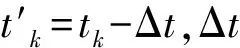
2.2 基于LSTM的故障诊断网络模型
LSTM模型的建模能力取决于记忆块中记忆单元的数目,而随着输入LSTM的序列长度的增加,LSTM的性能会逐渐变差。
由于空空导弹仿真系统数据具有数据量大、数据时间序列复杂的特点,为保证LSTM的性能,本文提出了一种层次化的LSTM模型结构,完成空空导弹仿真系统数据深度神经网络的建模,该网络模型由两层独立的深度学习神经网络模型构成。仿真系统数据首先进入LSTM神经网络层,实现仿真系统数据“长、中、短”三种长度时间序列的网络神经网络模型建模与故障诊断,诊断结果进入RBF神经网络层,实现故障诊断结果分类,最后输出故障诊断结果,实现仿真系统数据多尺度故障诊断[11-12]。
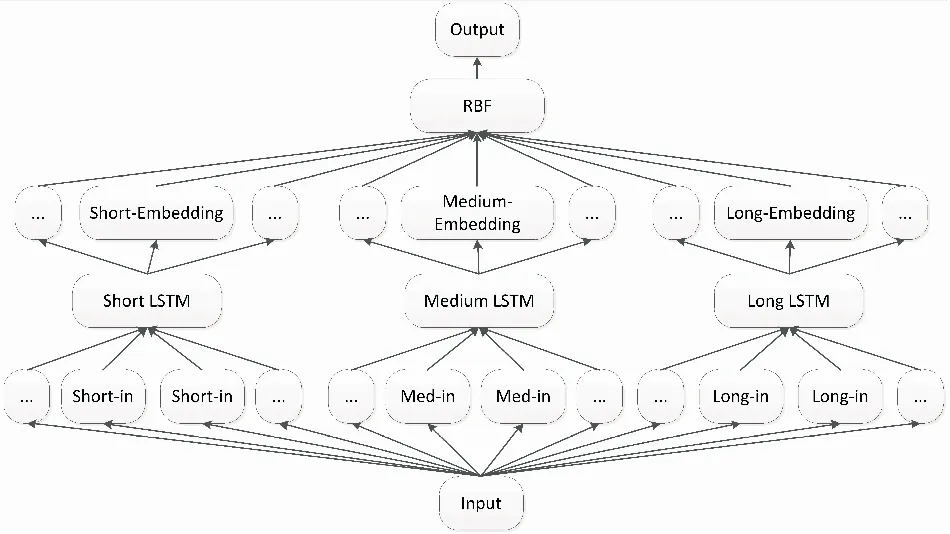
图2 LSTM数据故障诊断网络模型Fig.2 LSTM data fault diagnosis network model
2.3 仿真系统数据故障诊断软件
故障诊断网络模型建立后,利用专家标注库和快速数据预处理方法,从而设计高效的空空导弹仿真系统数据故障诊断软件,仿真系统数据故障诊断流程图如图3所示。
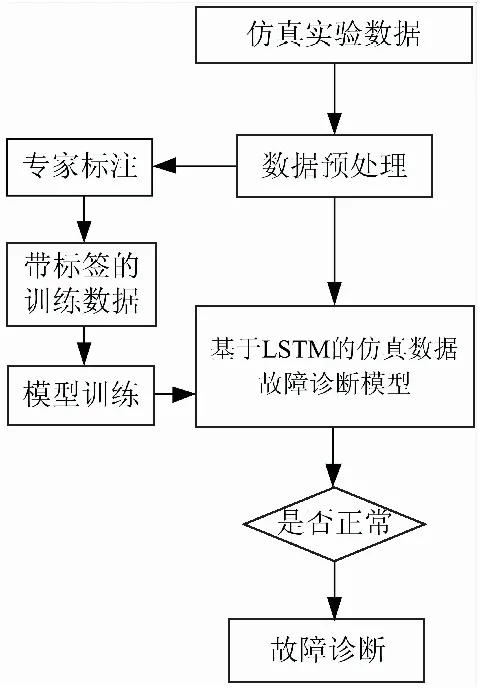
图3 LSTM网络故障诊断流程图Fig.3 Flow chart of LSTM network fault diagnosis
3 实验验证与结果
为了衡量本文方法的性能,采用空空导弹仿真系统数据进行实验,以故障诊断准确率作为性能评价指标进行测试。
本文首先使用大量健康空空导弹仿真系统数据对基于LSTM的仿真数据故障诊断模型进行训练,令仿真数据故障诊断模型达到最优,选取一组特点明显角速度数据,输入模型进行故障诊断,以验证本文方法的有效性。
相同仿真条件下,数字仿真角速度数据为omz1,半实物仿真角速度数据为OMZ_Ap,两组角速度曲线如图4所示。

图4 角速度曲线Fig.4 Angular velocity curve
首先将omz1所在的数字仿真数据组输入LSTM故障诊断模型,LSTM故障诊断模型显示此组数据正常,并给出仿真系统故障概率与仿真系统分系统故障概率。
omz1数组仿真系统故障概率如表1与图5所示。omz1数组仿真系统分系统故障概率如表2与图6所示。

表1 omz1数组仿真系统故障概率
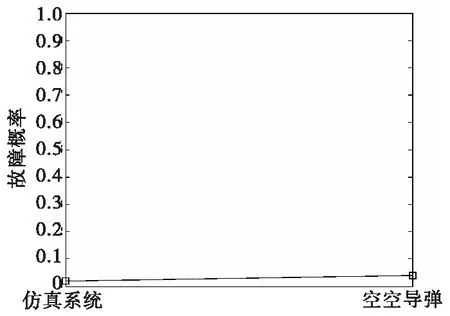
图5 omz1数组仿真系统故障概率Fig.5 Simulation system failure probability of omz1 array

故障点总控系统仿真机信号源系统转台系统故障概率0.050.040.040.02

图6 omz1数组仿真系统分系统故障概率Fig.6 Simulation system subsystem failure probability of omz1 array
如上表、图所示,仿真系统故障概率和空空导弹故障概率很小,仿真系统各分系统故障概率也均小于5%,此组数据未出现故障。另外,由于omz1数组为数字仿真数据,仿真系统数据为理想数据,仿真系统故障概率小于空空导弹故障概率,本文故障诊断结论符合该组仿真系统数据真实情况和故障诊断专家经验,则此方法针对数字仿真系统数据有效。
然后将OMZ_Ap所在的半实物仿真数据组输入LSTM故障诊断模型,LSTM故障诊断模型显示此组数据存在故障,并给出仿真系统故障概率与仿真系统分系统故障概率。
OMZ_Ap数组仿真系统故障概率如表3与图7所示。OMZ_Ap数组仿真系统分系统故障概率如表4与图8所示。

表3 OMZ_Ap数组仿真系统故障概率

图7 OMZ_Ap仿真系统故障概率Fig.7 Simulation system failure probability of OMZ_Ap

故障点总控系统仿真机信号源系统转台系统故障概率0.080.030.010.92

图8 OMZ_Ap数组仿真系统分系统故障概率Fig.8 Simulation system subsystem failure probability
表3中仿真系统故障概率为93%,空空导弹故障概率为7%,仿真系统故障概率远远大于空空导弹系统故障概率,表4详细描述仿真系统各分系统故障概率,其中转台系统故障概率为92%,远大于其他系统的故障概率,则本文方法判定仿真实验过程中转台系统出现异常,导致此组仿真数据与健康存在一定差异。通过仿真专家分析,此组半仿数据实验时存在转台未对准情况。故本文故障诊断结论符合该组仿真系统数据真实情况和故障诊断专家经验,则此方法针对半实物仿真系统数据有效。
4 结论
本文提出基于长短时记忆网络的仿真系统数据故障诊断方法,该方法是基于LSTM网络的层次化优化。实验表明,本方法在保证LSTM网络性能的前提下,实现对仿真系统数据故障的诊断,同时,随着数据不断输入与模型不断训练学习,此诊断模型的准确率将不断提高。然而,故障诊断过程中故障标签仍由专家经验组成,之后工作中将着重研究故障概率阈值选取问题。

