一种面向无向加权图的子图查询方法

朱 磊,姚燕妮，高 勇，王一川，姬文江，黑新宏，刘 征

(1.西安理工大学 计算机科学与工程学院，陕西 西安 710048；2.西安理工大学 自动化与信息工程学院，陕西 西安 710048)

图被大规模用于构造半结构或非结构化的数据和语义。例如，化学[1]、社交网络[2]、知识图谱[3]、XML文件[4]等。在这些应用中，实体和关系被建模为图模型，并构建更加高效的半结构或非结构化的图数据库，然后应用图挖据相关技术去高效智能地检索事物间的关联关系[5]。

图数据库相关领域中，子图查询过程包含子图同构的判定，而该问题已经证明是NP完全问题[6]，所以现存的方法均采用过滤-验证框架，而且提取高效的图特征进行过滤已成为子图查询的重要研究方向。一些现存的方法主要采用数据挖掘的理论去提取频繁子结构作为特征，并使用倒排序的索引进行过滤[7,8]。但是这类方法在图数据频繁更新时，必须重新挖掘频繁子结构和建立索引，导致代价过大[9]。

针对无向加权图，本文提出了一种子图查询方法PSQuery，提取的主要特征包括：节点标记、边、最短权值路径和拉普拉斯图谱信息。将这些信息特征分别按照不同方法进行编码，形成节点和图编码，基于图编码构建索引树进行过滤。在遍历索引树后生成候选图集合，再采用经典VF2算法进行子图同构验证，得到最终的结果集。通过在真实数据集和合成数据集上的实验结果对比，验证了本文所提方法提高了子图查询的效率。同时，由于PSQuery方法不以频繁子结构作为图的特征，因此提出的方法可以很好地处理图库频繁更新的情况。

1 相关工作

定义：(无向加权图)给定无向加权图G=〈VS,ES〉，其中VS和ES分别为节点集合和边集合。图中每个节点v可以建模为二元组〈vid，vlable〉，表示节点的ID和标记。每条边e建模为三元组〈vi，ew，vj〉，用于表示节点vi和vj间的无向边，其边权值为ew。

定义：(子图查询)给定一个图数据库D和一个查询图Q，其中数据集包含n个数据图,D={G1,G2, …,Gn}。子图查询的目标是在D中找到Q的所有超图集合。

在具体查询过程中，涉及的难点是查询中包含了子图同构的判定，而该问题已经被证明是NP完全问题。所以，现存的方法通常采用过滤-验证框架去加速子图查询过程，目的是减少子图同构判定的次数。

在子图查询的相关工作中，Closure-Tree方法将相同子结构聚簇为闭包，并且对闭包建立索引树[10]。在遍历索引树时进行过滤，将不符合条件的闭包删除，生成候选图；在过滤时，采用子图同构的判定方法进行验证，得到结果集。但是，该方法在过滤时采用类似子图同构的判定方法进行检测，导致该方法在过滤阶段花费较高的代价[9]。

为了减少过滤阶段的判定开销，一些方法使用数据挖掘的算法，提取频繁子结构建立倒序索引。在遍历索引时，对查询图不包含的频繁子结构进行过滤，通过子图同构算法进行验证得到结果集。例如，Graphgrep[11]采用路径建立索引。而gIndex[7]、Swiftindex[8]、FG-gindex[12]、Treepi[13]等方法挖掘频繁子图或者子树作为索引特征。这类方法在构建索引的过程中花费的代价较大，所以在图数据频繁更新时，这类算法由于必须重新挖掘频繁子结构和建立索引，导致代价过大[9]。

为了避免上述问题，第三类方法是将图的结构信息映射到数字空间，使用表示学习的方法生成编码，并且在编码的基础上建立索引。这类方法包括了GCoding[9]和LsGCoding[14]方法。但是，这些方法提取的结构特征或者缺失环路信息(例如GCoding提取的树形结构)，或者提取的边不包含权值信息(例如LsGCoding只能提取无权边的图谱)，这些都会在处理无向加权边的图数据库时，导致查询的性能降低[14]。

针对无向加权图数据库，G-CORE方法使用路径信息特征，提高了无向加权图的推理和计算的效率[15]。受此启发，本文将加权路径信息和拉普拉斯图谱信息提取出来，按照表示学习方法的思路，提出了无向加权图的子图查询方法PSQuery，来提高无向加权边图集的查询效率。

2 PSQuery编码和索引方法

本文提出的PSQuery方法的处理流程如图1所示。

图1 过滤-验证框架

不同于GCoding和LsGCoding方法，本文将最短权值路径和图谱作为新特征去加速无向加权图的处理过程。首先，对图数据库中每个图的节点、边、最短权值路径和拉普拉斯图谱进行提取，并且将其编码生成数据图码，同时建立索引树和数据图库。接着，对查询图进行编码，生成对应的查询数据图码。然后，按照过滤-验证框架进行查询处理。需要注意的是，PSQuery方法不仅在过滤过程中使用了新的特征编码比较，并且在验证过程中将最短路径信息也作为判定规则，目的是提高方法的整体查询效率。

2.1 图谱及路径的相关性质

定义：(邻接矩阵和Laplacian矩阵)给出一个无向加权图G，其邻接权值矩阵和Laplacian矩阵表示为WG和LG。具体的构成为：

其中，ew为相连节点之间的路径权值。根据上述矩阵的定义，可以计算出图G中的最短权值路径矩阵和对应的图谱信息。

定义：(图谱和Laplacian图谱)给出一个无向加权图G，对应的Laplacian矩阵LG的特征值序列称为G的Laplacian图谱。

对于无向加权图，应用权值路径信息和Laplacian图谱的性质，即路径权值和图谱的嵌套定理可以进行过滤操作[16,17]。

定理：(路径权值的嵌套定理)给出两个无向加权图G1和G2，G1是G2的子图，并且G1中任意两个节点vi和vj，G2中与之对应的节点为v’i和v’j。如果vi和vj之间的最短权值路径为αk，v’i和v’j之间的最短权值路径为α’k，那么它们的路径的权值应满足αk≥α’k。

定理：(图谱的嵌套定理)给出两个无向加权图G1和G2，其Laplacian矩阵分别表示为LAm×m和LBn×n(m≤n)。其中LAm×m的特征值为λm-1≤λm-2≤…≤λ1≤λ0，LBn×n的特征值表示为βn-1≤βn-2≤…≤β1≤β0。如果G1是G2的子图，那么它们的特征值满足λk≤βk，k=0,1,…,m-1。

基于统计学规律，无向加权图中节点标记和边的个数也具有相似的性质，即通过数值比较进行过滤操作。在GCoding和LsGCoding方法中，这两种基本特征已被提取为图的特征编码[9,14]。根据特征进行编码的操作效率高，所以PSQuery提取这4个图属性作为索引特征。

2.2 数据图的编码

本文提取的4个特征包含：节点标记、边、最短权值路径和拉普拉斯图谱。这4个特征编码的组合信息较全面地描述了无向加权图的基本信息、加权路径信息和拓扑信息。

图的编码过程是对每个原始的图数据的节点进行特征提取，生成对应编码；再将每个节点的编码组合生成图的编码。

在编码过程中，提取的第一个特征是节点的标记信息。提取到节点标记信息后，按照哈希映射函数将节点的标记映射到数字空间，生成节点标记编码；然后将所有节点标记编码合并生成图的节点标记编码。

在图2中，Q包含标记为A、C、D的节点各一个，两个标记为B的节点。查找节点哈希函数，v4的节点标记编码为“0001”。对其他节点进行相同的操作，可以得到图中其他节点的标记编码,并且，按位相加即可得到图Q的节点标记编码为“1121”。

图2 节点的哈希映射函数

提取的第二个特征为边信息。通过遍历节点相邻边的哈希映射函数，可以得到邻接边的编码。按位相加可得到图Q的边编码。图3给出图Q中边的哈希映射函数，其中“*”表示经过的任意边权值。

图3 边的哈希函数

对于加权图Q中节点v4的邻接边，通过查找哈希映射函数得到边编码“0100”。最后，将5个节点对应的5个计数串按对应位相加，得到无向加权图Q的边编码为“1331”。

区别于现存的基于表示学习的方法，本文提取路径权值信息和拉普拉斯图谱作为特征进行映射编码。根据路径权值的嵌套定理，可以将两个节点之间的路径权值数进行比较和过滤。本文将最短权值路径作为第三个特征，进行加速过滤操作。在提取最短权值路径时，首先生成邻接权值矩阵，接着针对无向加权图，使用优化的Floyd算法求解各个节点之间的最短权值路径矩阵[18]，如表1所示，其中Ivaule为初始权值。

表1 最短权值路径矩阵的算法(算法1)

通过算法1，由PSQuery方法可以得到最短权值路径矩阵。该矩阵中的元素为节点vi到节点vj的最短权值路径。图2中Q的最短权值路径矩阵为：

根据上述权值矩阵，PSQuery方法通过将矩阵中的元素进行编码，并且进行计算，得到每个节点到标记为L′节点的最短权值路径；再取每个节点的权值中的最小值作为图Q的权值路径编码。图4给出了权值路径编码的生成过程。

图4 图Q的权值路径编码

PSQuery方法提取的最后一个特征为Laplacian图谱。具体生成过程中，对每个节点生成L(为一整数)层生成图，并且计算对应图谱来表示各个节点的局部拓扑信息；再将节点的图谱进行组合，得到整个无向加权图的拓扑信息，即Laplacian图谱。其中，L层生成图的算法如表2所示。

表2 L层生成图的生成算法(算法2)

按照算法2，PSQuery可以生成节点L层生成图；接着，按照雅克比算法求解出对应的特征值，并取最大的两个特征值作为节点的图谱；最后，将所有节点的图谱组合，生成图的Laplacian图谱。

根据上述提取特征和对特征进行编码的过程，可以得到节点编码和图编码，具体如图5所示。

图5 节点编码和图编码

2.3 索引的建立

索引树的构建参照GCoding方法中索引树的构造过程[9]。使用图编码中节点标记编码和边编码作为索引树的一个节点。下面给出4个数据图的索引树实例。

在图6(a)中，列出的图数据库包含了图G1、G2、G3和G4。图6(b)为该图库的索引树。PSQuery方法提取每张数据图编码中的前两部分作为索引的特征，构建索引树。

图6 索引树

在构建索引树的过程中，对于具有相同节点标记编码V和边编码E的无向加权图，将其作为同一个叶子节点进行处理。其中，每个中间节点有l(l为整数)个孩子节点，且中间节点C0、C1、C2、…、Cl的编码为l个孩子节点的编码值中对应位上的最大值。同时，按照平衡树的生成方法，将每个图的编码插入索引中，最终得到一个完整的平衡索引树[19]。

3 PSQuery的查询处理

3.1 过滤过程

本文所提方法中过滤规则分为两部分：节点过滤规则和图过滤规则。具体地，先根据图过滤规则，筛选出初步符合条件的无向加权数据图集，再对这些数据图集使用节点过滤规则进行二次过滤，找出真正符合条件的候选图集。下面具体给出两个过滤规则。

图过滤规则：给定两个无向加权图G1和G2，G1包含m个节点，G2包含n个节点。其中n≥m。假定它们的图编码分别为gCode(G1)=〈V(G1),E(G1),P(G1),L(G1)〉和gCode(G2)=〈V(G2),E(G2),P(G2),L(G2)〉(其中P为最短权值路径编码，L为拉普拉斯图谱)。若G1和G2的图编码不满足下列条件：

①V(G1)[i]=V(G2)[i],i=0,1,…,lV-1;

②E(G1)[i]≤E(G2)[i],i=0,1,…,lE-1;

③P(G1)[i]≥P(G2)[i],i=0,1,…,lV-1;

④L(G1)k[i]≤L(G2)k[i],i=0,1，k=0,1,…,m-1。

那么G1不是G2的子图。

节点过滤规则：给定两个无向加权图G1和G2，对于G1中的任一节点v，其编码为〈V(v),E(v),P(v),L(v)〉。如果无向加权图G2中找不到这样的节点v′，其编码对应表示为〈V(v′),E(v′),P(v′),L(v′)〉，且满足以下条件：

那么G1不是G2的子图。

由于图过滤规则的效率高于节点过滤规则，PSQuery方法首先使用图过滤规则遍历索引树，接着使用节点过滤规则进行判定，生成规模较小的候选集。

以图2中的查询图Q为例，使用图过滤规则遍历图6中的索引树。首先将Q的图编码与根节点进行比较，发现不满足图过滤条件，继续遍历其孩子节点；当遍历到中间节点C2，对比编码E时，满足图过滤规则，则C2及其孩子节点全部删除。同理，遍历到G1时也满足图过滤规则，也被删除，最后产生候选集为{G2}。按照同样的判定方法，经过节点判定规则后，就可以生成最终的候选集合。

完成过滤后，接着对每个候选图进行验证处理，得到最终的查询结果集。

3.2 验证过程

在验证阶段，采用经典的VF2算法进行子图同构的判定[20]。在VF2方法中，对匹配对进行判定的可行性规则由两部分组成：语法规则和语义规则。语法规则按照VF2算法中列举的相关规则进行判定。对于语义规则，VF2算法根据子图中节点和邻接边与超图中对应节点和对应邻接边的相似匹配关系进行判定。为了实现无向加权图中加权边的信息判定，在验证过程中，将节点过滤规则也作为语义规则的一部分进行判定，从而加速了无向加权图的同构判定效率。

4 实验结果和分析

4.1 数据源

为了进一步验证所提方法的可行性和有效性，本文选取第三类基于表示学习的GCoding和LsGCoding方法进行比较和验证。在具体的实验中，对比的两种方法均基于iGraph框架进行编程实现[21]。

这三种方法都提取了节点和边的信息，而实验性能差异主要是由于GCoding方法将生成子树的图谱作为该方法的主要特征，LsGCoding方法将生成子图的图谱作为主要特征，而PSQuery方法将生成子图的拉普拉斯图谱和最短路径长度作为主要特征所导致的。由于主要特征的不同，这三个方法在过滤和验证过程中的过滤和判定效率不同，本节内容是对这三种方法的性能测试。

实验中的输入数据分为两类数据：真实数据集和合成数据集。

1)真实数据集。该数据集包含10 000个简单数据图作为测试数据图集，是从Developmental Therapeutics Program主页上已知分类的化学分子式中提取出来的，并且大部分子图查询方法均采用该数据集进行测试。其中每个图的平均节点个数为25.4，边的个数为27.3。输入的查询图集也来源于这个真实数据集，包括了6个查询集合：Q4、Q8、Q12、Q16、Q20、Q24，其中每个查询集Qi包含了1 000个随机抽取的查询图，并且边的个数为i。

2)合成数据集。合成数据集由iGraph提供，使用图生成器GraphGen生成。此数据集包含10 000个稠密数据图，数据集中图的平均节点个数为30，边的平均密度为0.5。查询图集则按照真实数据集的抽取方式进行抽取，同样得到Q4、Q8、Q12、Q16、Q20、Q24，一共6组数据集。

4.2 参数设置和实验环境

在实验中，测试3种方法，其中每种方法的参数设置主要涉及提取图谱时构造的节点对应的N层生成图或者树的层数，以及最终生成图谱时选取的特征值的个数。这两个参数选用与GCoding相同的两个参数值，即N=2，特征值个数等于2。这是因为在iGraph框架中，通过实验发现，当N大于2或特征值个数大于2时，候选集的大小不会发生太大变化。

实验的运行环境为Windows XP SP3系统，CPU为Intel Core CPUI7-8550U，内存大小为3.5G，开发环境为Visual Studio 2010。

4.3 结果评测标准

实验包含两大部分：生成编码，构建索引树的过程和查询处理过程，所以评判标准也分为两个部分。评判标准1为索引的构建时间和索引的大小；评判标准2为候选集的大小和查询时间。对应的评判结论为：构建索引和编码的时间越少，并且索引树越小，说明方法性能越好；候选集越小，查询时间越短，说明方法的查询性能越好。

4.4 实验结果与分析

实验中，从10 000张真实或合成数据图中随机抽取4次，对应图数量分别为2 000、4 000、6 000、8 000张，加上10 000张数据图，形成5种规模的数据集。针对这5个不同规模的数据集，分别进行编码，构建索引和查询处理的操作，得到图7～图10所示的真实数据集上的实验对比结果，以及图11～图14的合成数据集上的实验对比结果。

1)真实数据集上的结果分析。

图7 真实数据集上编码和索引时间

图7展示了真实数据图库规模从2 000张到10 000张图时，3种方法的编码和索引时间。PSQuery方法提取节点和边信息、权值路径和Laplacian图谱，而GCoding和LsGCoding方法只有节点、边和图谱(或者拉普拉斯图谱)信息，所以PSQuery方法编码和索引构建的时间大于GCoding方法和LsGCoding方法。

图8 真实数据集上索引的大小

图8展示了真实数据图库从2 000张到10 000张图时，编码和索引大小的实验性能。因为PSQuery方法比GCoding和LsGCoding方法提取的特征多了权值路径信息，所以PSQuery方法中数据图库和索引所占空间更大。而GCoding方法的主要特征只有子树的特征值，所以GCoding方法的索引空间最小。

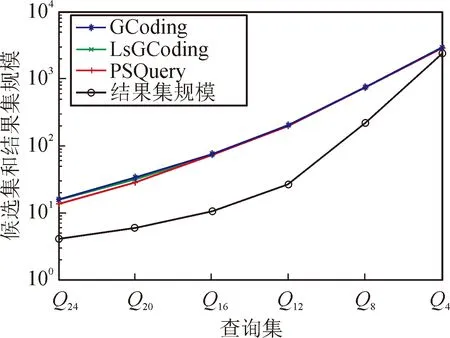
图9 真实数据集候选图集合的大小

图9为真实数据库中不同查询图集合下，3种方法过滤后的候选集的大小。随着查询图集合从Q24变化到Q4，3种方法的结果集在增大，候选图集也在增大。与GCoding和LsGCoding两个方法相比，由于PSQuery方法提取更多的权值路径信息，其裁剪过滤性能最好，所以在真实数据集上，PSQuery方法生成的候选集最小。由于候选集规模直接影响查询效率，所以这也说明PSQuery方法在一定程度上提升了过滤的性能。

从图10中可以看出，随着真实数据集上查询图从Q24变化到Q4，3种方法的查询时间都在增大。这是因为候选集一直在增大，必须花费更多的时间去进行子图的验证操作才能得到最终结果集。并且除了Q4，PSQuery方法的查询时间均小于GCoding方法和LsGCoding方法。由于提取了更好的图特征，PSQuery方法候选集最小，验证时间最少，相应的查询时间最少，这说明PSQuery方法提高了真实数据集上的加权无向图的子图查询效率。

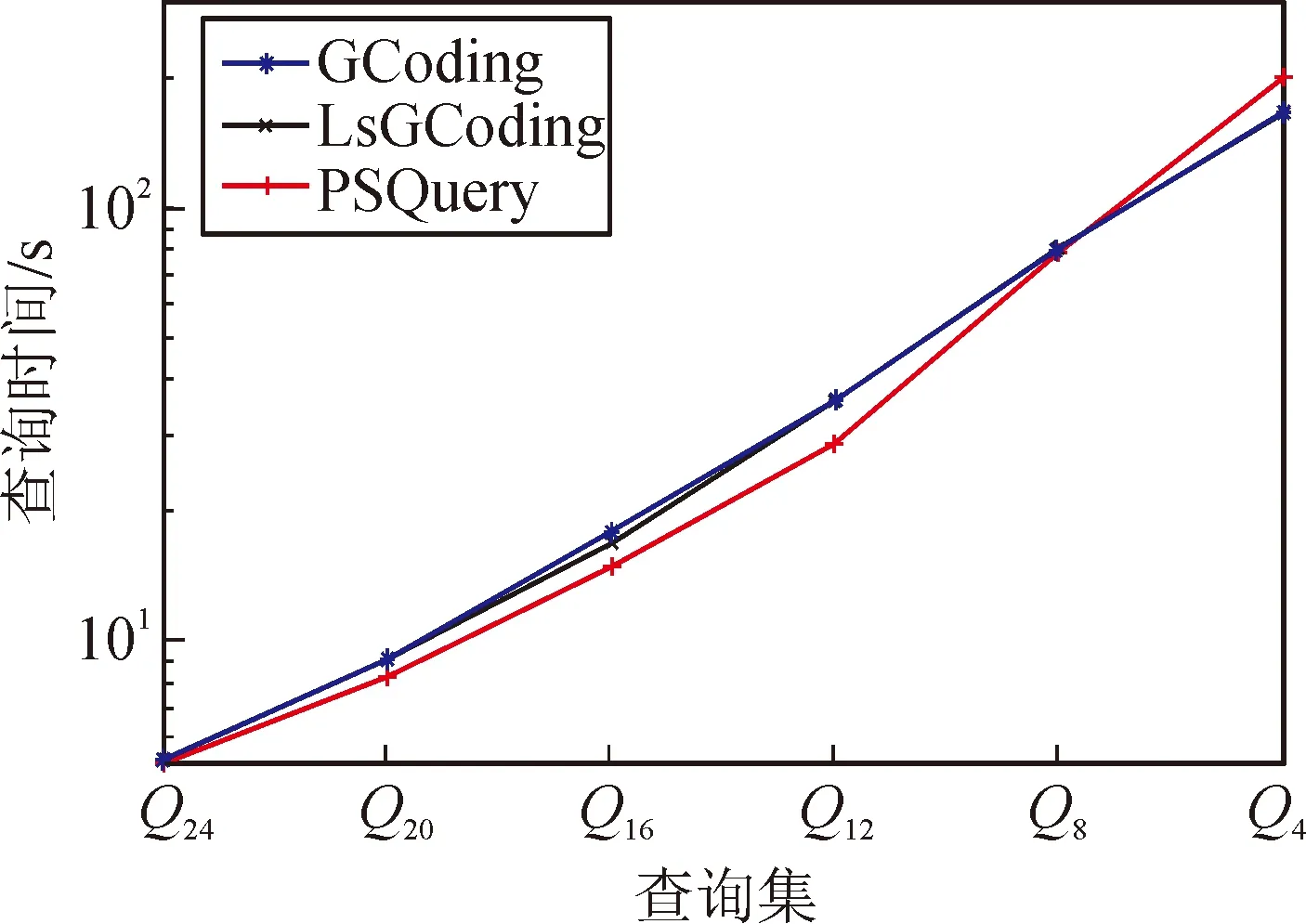
图10 真实数据集上的查询时间

2)合成数据集上的结果分析。

图11 合成数据集上编码和索引时间

图11给出了3种方法在合成数据集上的编码和索引时间。相较于LsGCoding和PSQuery方法，GCoding方法的编码和索引时间最大。这是因为合成图大部分为稠密图，针对稠密图，GCoding方法在生成N层生成树时会增加多个重复的节点，因此对应的邻接矩阵在计算特征值时会十分复杂[14]。由于PSQuery方法相较于LsGCoding方法，增加了路径的权值信息，所以花费的时间多于LsGCoding方法。

图12给出了3种方法在不同合成数据集规模上的索引大小。因为PSQuery方法提取的特征多于GCoding和LsGCoding方法，所以PSQuery方法的索引所占空间最大。

图13给出了合成数据集上3种方法在不同规模查询集上的候选集大小。随着查询集的边个数递减，3种方法在合成数据集上的候选集在增大。并且稠密图中，节点和边的基本信息可以覆盖部分权值路径信息，所以在不同查询集上，3种方法的候选集规模很接近，裁剪后的过滤性能近似相同。

图12 合成数据集上索引的大小

图13 合成数据集候选图集合的大小

图14 合成数据集上的查询时间

图14给出了合成数据集上不同查询集的查询性能。当查询集从Q24变化到Q4时，LsGCoding方法的查询时间少于GCoding方法。而PSQuery方法提取了权值路径信息，其产生的候选图集最小，所以其查询时间均小于GCoding和LsGCoding方法。

从真实数据和合成数据的实验结果可知，在编码和索引阶段，PSQuery方法的索引时间和所占空间均大于GCoding和LsGCoding方法。但是在加权无向图的多次子图查询处理过程中，索引只需建立一次，所以索引相关操作并不能作为主要的性能评定指标。而每次查询都会产生的查询时间是其主要的性能评定指标。从真实数据集和合成数据集的查询性能上分析，PSQuery方法产生的候选集规模最小或者相似，并且验证过程中增加了权值的判定条件，所以PSQuery方法的查询时间都优于同类其他方法，从而在一定程度上提高了加权图的子图查询效率。

3)数据集更新时的性能分析。

数据集更新的操作主要是对图数据集合进行添加操作。针对数据图集合的添加，使用GCoding方法提到的数据更新性能分析方法，对真实数据集，在数据集规模为2 000的基础上，每次增加2 000个数据图进行更新性能分析[9]。同样，选择经典的基于频繁子结构方法gIndex与PSQuery方法进行比较[9]。

基于表示学习的方法，在计算新插入数据图的特征编码的基础上，将其编码插入到索引树中，这样便完成了更新操作。但是，对于基于频繁子结构的方法的图更新处理，现存的处理方法有两种机制：①直接将新加入的数据图进行处理，只是在倒排索引中增加新图的ID；②将新加入的图和原数据集重新开始进行频繁子结构挖据，新建整个倒排索引[13]。所以，在该部分实验中，将PSQuery方法的更新操作和gIndex方法的两种操作进行比较。

还有一个数据集更新时的评价指标：索引构建时间，用于描述编码的索引更新的时间。索引构建时间越少，说明更新的代价越小，适应数据集更新的性能就越好。图15～16为过滤效率的实验结果。

图15 数据集更新时的裁剪效率

在图15中，PSQuery方法在数据集每次增加2 000个图集的情况下，裁剪的效率性能比较稳定。gIndex方法的新建索引的裁剪效率也比较稳定，但是该方法在增量构建索引的情况下，其裁剪效率明显在下降。

图16 数据集更新时索引构建时间

在图16中，随着更新数据集的增大，PSQuery方法和gIndex方法构建索引的时间都在增大。对于gIndex方法，其增量形式构建索引方法的花费时间虽然较小，但是图16中该机制下索引的裁剪效率在降低，进而降低该方法的查询效率。而gIndex如果每次新建索引，其索引构建时间会大幅增大，而其裁剪效率变化不是很大，略低于PSQuery方法。PSQuery方法在数据集更新的情况下，索引构建时间和裁剪效率相较于gIndex方法的两种不同机制都比较稳定。所以PSQuery方法可以很好地处理数据集更新的情况。

5 结 语

本文针对无向加权图的子图查询问题，提出了基于最短权值路径和Laplacian图谱的新编码方法，并且在编码的基础上生成了新的索引树。同时，按照过滤-验证框架进行子图查询，通过大量的实验证实了该方法具有一定的可行性和有效性，特别是PSQuery方法可以很好地处理数据集更新的情况。后期计划将这些新编码应用到超图查询和知识图谱的查询问题中，并且寻找更优的图特征去处理有向图的查询问题。