基于深度信念网络的信用评估研究

1.华南师范大学数学科学学院，广东广州 510631

2.华南师范大学金融工程与风险管理研究所，广东广州 510631

引言

2018年，以土耳其、阿根廷为代表的几个新兴市场国家轮番遭遇到货币贬值的危机，一度让人开始担心 1998年金融危机再现。表面上，美国对这些国家开打贸易战是造成上述情况的直接原因，但究其深层次原因还是在于这些国家自身，其中一个重要因素是它们各自过高的外债比例(如土耳其货币危机爆发时其外债规模已占到本国 GDP的52%)，一旦经济环境出现不利变化，极易导致信用风险的急剧增加，且该状况会迅速向企业、金融机构、投资者蔓延，给金融市场带来极大冲击，最终可能导致金融危机的爆发。反观历次金融危机的产生基本上都离不开信用风险恶化这个重要根源。显然，信用风险的评估与防范对金融监管当局及相关金融机构、投资者等而言是至关重要的。

1 相关文献

由于信用风险的复杂性，信用风险评估的模型也多种多样，但从技术方法角度来看，主要可分为两类基本模型(Chen et al，2016)：一类是以统计分析为基础的模型；另一类则是基于智能技术方法构建的模型。前者典型代表包括线性判别分析法、二次判别分析以及 logistic 回归模型等；后者包括了现今比较流行的一些机器学习方法，主要有神经网络(NN)、决策树(DT)、进化方法、模糊逻辑(FL)以及支持向量机(SVM)等。Prado 等人(2016)利用 Web Science 数据库，采用文献计量方法分析了从 1968到2014年间所发表的有关信用风险和破产研究的期刊文献，他们对比了研究者使用这两类模型情况，发现虽然判别模型和logistic 模型一直是研究者常用的方法，但从上世纪 90年代以来，以神经网络为代表的人工智能技术得到越来越广泛的运用，一个重要原因是后者不像前者需要严格假设前提，而且在处理非线性、病结构问题方面比前者有更明显的优势，因此在面对日益复杂的信用风险，基于后者的评估模型也越来越受到相关研究人员的青睐，并在这方面取得了不少的研究成果。Blanco 等人(2013)运用多层感知器(MLP)神经网络模型构建企业信用评分模型，以误判成本为标准，对比线性判别(LDA)及 logistic 等统计模型，发现神经网络模型结果要优于统计模型；Korol(2013)则将神经网络运用在对比中欧地区和拉美地区的企业在破产风险预测上的不同；Khashman(2011)也通过神经网络技术构建信用风险的评价模型；杨淑娥等(2007)则利用 BP 神经网络(BPNN)构建了我国上市公司财务预警模型，并在实际运用中得到了较好的结果；Wang 等人(2012)、Sun 等人(2012)在进行公司信用评估预测研究中则采用了SVM方法并取得了较好的效果。Yao 等(2015)则将 SVM 成功地运用在公司债券违约损失的预测上。

然而上述模型在使用过程中缺陷也很明显，如BP 神经网络为例，存在局部最优、泛化性较差的缺点，究其原因，一个重要因素是传统神经网络(包括支持向量机等)为代表的这类模型本质上是一种浅层学习结构(即网络结构层次较少，如普通神经网络一般只包含一个隐层)，当遇到高维、数据量庞大、结构复杂的数据问题时，这类浅层结构算法在刻画数据特征、表达复杂函数方面的能力就非常有限了；但若采用多层网络结构，系统复杂性自然增大，采用传统的神经网络算法(如 BP 算法)，又会出现梯度消失或梯度爆炸问题，实际运用中还会产生严重的过拟合问题。基于此，Hinton 等人(2006a，2006b)提出了深度学习的思想来克服上述缺陷，其主要观点为：1)采用多隐层的深层网络结构相比浅层结构更能学习刻画复杂数据的本质特征，对可视化和分类等任务而言有很大的帮助；2)通过无监督的通过逐层初始化(layer-wise pre-training)策略来有效克服深度神经网络在训练上的困难。由于深度学习在处理复杂数据中体现出的优异性能使其一问世便受到许多研究者的关注和重视。近年来，深度学习已经在图像分类、多媒体检索、交通流预测、语音处理及疾病诊断等许多领域得到广泛的运用，并且取得了较传统方法更优的效果(焦李成等，2016)。由于金融市场数据有复杂的非线性特征，因此有研究者借鉴其他领域的成功经验，将深度学习引入到金融领域研究中，如 Shen等(2015)、曾志平等(2017)运用深度信念网络(Deep Belief Networks，DBN)方法分别对汇率和股票走势特征进行分析和预测；而 Luo 等人(2017)使用信用违约互换(CDS)数据对比了深度信念网络(DBN)模型与logistic 回归、多层感知器以及 SVM 模型的信用评分效果，发现DBN 效果最好；Kvamme 等(2018)则利用深度卷积神经网络对抵押贷款的违约进行预测。目前，深度学习在金融领域当中的应用和研究主要集中在金融市场运动的预测及相关交易策略的改进与决策分析等方面(苏治等，2017)，在公司信用评估方面的研究还是比较少的。鉴于上述分析，特别的，由于深度信念网络优异的对数据本质特征学习和刻画能力以及在其他领域的成功运用，本文提出一种基于深度信念网络的信用评估研究模型，并将其运用在中国和美国上市公司的信用评估实践中。

2 深度信念网络评估模型

深度信念网络(DBN)是运用较广的一种深度学习模型。DBN 由若干个叠加的受限玻尔兹曼机(Restricted Boltzmann Machines，RBM)和一个BP 神经网络构成，其网络结构类似于多层神经网络结构，但在训练算法上，DBN 采用了无监督的逐层训练方法，克服了传统的多层神经网络很难运用梯度下降算法进行训练的缺陷。由于DBN的主要构成基础是RBM，这里首先介绍RBM，在此基础上再介绍DBN的具体结构和训练算法。

2.1 受限玻尔兹曼机

受限玻尔兹曼机(RBM)可被看成是一个二分无向图模型，如图1所示。V为可视层，含m个神经元(节点)，代表输入数据；H为隐含层，含n个神经元，目的是对输入数据进行特征提取，W为可视层与隐含层之间对称的连接权重。并假设所有节点都是随机二值变量节点(取 0 或 1)，全概率分布p(v，h)满足Boltzmann 分布。则 RBM的能量函数定义为：

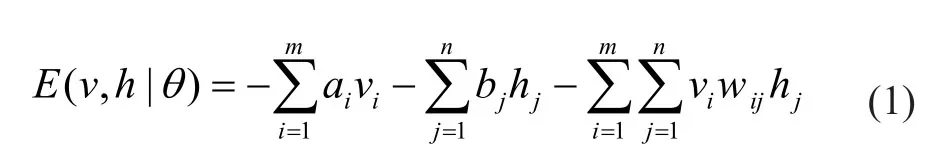
其中，Wij为可视层节点i与隐含层节点j之间的连接权重，ai为i的偏置，bi为j的偏置，θ={Wij，ai，bi} 代表RBM 中所有的参数集，当确定时，根据式(1)易得的联合分布概率为：

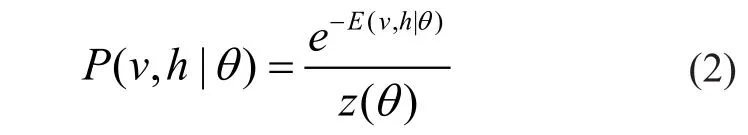
其中，z(θ)=Σv,he-E(v,h|θ)是配分函数，起归一化因子的作用。因此，对(2)取边缘分布，可得 RBM的可视向量分布和隐含向量分布分别为：

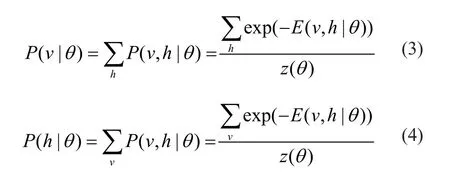
图1 受限玻尔兹曼机(RBM)结构示意图Fig.1 Schematic diagram of the restricted Boltzmann machine

根据 RBM 结构可知，可视层和隐含层各节点的激活状态是相互独立的，可知在给定可视层向量v时隐含层节点j的条件概率以及给定隐含层向量h时可视层节点i的条件概率分别为：

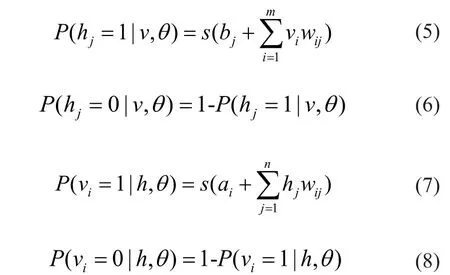
其中，为sigmoid 函数，即：

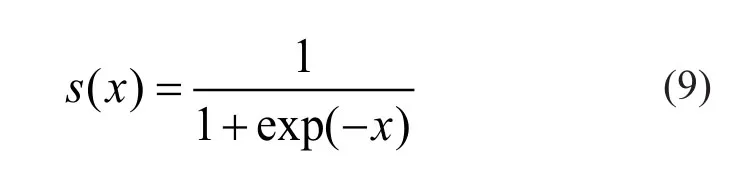
从上分析可看出。RBM 实际上就是一种随机神经网络，其训练是通过迭代方式完成，训练学习的目的就是确定参数θ={wij,ai,bj}的合适值。RBM 一般使用最大似然估计来找到其隐含层中输入的随机表达式(潜在特征)，即通过最大似然函数推导参数θ的更新公式。参数的更新迭代公式为：

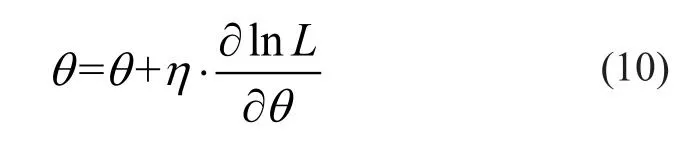
其中，η为学习率。上述迭代理论上可采用梯度下降算法来实现，但实际上梯度很难计算。因此文献(Hinton，2006)提出了一种对比分歧(contrastive divergence，CD)方法来得到各具体参数的更新公式。对比分歧法是首先通过一步完全 Gibbs 采样，利用式(5)更新所有隐含层节点h，随后再由式(7)更新所有可视层节点得到v’，最后再次通过式(5)得到h’。故各参数更新规则可由如下公式给出：

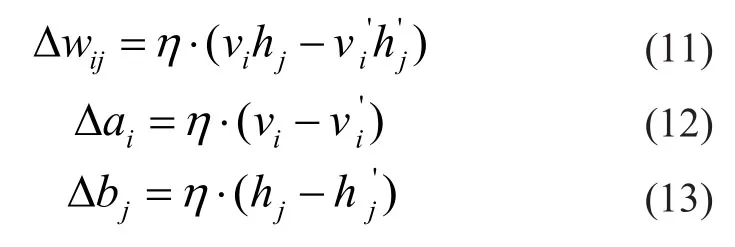
2.2 深度信念网络及训练算法

2.2.1 模型结构

深度信念网络(DBN)是由若干个RBM堆叠而成的多层信念网络，图2为拥有三个隐含层的DBN的拓扑结构示意图，为简洁起见，连接权重W及偏置a和b并未在图上标示出来:

在上述DBN 结构图中，第一个RBM(即RBM1)将输入作为可视层，其隐含层可被看成是第二个RBM(即 RBM2)的可视层，RBM2 将学习 RBM1的隐含层中的特征输出，并将该输出作为下一层的输入，依次类推，每一层从前一隐含层中学习抽象出其包含的特征分布，而 RBM1的输入是整个网络模型的输入，这样通过网络的不断堆叠，模型能够逐层学习提取出原始数据中更复杂、更深层次的数据特征。而在顶层的BP 网络则利用提取的数据特征为输入，进行分类或评估预测。

2.2.2 模型训练算法

由于信用评估本质上可以看成是一种判别分类问题，将DBN 用于信用评估过程中，其充当就是一种判别模型角色。然而，DBN 是一个具有多隐含层的深度神经网络模型，其权值参数的训练是一个非常困难的任务，若直接采用传统的梯度算法(如 BP 算法)来训练参数，会使模型极易陷入局部最优，另外，随着深度的增加，梯度的幅度会急剧减小，导致浅层(靠近输入层)神经元(节点)权值参数难以更新，无法有效学习。鉴于此，DBN的判别学习过程分为两个阶段来克服上述缺陷：首先利用 RBM 进行逐层无监督预训练，然后再利用 BP 反向传播算法进行有监督的调优，具体过程如下所述。

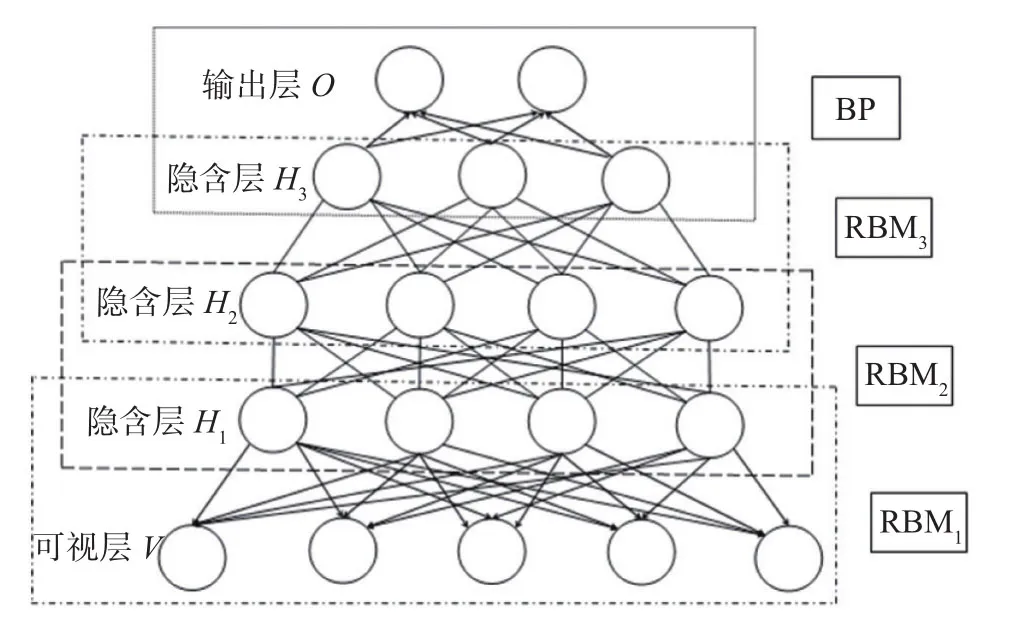
图2 深度信念网络(DBN)的拓扑结构示意图Fig.2 Schematic diagram of the topology of the deep belief network

第一阶段：利用无监督的贪心逐层训练算法对网络权值等参数进行预处理。最开始先对 RBM1 进行训练(具体训练算法可采用前面所述的对比分歧算法)，然后保存训练好的RBM1的权值和偏置，将 RBM1 隐含层的输出作为RBM2的输入，接着同样方法对 RBM2 进行训练，依次类推，分别对所有的RBM 进行训练，实现了对DBN 网络权值的预处理。这种操作可以降低采样噪声，更有利于加快网络的学习速度，这一阶段又被称为预训练阶段(pre-training)。通过无监督的贪心逐层训练算法，能够有效地对网络权值进行预处理，使权值参数获得一个较优的值。该算法虽然有效，但所求权值并非最优，因此往往需要根据实际问题进行进一步微调。

第二阶段：微调(fine-tune)阶段，亦称调优阶段。这一阶段是采用 BP 算法对整个网络参数进行调整，即在预训练结束之后，处在最后的RBM的输出作为顶层 BP 网络的输入，此时整个网络参数已确定(相当于已预先设定好了网络的初始参数)，然后利用带标签的训练样本通过 BP 算法对整个DBN 网络权值参数进行调整，直到停止条件满足为止。

实际上，预训练+微调的做法可看作是将许多参数分组，对每组先各自找到局部比较好的位置，然后再基于这些局部较优的初步结果看成一个整体，从总体上对其进行全局寻优。这样做的结果大大提高了模型的学习能力，改善了模型的泛化能力，提高了其评估预测的效果。基于DBN 模型的整个信用评估框架如图3所示。

3 模型在信用评估中的应用

3.1 样本数据来源及指标选择

3.1.1 样本数据来源

本文选取了我国上市公司数据和在美国上市的公司数据两个公开样本数据集，其中我国公司数据来源于wind、同花顺财经数据库及同花顺iFinD 数据库，美国公司数据来源于compustat 数据库。

我国上市公司数据样本是从 2000至2014年被宣布实施 ST的公司中(剔出金融行业以及由于财务作假或非财务原因被 ST的)选取共 300 家 ST 公司，另外选取同时期的非 ST 公司样本 1200 家，共计 1500个样本公司构成*(数据来源于Wind 数据库、深圳国泰安 CSMAR 数据库和同花顺 iFinD 数据库)。假定公司t年被宣布 ST，由于公司t年被宣布 ST和该公司公布t-1年度财务报表几乎是同时发生的，故本文采用了t-2年的数据来预测t年是否会被 ST，例如 2012年被宣布 ST的公司，则采用2010年财务数据来进行分析。即中国公司样本数据共 1500个，其中信用状况为好的1200个，为差的300个；

类似，美国公司数据样本也是从 2000至2014年被标普公司评级过的公司中选取了 1704个样本公司，美国公司被评级范围从 AAA到D 共 10个等级(分别为AAA、AA、A、BBB、BB、B、CCC、CC、C和D，其中AA至CCC 级可用“+”和“-”号进行微调)，为简单起见，我们将美国上市公司也分为好和差两类，评级在AAA+至B-的被视为信用较好企业，评级在CCC+到D的被视为信用较差企业。这样在1704个样本中，基于上述分类，被归为信用好的样本为1549个，差的为155个。

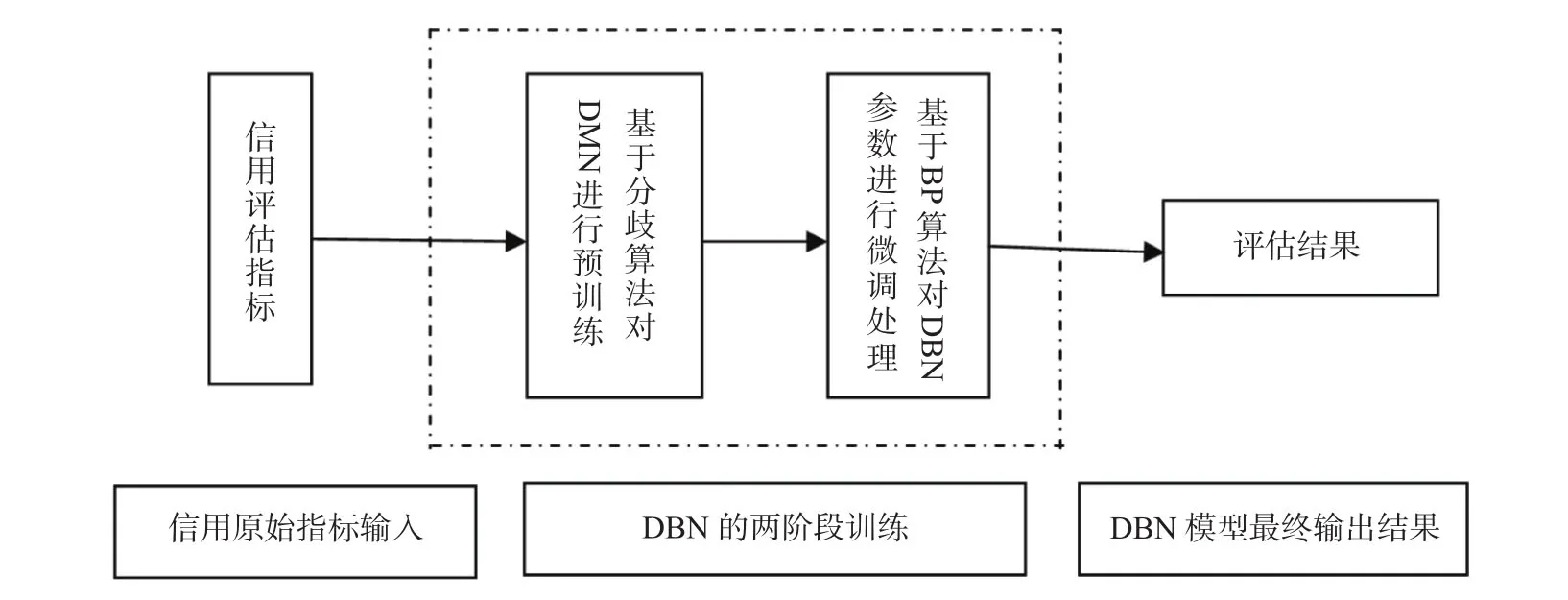
图3 基于DBN 模型的信用评估框架示意图Fig.3 Schematic diagram of credit evaluation framework based onDBN model

我们将这两个数据集随机划分为训练集和测试集，训练集与测试集样本数量比例关系大体为65:35，具体来说，中国公司样本训练集包含 975个样本(占样本总数的65%)，其中信用类别为好的790个，为差的185个；测试样本集为525个样本(占样本总数的35%)，其中信用为好的410个，为差的115个。美国公司训练集为1107个样本(占样本总数的64.96%)，其中信用类别为好的1012个，为差的95个；测试样本集为597个样本(占样本总数的35.04%)，其中信用为好的537个，为差的60个。

3.1.2 指标选择及模型参数选取

本研究在深入分析公司财务报表结构的基础上，结合前人的研究，从偿债能力、营运能力、盈利能力、现金流量及发展能力等方面分析整理了 40个指标，具体见表1所示。

由于上述指标之间可能存在高度相关性，本研究基于相关系数的变量选择方法(这里采用了逐步回归选择法)分别对中美公司样本指标进行变量筛选，限于篇幅，具体筛选过程就不再赘述(更详细的介绍可参看文献[Falangis et al，2010])，最后筛选结果如下：中国公司样本指标共筛选出 10个指标，分别是X3，X5，X8，X14，X16，X24，X25，X27，X33和X36；相应的，美国公司样本指标共筛选出 13个指标，分别是X1，X8，X9，X10，X13，X18，X21，X24，X26，X29，X33，X34和X40。由于这两个样本集的信用评估分析过程基本相同，这里以中国公司样本集为例来说明基于DBN的信用评估模型的构建过程。

首先对原始指标数据做了归一化处理，归一化函数如式（14）所示：

表1 输入指标名称一览表Table1 Enter indicator name list

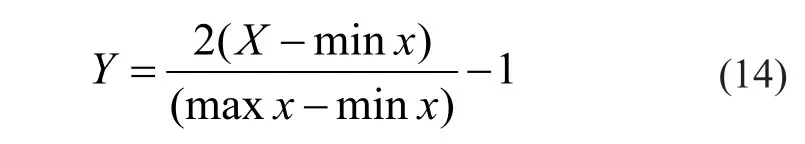
这里，X代表输入矩阵，maxx和minx分别为X中的最大和最小值，使得输入向量的值量化到[-1，1]内。DBN 模型的构建是基于darch 软件包(Package for Deep Architectures and Restricted Boltzmann Machines)通过 R 语言编程实现。由上述分析可知，该网络模型的输入层节点为10；预训练阶段学习率η1=0.001，精调阶段学习率η2=0.001，隐含层数及每个隐含层节点数通过试错法确定，分别对隐含层数为2、3、4、5 以及隐含层节点数为10、20、30、40 时的共 16 种结构进行训练对比，最终确定采用 3个隐含层结构，每个隐含层节点数为30的网络结构，因此，该模型结构为一个10-30-30-30-1的网络结构；其中，预训练阶段学习率η1=0.001，精调阶段学习率η2=0.001，其它参数为darch 包中的默认参数，输出变量为单变量y，即输出层为一个节点，若y=1 则代表信用差(ST 公司)，y=0 则代表信用好(非 ST 公司)。

3.2 实证研究结果

一般来讲，模型的检验是用对训练样本和测试样本中分类的判定准确度来表示，尤其是对训练样本外的测试样本中的判定准确度更能反映模型的泛化性和预测性。故本研究采用I类错误率、II 类错误率和总误判率三个指标作为衡量模型预测准确度的标准。这里第一类错误指的是将高信用风险(信用差)公司误判为低信用风险(信用好)公司，即将 ST 公司判为非 ST 公司；第二类错误指的是将低信用风险(信用好)公司误判为高信用风险(信用好)公司，即将非ST 公司判为ST 公司；总误判率指所有被错判的公司数与样本公司总数的比值。此外，为对比分析，本研究还利用前面文献所提到的一些经典方法，包括 BPNN、Logistic 回归、SVM、DT(采用 C5.0 算法)及 LDA 等构建了相应的信用评估模型，表2为所构建的六种模型对中国上市公司测试样本集的预测结果。

从表2 可看出，所构建的六种模型对测试样本集的预测结果总体来看都相当不错，其中总误判率最高的为DT 模型，误判率为8.57%，最低为DBN 模型，误判率仅为4.38%；从 I 类错误率指标来看，最高仍为DT 模型，误判率达到22.41%，而最低为DBN，只有 13.04%，差不多只有 DT 模型的一半；再看 II类错误率，最高为LDA 模型，其误判率为4.89%，最低还是DBN 模型，仅为1.95%；另外，我们对美国公司样本也做了类似地分析研究，表3为六种模型对美国公司测试样本集的预测结果。

同样地，从表3 结果可看出，I 类错误率最高为DT 模型的23.33%，II 类错误率最高则为LDA 模型的5.96%，总误判率最高为LDA 模型的6.53%；而DBN 模型在上述三个指标的结果分别为10.00%、2.05%和2.85%，表现是最好的。综上可看出，无论是中国公司样本集还是美国公司样本集，从 I 类错误率、II 类错误率及总误判率这三个指标的表现来看，基于DBN 模型的信用评估预测效果都要远优于其它五种模型的评估效果，这也说明本研究所构建的DBN 模型相比其他传统模型的确能更好地挖掘和刻画出复杂数据背后的特征关系，从而大大提高模型预测的准确性和可靠性。

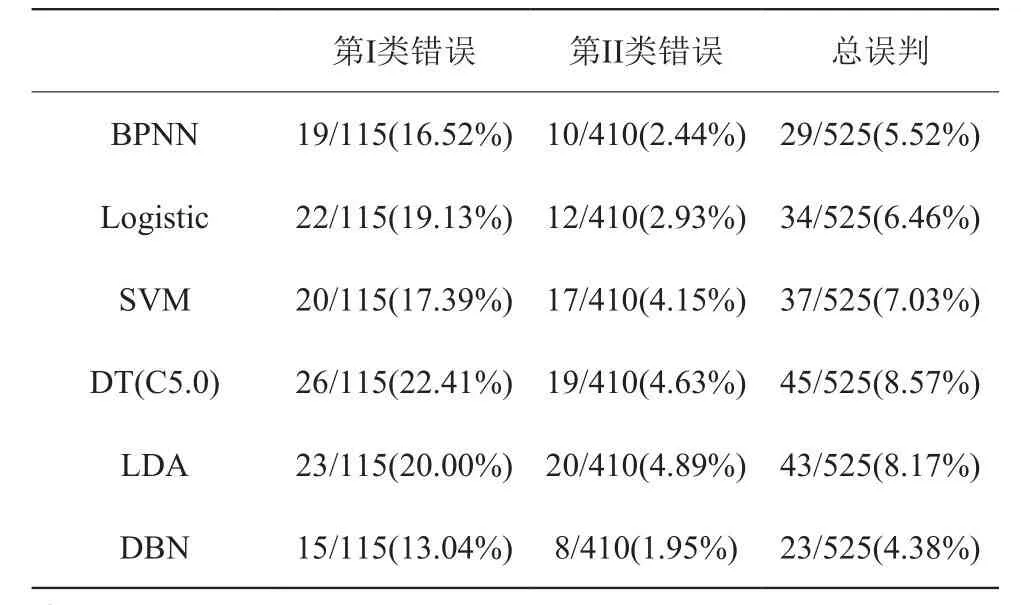
表2 六种模型对中国上市公司测试样本的预测误判结果对比Table2 Comparison of prediction results of six models on test samples of listed companies in China

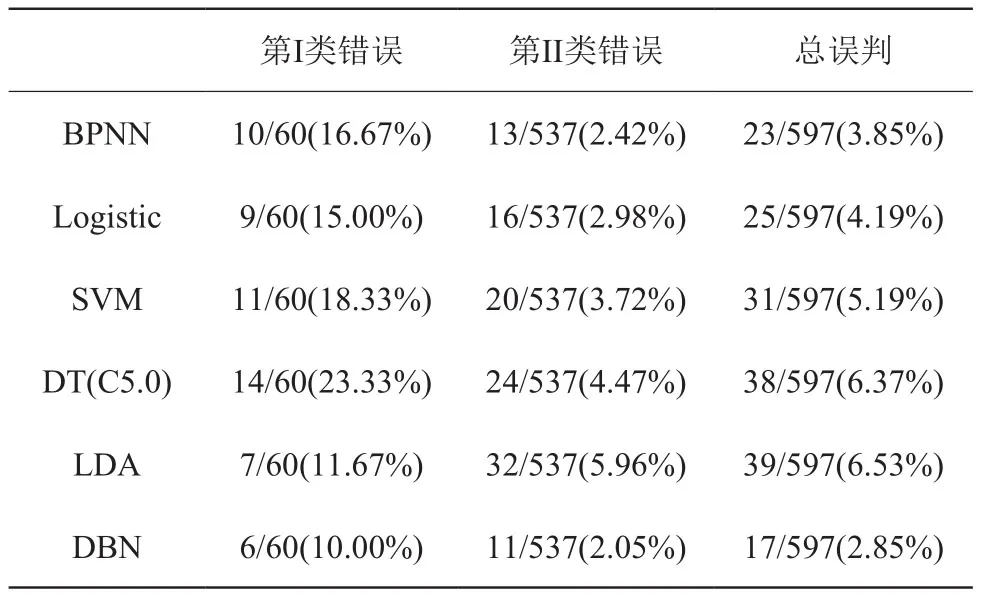
表3 六种模型对美国公司测试样本的预测误判结果对比Table3 Comparison of prediction results of six models for US company test samples

4 结束语

传统的信用评估模型对信用风险的高维性、非线性等特点处理起来比较困难，在实际运用中往往存在较大误差，极大影响评估效果。深度学习作为当前新兴的一种人工智能学习算法，由于其在处理复杂问题、刻画非线性数据特征方面具有其他方法不可比拟的优势，已经受到各方面广泛关注，并取得不错的应用效果。鉴于此，本研究在分析深度学习算法的基础上，首先通过变量选择方法将高维信用变量降维，然后采用深度信念神经网络(DBN)构建了基于DBN的信用评估模型。通过在两个公开样本集（中国公司样本集和美国公司样本集）的实际验证，相比其它 5个经典模型，实证结果显示，基于DBN的信用评估模型在I 类错误率、II 类错误率和总误判率三个指标上都要好于其它 5 种对比模型，说明了基于深度学习方法构建信用评估模型的有效性和可靠性，该研究成果也为探索和丰富符合信用评估管理方法提供了一些借鉴和参考。