基于响应面的三自由度超声电机定子设计优化*

牛子杰， 孙志峻， 崔永杰

(1.西北农林科技大学机械与电子工程学院 西安，712100) (2.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

引 言

随着机器人技术的不断发展，传统的单自由度电机很难满足行业对电机设备的要求，而多自由度(multi-degree of freedom,简称M-DOF)电磁电机制造和控制难度大，成本高，传动装置复杂[1-2]。超声电机是利用压电陶瓷的逆压电效应，将弹性材料的微观形变转变为转子的宏观运动的换能元件。其具有速度快、转矩大、响应快、分辨率高、功率密度高、无电磁干扰[3-4]等特点。因此，超声电机在实际应用中可以替代一些低功率电磁电动机，同时其灵活多变的设计形式可以满足不同工程对M-DOF电机的实际需求，具有广阔的应用前景[5]。

近年来，国内外的专家在M-DOF超声电机设计方面提出了大量的方案，主要分为组合式和多模态式两大类。组合式是多个独立的超声电机定子并联驱动同一个球转子的结构。Masahiko等[6]将M-DOF超声电机应用于内窥镜摄像机镜头转向机构。采用3个行波超声电机定子并联的形式共同驱动球转子转动，旋转位置精度误差在2°以内。Nishizawa等[7]将M-DOF超声电机应用于空间卫星，解决卫星碎片清除问题。通过4个行波超声电机定子并联的形式驱动球转子转动，分别测试了电机的耐久性和寿命，以达到卫星对电机耐久性的要求。Zhang等[8]提出了利用3个直线超声电机并联驱动机械手，实现宏观与微观控制。宏观粗定位误差在2 mm以内，微观精细定位误差在1 μm以内。Wang等[9]研究了3行波环形定子组成的2-DOF超声电机的摩擦特性以及最优控制策略，得到电机的最大空载转速和堵转扭矩分别为92 r/min和90 mN·m。

多模态式M-DOF超声电机主要是依靠定子的多种共振模态叠加和组合实现球转子的M-DOF转动。Yan等[10]采用4个压电陶瓷片和一个带凸缘的金属底座通过粘接组合为一个多自由度定子，利用纵向模式和弯曲模式两种模态的叠加实现驱动足的三自由度运动，实验并测试得到驱动足的输出速度达到327 r/min。Zhang等[11]提出了一种基于3-DOF超声电机的机器人手指关节，电机采用夹心式的振动器，在电压作用下实现纵振和弯振的组合，最终获得最大输出扭矩约23.5 mN·m。Zhou等[12]提出一种新的2自由度平面直线超声电机，电机由两个换能器和两个等腰三角形构成，通过弯曲振动模态和纵向振动模态叠加生成驱动足的椭圆运动，在400 V的激励电压作用下，实现最大推力为3.15 N。Takemura等[13]将3-DOF超声电机应用于微创手术机械手腕关节结构，利用圆柱状定子的3种固有振动模式实现球转子的3-DOF运动，最终设计并加工了手术钳的腕关节。

以笔者在文献[14]中提出的一种基于球面接触副的超声电机驱动的多自由度关节为研究对象，提出了一种基于响应面模型的3-DOF超声电机设计与优化策略。对3-DOF超声电机进行运动学分析建模，通过负载模型分析得到电机最佳驱动频率范围，用响应面法对定子最佳频率对应的模态进行设计和优化，得到满足设计要求的3-DOF超声电机。

1 3-DOF超声电机结构和优化策略

1.1 3-DOF超声电机结构和工作原理

文献[14]中提出的3-DOF超声电机其基本结构如图1所示。该电机包含3个环形定子，3个柔性底座，1个支架和1个球转子。定子背面通过环氧胶粘接固化了环形压电陶瓷片，压电陶瓷片采用环形超声电机B05模态的分区极化[15]。3个定子中心线交于一点，呈120°夹角分布。定子表面有齿状结构，同时齿面形貌是和球转子表面同曲率半径的圆弧，保证球转子和定子能够紧密贴合。每个柔性底座都有弹性结构，保证电机在装配完成后球转子和定子之间具有一定的预紧力。

图1 3-DOF超声电机结构Fig.1 Structure of 3-DOF ultrasonic motor

根据文献[16]考虑电机结构结合系统辨识方法提出了该电机的力学模型。在该模型中引入理想转速ωid，理想转速是定转子之间没有相对滑动时的电机转速，理想转速的表达式如式(1)所示

(1)

其中：k为定子一周中的波长个数；b为定子直径；h为定子的有效厚度。

可以看到通过改变驱动电压的频率可以实现转速的控制。电机实际工作中由于定转子的机械摩擦驱动特性，电机的实际转速ω并不等同于理想转速ωid。通过实验方法，描绘具有相同共振频率，不同理想转速(不同尺寸)的定子装配得到的电机扭矩-转速特性特性曲线。根据曲线可发现横坐标(转速)的截距与电机理想转速相同，曲线斜率与定子共振频率相同。由此可得电机的输出扭矩[16]为

Td=f0(ωid-ω)

(2)

其中：f0为电机的共振频率，可以通过实验结合系统辨识得到。

由式(2)可知设计初期，电机的输出扭矩与电机的共振频率成比例关系，因此要在设计初期引入对电机输出扭矩的设计，就对应于对电机共振频率的设计。在确定的共振频率点附近对电机结构进行优化，就是保证了电机共振频率的值不变，从而保证了电机输出扭矩不变。但是围绕共振频率点附近对定子进行优化，保证定子共振频率值不变则需要解决如下问题：a.定子设计模态与干扰模态分离不彻底；b.定子在相同电压下振动幅度偏小；c.定子内应力较大，超过了材料的许用应力。

1.2 3-DOF超声电机定子设计与优化策略

该电机使用的定子所利用的模态为金属圆环面外正交模态，如图2所示。在定子背面粘接的压电陶瓷通高频电压信号后，压电陶瓷由于逆压电效应产生高频伸缩效应，该高频伸缩效应以激励源的形式诱发定子圆环产生一对正交的振动模态记为B05。这两种模态均在定子表面产生机械驻波，而两相机械驻波的叠加则在定子表面产生了行波。

图2 3-DOF超声电机定子的工作模态Fig.2 3-DOF working mode of the stator

由圆环形定子的工作原理可知，该电机的定子利用两相正交模态叠加的形式产生行波，因此设计优化时首先要考虑有效模态与干扰模态的分离问题；同时电机输出高扭矩和高转速的前提是定子振幅要大；最后定子在振动过程中内应力不能过大，应该小于材料的屈服极限。要同时满足这些设计要求，则需要解决多目标优化的问题。笔者依靠响应面近似模型和试验设计方法来实现3-DOF超声电机定子设计与优化。具体的做法是选取适当的定子结构参数作为设计变量，利用拉丁超立方抽样方法在变量空间选择样本点，针对不同样本点的组合，利用(ANSYS parametric design language，简称APDL)建立有限元模型并对定子进行模态分析和谐响应分析，得到对应各样本点的响应值(包括前相频率和后相频率、定子表面振幅和定子内应力等)，利用样本点和响应值建立定子优化的响应面模型，再以遗传算法进行寻优，具体流程如图3所示。

图3 3-DOF超声电机定子优化设计流程Fig.3 Optimal design flow of 3-DOF ultrasonic motor stator

2 电机定子响应面模型

2.1 数值建模

图4为3-DOF超声电机定子的结构尺寸简图，其涉及到的结构尺寸参数总共13个，其中变化尺寸参数共5个，主要包括：本设计提到的在水平方向和竖直方向影响电机振动特性的主要尺寸,为P3,P7,P8,P10,P12；固定尺寸8个，包括电机定子满足结构需求的基本尺寸,为P1,P2,P4,P5,P9，P11,P13；元器件供应商所决定的尺寸；以及由尺寸链可以换算得到的尺寸。表1为定子变化尺寸及其设计空间。为了获得较大的振幅，定子采用QSn6.5磷青铜材料，弹性模量为92 GPa，密度为8 500 kg/m3，泊松比为0.33；压电陶瓷材料采用PZT-8,密度为7 500 kg/m3, 刚度矩阵cE、压电矩阵e和介电常数矩阵εs分别如式(3)～(5)所示。

图4 3-DOF超声电机定子的结构尺寸简图Fig.4 Structure size diagram of the stator of 3-DOF ultrasonic motor

mm

(3)

(4)

(5)

根据图4和表1所示的定子结构和相关尺寸值，以及定子的固定尺寸值，通过APDL可以建立定子的有限元模型。定子采用8节点6面体的SOLID45单元，压电陶瓷材料采用8节点6面体的SOLID5单元，最终将定子划分为40 640个单元，共计50 120个节点，同时定子为自由边界条件。定子的有限元模型如图5所示。通过模态置信准则(modal assurance criteria，简称MAC)方法。对定子模态进行自动识别时需要选取参考振型[17]，参考振型选取的参考节点为定子齿面最外圈的节点，如图5所示。图6为初始尺寸模态计算得到的定子两相模态对应的两个机械波长参考节点振动特征。

图5 定子有限元模型Fig.5 Structure size diagram

图6 参考节点振动特征Fig.6 Vibration characteristics of reference nodes

2.2 优化目标函数确定

关于3-DOF超声电机定子的优化涉及到多方面的要求，这些设计要求必须在优化算法的目标函数中得到体现。每个目标函数是对实际设计要求的数学描述，反映定子的某个(或某些)特性。根据结构及振型调整的要求及超声电机设计的一般准则，定子部分所涉及的所有设计要求(优化目标)可以概括为4个目标函数。

1) 前相干扰模态频率远离工作模态频率。比定子工作模态频率低的频率有很多，如果这些频率与工作模态频率相近，会导致定子产生不需要的振动位移，从而使得电机输出性能下降。为了保证电机的性能，要求电机的工作模态频率尽可能大于这些干扰频率，差值越大越好。同时为了数据处理方便和目标函数的收敛特性，采用两者差值的倒数作为优化函数，如式(6)所示

(6)

其中：FAB为定子工作模态对应的共振频率；FF为前相共振模态对应的共振频率。

2) 后相干扰模态频率远离工作模态频率。与前相干扰模态一样，后相干扰频率也很多，如果这些频率与工作模态频率相近，会导致定子产生不需要的振动位移，使得电机输出性能下降。为了保证电机的性能，要求电机的工作模态频率尽可能小于这些干扰频率，差值越大越好。优化函数为

(7)

其中：FL为后相共振模态对应的共振频率。

3) 定子齿面振幅。超声电机运动的原理决定了定子齿面振幅对电机性能的影响很大。振幅在一定范围内越大性能越好。因此定子齿面质点在设计模态下沿着振动方向的振幅值也作为一个目标函数。考虑到函数归一化处理和收敛性要求，取定子齿面振幅的倒数作为目标函数，如式(8)所示

(8)

其中：ZA为A相激励时定子齿面的振幅；ZB为A相激励时定子齿面的振幅。

4) 定子安装部位内应力。超声电机运动主要依靠定子的振动将压电陶瓷的变形放大。对于定子最内圈的安装部位应该保证变形越小越好，即该部位内应力越小越好。因此安装部位的内应力作为目标函数如式(9)所示

F4=σ

(9)

其中：σ为定子安装部位的内应力。

由以上分析可知，3-DOF超声电机定子的优化为多目标优化设计，直接针对多个目标函数进行优化很难得到好的最优结果。为了便于寻找最优解，本研究采用“统一目标函数”法。首先，将各目标函数都转化为无量纲的值，并将其限定在[0,1]范围内，即根据各个目标函数的权重，给各目标函数加权因子；然后将各目标函数与各自加权因子的乘积求和作为最终的目标函数。具体如式(10)所示。

(10)

其中:βi为各目标函数的加权系数；Fi为各子目标函数。

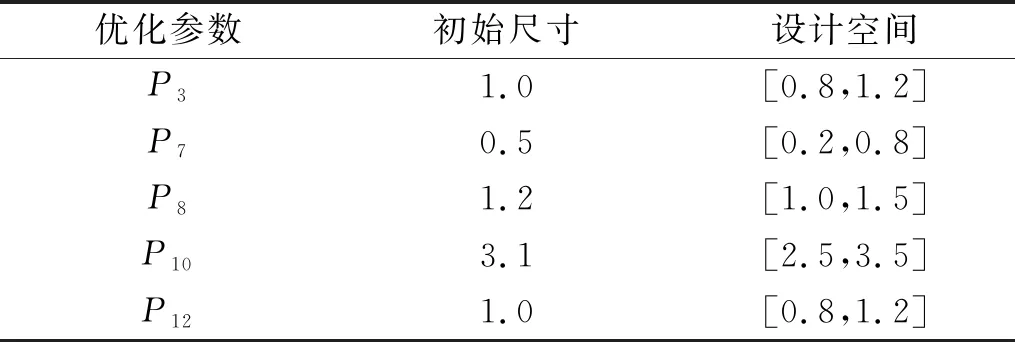
本实验中加权系数共取βa,βb,βc,βd4组，如式(11)所示。

(11)

2.3 优化子目标响应面函数的确定

表1中的P3,P7,P8,P10,P12为可变参数，选择5个尺寸作为设计变量，则实验设计变量如式(12)所示。

(12)

同时采用拉丁超立方抽样实验设计方法，进行5因素设计。本研究所取得变化尺寸均是直接影响到定子振动特性的尺寸。在选取变化尺寸的时候主要考虑半径方向，厚度方向相互独立的尺寸，即一个尺寸的改变不会影响其他尺寸的变化，从而保证了变量间的独立性，为拉丁超立方抽样提供了条件。由表1可得初始值为[1.0,1.5,1.2,3.1,1.0]，同时可得各设计变量的取值范围如式(13)所示。

(13)

通过多学科优化设计软件Optimus，对各子目标函数进行拉丁超立方抽样实验设计[18]，得到56组数据，表2所示的为其中的20组数据。其中，x1～x5分别对应可变尺寸P3,P7,P8,P10,P12，为了获得高质量的响应面模型，笔者采用二阶泰勒级数展开可获得如下子目标函数模型。

表2 拉丁超立方抽样实验样本

Tab.2 Experimental sample of Latin hypercube sampling

序号P3P7P8P10P12F1(x)F2(x)F3(x)F4(x)x1/mmx2/mmx3/mmx4/mmx5/mm1/Hz1/Hz1/μmPa10.871 20.423 11.158 93.235 90.980 81.64×10-42.10×10-45.73×1052.34×10621.120 90.619 51.269 92.532 20.918 51.10×10-32.45×10-46.32×1053.68×10630.846 00.313 21.105 63.283 40.866 22.80×10-42.48×10-45.47×1052.17×10641.175 80.487 91.192 12.675 30.835 85.66×10-42.78×10-45.51×1053.97×10650.938 30.344 01.059 13.203 31.174 22.89×10-42.75×10-45.52×1052.07×10660.878 80.404 71.098 43.356 00.877 71.55×10-42.68×10-45.58×1052.30×10671.083 70.727 11.386 52.506 90.815 82.01×10-32.48×10-41.11×1062.44×10680.846 40.766 41.108 92.521 30.815 06.38×10-42.48×10-46.77×1053.70×10690.905 20.438 81.112 53.148 50.927 31.54×10-42.24×10-45.64×1052.29×106

1) 子目标函数F1的响应面模型如式(14)所示，其中a0～a20分别为各项的系数。

(14)

由表2数据结合Optimus可得a0～a20的值分别见表3所示。同时得到决定系数R2=86%。

表3 子目标函数F1的系数

Tab.3 The coefficient of the objective function F1

a0～a6取值a7～a13取值a14～a20取值a0-6.8×10-3a74.0×10-3a14-4.5×10-3a1-5.3×10-6a82.3×10-3a15-4.9×10-2a2-9.6×10-3a9-1.4×10-2a16-7.8×10-3a3-1.8×10-2a101.0×10-2a17-6.3×10-3a4-3.5×10-3a112.4×10-2a187.9×10-3a5-6.9×10-3a123.4×10-3a194.2×10-3a6-1.9×10-2a13-2.3×10-2a205.1×10-3

2) 子目标函数F2的响应面模型如式(15)所示，其中b0～b20分别为各项的系数。

(15)

可得b0～b20的值分别见表4所示。同时得到决定系数R2=86%。

表4 子目标函数F2的系数

Tab.4 The coefficient of the objective function F2

b0～b6取值b7～b13取值b14～b20取值b0-7.4×10-3b74.3×10-3b14-1.4×10-3b14.3×10-3b82.3×10-3b15-5.7×10-2b2-1.5×10-2b9-1.5×10-2b16-8.1×10-3b3-2.0×10-2b101.2×10-2b17-9.5×10-3b4-2.1×10-3b112.7×10-2b181.1×10-2b5-5.9×10-3b125.9×10-3b196.6×10-3b6-2.2×10-2b13-2.5×10-2b206.4×10-3

3) 子目标函数F3的响应面模型如式(16)所示，其中c0～c20分别为各项的系数。

(16)

可得c0～c20的值分别见表5所示。同时得到决定系数R2=88%。

表5 子目标函数F3的系数

Tab.5 The coefficient of the objective function F3

c0～c6取值c7～c13取值c14～c20取值c0-6.6×105c75.9×105c14-9.4×105c1-4.6×104c84.7×105c15-8.7×106c2-1.7×106c9-2.5×106c16-1.6×106c3-3.2×106c101.9×106c17-1.1×106c4-5.6×105c114.1×106c181.5×106c5-1.3×106c126.9×105c196.8×105c6-3.5×106c13-4.1×106c208.3×105

4) 子目标函数F4的响应面模型如式(17)所示，其中d0～d20分别为各项的系数。

(17)

可得d0～d20的值分别见表6所示。同时得到决定系数R2=88%。

表6 子目标函数F4的系数

Tab.6 The coefficient of the objective function F4

d0～d6取值d7～d13取值d14～d20取值d02.8×106d7-3.7×105d147.6×105d16.7×105d8-2.1×105d151.5×106d2-1.2×105d91.3×106d167.4×105d36.1×105d10-2.4×105d171.2×105d4-1.7×105d11-5.0×105d186.9×104d54.8×105d124.8×105d194.0×105d67.5×105d139.2×105d204.8×105

2.4 响应面函数分析

根据子目标函数响应面表达式(14)～(17)及子目标函数系数表3～6的分析可以得到如下结论：影响子目标函数F1的主要优化变量为P3和P8；影响子目标函数F2的主要优化变量为P7和P8；影响子目标函数F3的主要优化变量为P7和P8；影响子目标函数F4的主要优化变量同样为P7和P8。

3 电机定子优化设计

3.1 自适应遗传算法

由于本研究涉及到的优化参数较多，优化目标函数的基函数项也比较多，因此文中采用自适应遗传算法进行优化。自适应遗传算法是一种简化的模拟生物遗传和变异过程的算法。本研究用到的自适应遗传算法是一种基于真实值的连续参数优化算法[18-19]，结合本研究的实际工程情况，自适应遗传算法主要参数设置为：父代数为20，种群大小为50，步长突变因子为1.3，停止准则为1×10-5。

3.2 数据分析

根据式(12)提供的4种加权系数的组合，结合自适应遗传算法，建立各子目标函数与最终的目标函数之间的关系；依靠响应面模型对最终的目标函数Fo bj进行优化。优化结果如表7所示，其中*为最优结果组。

对比表7中的4种加权系数组合得到的优化结果，可以得到第3组的优化结果为最优。其中总体优化目标函数Fo bj在4个组合中趋于最小值0.048 8。F1，F3和F43个子优化目标的收敛值也是4个组合中的最小值。子优化目标F2的收敛值在4个组合中并非最小值原因在于：根据式(14～17)得到四个子优化目标的主要影响尺寸变量为P7和P8，同时根据图6可以看出这两个尺寸在一个方向上，属于耦合尺寸，因此想要寻求最优解只能在两个尺寸之间找到一个平衡点，保证多数优化目标最优的同时少数或者单个优化目标满足基本要求。

该组总体优化目标函数Fo bj和4个子优化目标函数F1～F4的收敛情况分别如图7的(a～e)所示。经过了85次迭代，总体优化目标和4个子优化目标都收敛于固定值。

表7 不同加权系数对应的优化结果

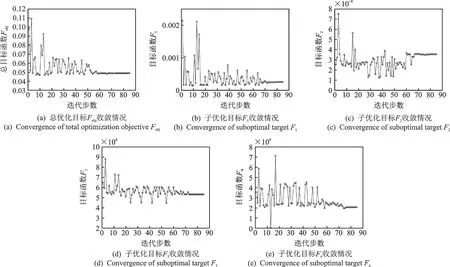
图7 目标函数收敛情况Fig.7 Convergence of objective function

3.3 数据验证

为了验证表7中优化结果的正确性，本研究利用ANSYS软件对各组优化后的尺寸进行了有限元计算，同时将优化目标进行反规格化处理。将有限元计算的结果与响应面模型优化的结果进行对比分析(如表8所示)验证了响应面模型优化的正确性。

由表8可以看出第3组优化结果：前相干扰频率与工作模态频率之间的差值响应面优化结果为3 952 Hz，有限元计算得到的前相干扰频率与工作模态频率之间的差值为4 018 Hz；后相干扰频率与工作模态频率之间的差值响应面结果为2 824 Hz，有限元计算得到的前相干扰频率与工作模态频率之间的差值为2 787 Hz；振动幅值响应面优化结果为1.88 μm，有限元计算的结果为1.92 μm；内应力响应面优化结果为2.05×106Pa，有限元计算的结果为2.33×106Pa。计算结果表明前相干扰频率差值，后相干扰频率差值，振动幅值和内应力及实际计算一致性较好，同时均满足要求，可见采用的统一目标函数法基本可实现多目标优化设计的需求。根据表7第3组加权系数组合得到的优化结果，将尺寸参数圆整到精度为0.01 mm，利用ANSYS软件重新计算，并与定子初始值计算得到的结果进行比较，结果如表9所示。

表8 定子优化结果反规格化数据与ANSYS计算结果对比验证

Tab.8 Comparison of inverse optimization data and ANSYS calculation results of stator optimization results

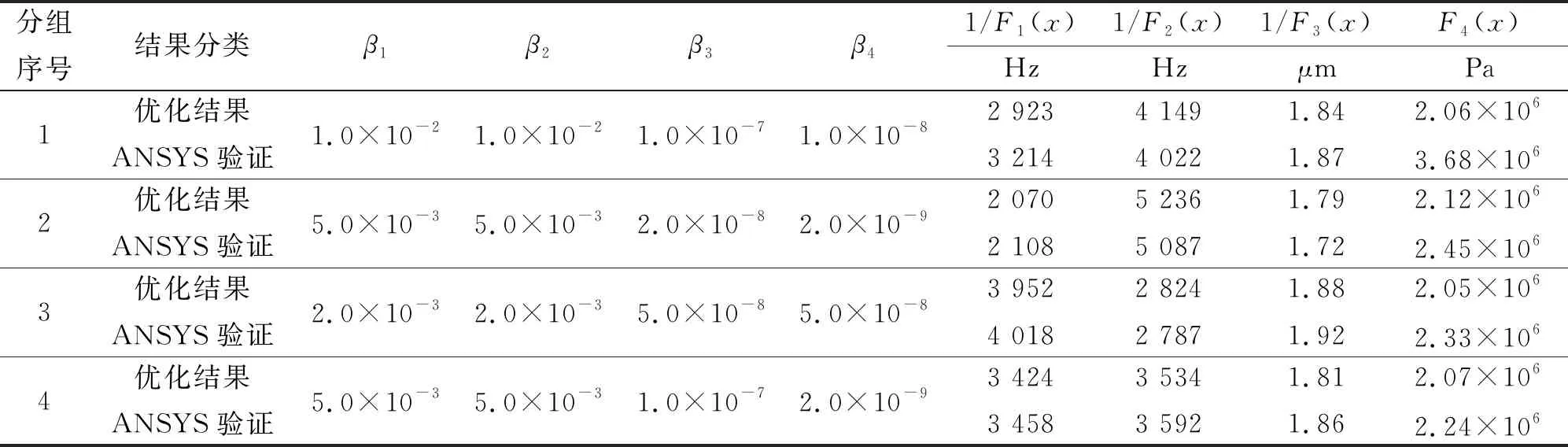
分组序号结果分类β1β2β3β41/F1(x)1/F2(x)1/F3(x)F4(x)HzHzμmPa1优化结果ANSYS验证1.0×10-21.0×10-21.0×10-71.0×10-82 9233 2144 1494 0221.841.872.06×1063.68×1062优化结果ANSYS验证5.0×10-35.0×10-32.0×10-82.0×10-92 0702 1085 2365 0871.791.722.12×1062.45×1063优化结果ANSYS验证2.0×10-32.0×10-35.0×10-85.0×10-83 9524 0182 8242 7871.881.922.05×1062.33×1064优化结果ANSYS验证5.0×10-35.0×10-31.0×10-72.0×10-93 4243 4583 5343 5921.811.862.07×1062.24×106

表9 初始值与终止值对照

Tab.9 Comparison between initial value and

termination value

优化相关变量优化前优化后优化参数P3/mm1.000.95P7/mm0.500.35P8/mm1.201.02P10/mm3.103.37P12/mm1.000.90优化目标1/F1(x)/Hz1 0254 0181/F2(x)/Hz1 5322 7871/F3(x)/μm0.971.92F4(x)/MPa5.982.33目标频率/kHz23.6722.88前相干扰频率/kHz22.6418.87后相干扰频率/kHz25.2925.67

3.4 实验验证

本实验采用PSV多普勒激光干涉仪对根据优化前后尺寸加工得到的定子进行扫描和测振。主要测量得到定子的共振频率和共振频率下定子的振幅，实验过程中定子的激励峰值电压为100 V。由实验可得定子的振动模态如图8所示，同时实验得到定子振幅如表10所示。

由图8可得测试得到的定子振动模态与计算保持一致。根据表10的实验结果分析可得：优化后的定子z方向的振幅明显增大，证明了本研究提出的定子优化方案的有效性。

图8 实验得到的定子振动模态Fig.8 Vibration mode of the stator obtained from the test

优化A相B相FA/kHzzA/μmFB/kHzzB/μm优化前23.380.8523.540.90优化后22.861.9522.852.00

4 结束语

针对3-DOF超声电机定子的多目标优化问题，笔者提出一种基于响应面模型的多目标优化方法，对定子前相干扰频率、后相干扰频率、齿面振幅和内应力进行了多目标优化。优化结果表明，优化后的定子前相干扰频率与目标频率之间的差值大于3 500 Hz，定子后相频率与目标频率的差值大于2 500 Hz，定子齿面振幅大于1.9 μm，定子内应力小于2.5 MPa，均满足定子设计的基本要求。同时该方法使得普通的有限元计算中手动选择参数变为自动计算获得最优解，为更复杂的多目标优化设计提供了思路，大大缩短了优化设计的周期。