基于LHS冷却塔敏感性分析及频率估算*
柯世堂, 徐 璐,2
(1.南京航空航天大学土木工程系 南京,210016) (2.中国能源建设集团广东省电力设计研究院有限公司 广州,510700)
引 言
自振频率是决定着结构动态变形和受力的关键因素,现有冷却塔结构自振频率主要通过有限元计算或现场实测来获取,计算过程复杂、耗时长且方法单一,缺乏简单有效的冷却塔自振频率估算公式。而现阶段国内外研究成果[1-3]和规范[4-6]中鲜有给出简单快捷的冷却塔自振频率估算公式;此外,冷却塔基频对何种结构参数较为敏感也尚未得出一致结论。文献[7-8]给出了多参数下自振频率的拟合公式,然而并未对其结构参数进行敏感性分析。因此探究不同参数下动力特性的敏感性,通过附加敏感因子权重值拟合出自振频率的估算公式,并进行精细化验证具有重要的理论和工程意义。
针对结构动力特性的敏感性分析,主要集中在大跨度桥梁和屋盖,文献[9-10]提出了基于高斯过程模型的全局灵敏度分析方法,分析了实桥动力特性不确定性的灵敏度。文献[11]针对某大跨屋盖采用扰动法和拉丁超立方抽样法进行多参数下结构自振频率的敏感性分析。文献[12-13]采用扰动法进行了刚性悬索加劲钢桁梁桥结构参数敏感性分析和矢跨比等参数对辐射式张弦梁结构地震响应的敏感度分析。此外,针对大型冷却塔动力特性的研究,文献[14]基于现场实测数据对冷却塔动力特性进行分析。文献[15]发现冷却塔低阶频率主要受环向刚度控制,子午线型与结构整体抗倾覆弯矩有关。文献[16]通过建立与渡桥电厂冷却塔相同壁厚、高度、筒底直径和人字柱等参数的冷却塔,分析两者动力特性和风致响应的差异,结果表明塔型不合理是渡桥电厂冷却塔倒塌的重要原因之一。文献[8,17]对3种不同特征尺寸的冷却塔进行了动力特性分析,研究发现基频较低的冷却塔共振响应占据主导地位,随基频的降低风振响应的动力放大作用愈加显著。已有研究均未涉及参数的敏感性分析,这也成为设计人员在进行塔型优化过程中的瓶颈问题。
鉴于此,以国内某179 m高的大型冷却塔为基准塔,首先,通过改变模型典型结构参数获得基准塔38个模型的动力特性,提炼出基频和倾覆频率随结构参数的变化规律;然后,采用扰动法和拉丁超立方抽样两种方法进行结构自振频率参数的敏感性分析,获取了不同阶数下各结构参数的敏感因子,在此基础上首次拟合出考虑敏感因子权重值的多参数基频和倾覆频率的实用估算公式;最后,选取课题组已有研究的冷却塔进行估算公式的误差分析,进而验证了笔者提出的自振频率估算公式精度高、稳定性好。
1 基准塔有限元建模及动力特性分析
1.1 有限元建模
基准塔塔高为179 m,喉部直径为98.6 m,进风口高度为27.8 m。采用大型通用软件ANSYS建立基准塔模型,图1给出了冷却塔的主要构件:刚性环、塔筒、支柱和地基。塔筒采用Shell63单元,环向和子午向分别划分192和118个单元。环基及与环基连接的48对X型柱均采用Beam188单元。

图1 冷却塔有限元建模示意图Fig.1 Sketch map of finite element modeling of cooling tower
X型支柱与塔筒下部连接采用节点自由度耦合的方式,每个环基下部采用Combin14单元,每根桩基均采用3个力弹簧单元和3个力矩弹簧单元分别模拟桩沿竖向、环向、径向、绕竖向、绕环向和绕径向的作用,弹簧单元一端与环基刚性连接,另一端固结约束。
1.2 自振特性分析
采用Block Lanczos方法求解基准塔的自振频率和振型,图2和表1分别为冷却塔前10阶自振频率分布曲线和典型振型列表。该基准塔的基频为0.678 Hz,前10阶频率均小于1.0 Hz。结构振型复杂且具有明显的三维特征,具体表现为:子午向均存在至少2个谐波,随阶数增加底部谐波所处高度逐渐降低,且环向谐波数随阶数增加而增大。
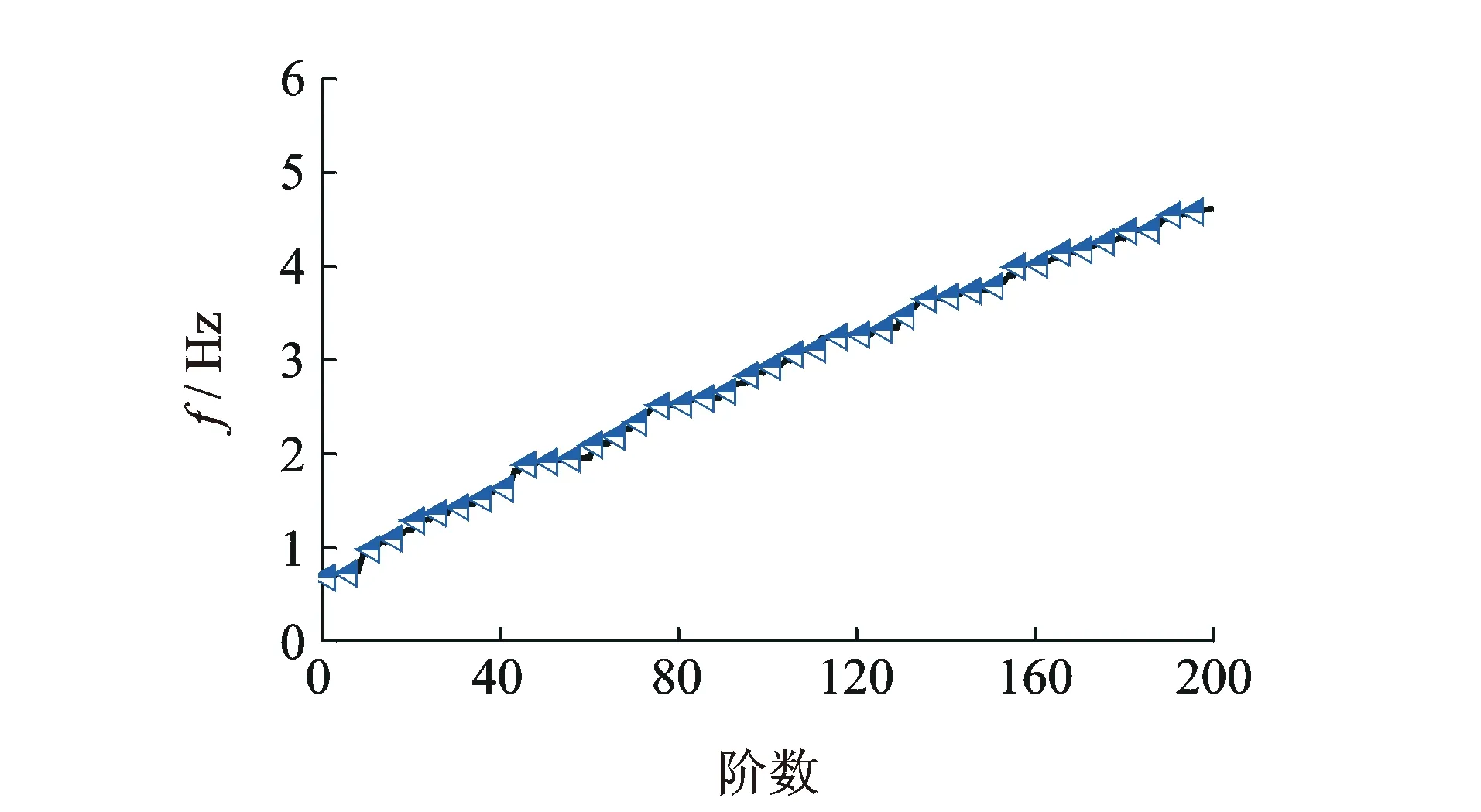
图2 冷却塔自振频率分布示意图Fig.2 Distribution of natural frequency of cooling tower
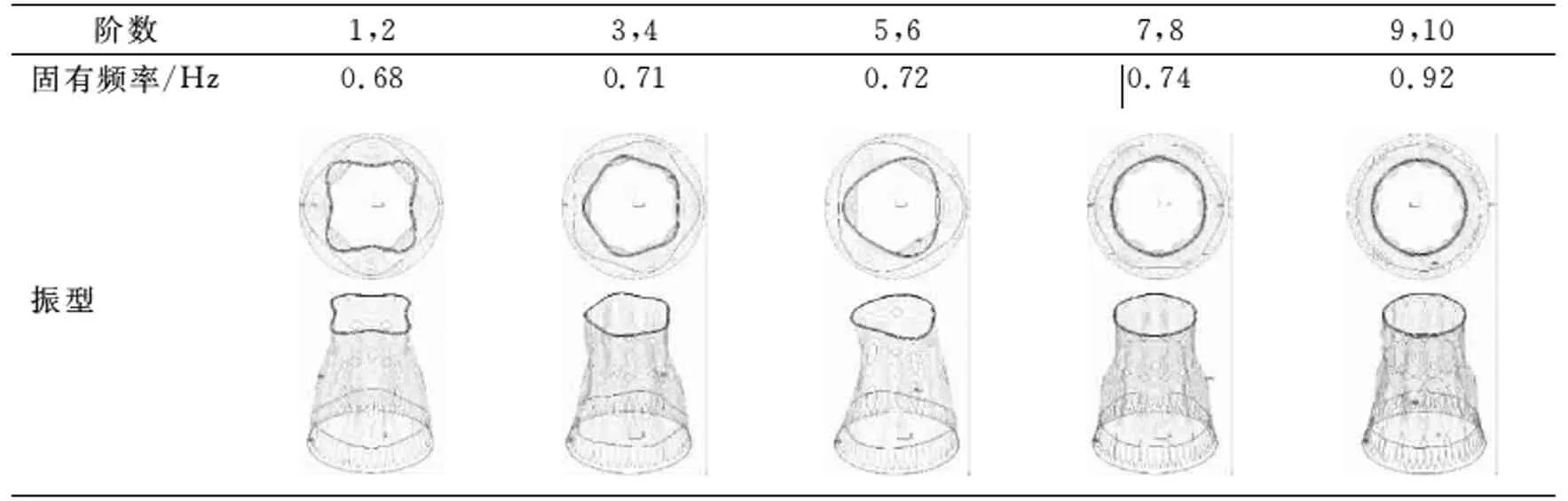
表1 冷却塔前10阶固有频率和振型列表
2 自振频率的参数分析
冷却塔作为双曲薄壳结构,主要结构设计参数包括塔度、喉部直径、进风口位置、支柱截面积和地基刚度。建模过程中一般采用弹簧单元模拟真实结构与土之间的相互作用,研究[18-19]表明,弹簧刚度对结构基频存在影响,在一定范围内随刚度增加自振频率增大,当增至一定限度后自振频率出现减小的趋势。冷却塔地基弹簧刚度一般采用经验公式[15,20]计算
(1)
其中:D为地基周长;Li(i=1,2,3)分别为地基弹簧沿竖向、径向和环向长度;K为基床系数;Ni(i=1,2,3)为绕竖向、绕环向和绕径向单元个数。
由式(1)可知,弹簧刚度由多参数决定,其中包括基床系数(主要与结构所处土质有关)、有限元建模时基础单元数量、地基周长和地基的尺度等参数。经验公式中弹簧刚度计算的参数存在较多不确定性,如基础单元的数量,因此在变量设置后得出的估算公式将与实际存在较大偏差。本研究未考虑弹簧刚度对冷却塔频率的影响,而将其他关键参数均考虑在内,文献[15-16,20]针对少部分结构参数进行探讨,但未针对以上全部关键参数进行研究,更未涉及结构参数的敏感性分析。
为研究塔高、喉部高度、喉部直径、进风口高度和支柱截面对冷却塔自振特性的敏感性,以基准塔为例,在保持其他参数不变并控制单一变量的前提下,对各个模型进行动力特性分析,具体参数分析如表2所示。
图3和4给出了不同高度、喉高比、喉部直径、进风口高度和支柱截面积下冷却塔的基频和倾覆频率结果,在此基础上拟合出基频随各参数变化的分布曲线。由图可知:a.基频随冷却塔高度增加逐渐减小,最大减幅为55%,说明塔高与自振频率呈负相关关系且相关性较强;倾覆频率也随塔高的增加逐渐减小;b.随喉高比的增大结构基频大致呈下降趋势,喉高比与结构自振频率呈负相关关系,在0.76~0.79范围内出现了平缓区;倾覆频率随喉高

表2 结构参数列表
比的增大呈先增后趋于平缓再减的趋势,在0.76~0.79范围内出现了平缓区;c.随喉部直径的增大基频逐渐增大,喉部直径与结构自振频率呈正相关关系,但结构倾覆频率随喉部直径的增大逐渐减小;d.进风口高度的增加使得结构基频呈非线性增加的趋势,最大增幅仅为6%,进风口高度与基频呈正相关关系;此外,倾覆频率随进风口高度的增加逐渐减小,但最大减幅仅在2%左右;e.支柱截面积与结构自振频率呈对数律分布,当截面积增大至一定数值(2 m2),结构基频增长趋势变缓,最大增幅为9.8%,与塔高相比,自振频率与支柱截面积相关性较弱。

图3 冷却塔各参数与基频的关系曲线Fig.3 The relative curve between each parameter of cooling tower and the natural frequency of vibration

图4 冷却塔各参数与倾覆频率的关系曲线Fig.4 The relative curve between each parameter of cooling tower and the natural frequency of vibration
3 自振频率参数的敏感性分析
3.1 扰动法

(2)
其中:ffem为求解函数;H为塔高;B为喉高比;R为喉部直径;J为进风口高度;A为支柱截面积。
扰动法计算各模态灵敏度的公式为
(3)
其中:λj为p=p0时的自振频率;λj′为保持其他参数不变,令p=p0+Δp时算出的自振频率;p为各种设计参数。
通过式(3)求得的灵敏度无量纲化如下
(4)
无量纲化的灵敏度称为相对灵敏度。本研究将其作为衡量各参数敏感度的指标,分析5种设计参数对冷却塔自振频率的敏感度,分别用|H|,|J|,|R|,|B|和|A|来表示。
冷却塔结构具有轴对称性,其奇数和偶数阶频率一致,因此图5以奇数阶为例给出了5种设计参数对前10阶自振频率的相对灵敏度柱状图。分析表明:a.塔高和喉部高度对模型自振频率的敏感因子均为负值,表明其与结构的自振频率呈负相关关系;喉部直径、进风口高度和支柱截面积的敏感因子为正值,表明其与自振频率呈正相关关系;b.冷却塔高度对结构自振频率的敏感度较大,敏感因子均在-1.5~-2.0之间,喉部高度、喉部直径和支柱截面积的敏感因子均较小,在±0.0上下波动,而对于进风口高度,在低阶敏感因子较小,高阶敏感因子增大,最大可至0.5左右;c.各设计参数对结构自振频率的敏感度按从小到大的排列顺序|H|>|J|>|B|>|A|>|R|。

图5 各设计参数的相对灵敏度曲线图Fig.5 Relative sensitivity curve of design parameters
3.2 拉丁超立方抽样法


图6 各参数变量的等概率区间划分Fig.6 Equal probability interval division for parametric variables
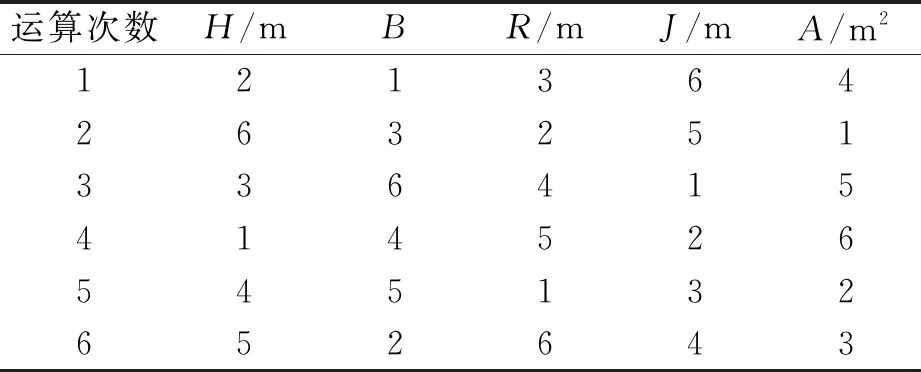
运算次数H/mBR/mJ/mA/m2121364263251336415414526545132652643
自振频率的计算参数x1,x2,…及频率的相关矩阵为
(5)
其中:C为各计算参数x1,x2…及因变量f的相关矩阵;rij为简单相关系数。
对式(3)求逆矩阵得
(6)
则偏相关系数为
(7)
图7为拉丁超立方抽样方法求得的各种设计参数的敏感因子。对比可知:采用LHS法得出的设计参数敏感度排列顺序如下:a.塔高和喉部高度与结构自振频率呈负相关关系;喉部直径、进风口高度和支柱截面积与自振频率呈正相关关系;b.冷却塔高度对结构自振频率的敏感度较大,敏感因子均在-1.5~-2.0之间,喉部高度、喉部直径和支柱截面积的敏感因子均较小,在±0.0上下波动;c.各设计参数对结构自振频率的敏感度按从小到大的排列顺序|H|>|B|>|A|>|R|>|J|。

图7 各设计参数的相对灵敏度曲线图Fig.7 Relative sensitivity curve of design parameters
3.3 自振频率的实用估算公式
以上分析表明:基频和倾覆频率与塔高呈反比,与支柱截面积呈对数律形式增长,而与喉高比和进风口高度呈非线性关系。基于多项式拟合原理,以塔高、喉高比、喉部直径、进风口高度和支柱截面积为目标函数,笔者拟合给出超大型冷却塔基频和倾覆频率实用估算方式。其中,基频拟合公式为
(8)
倾覆频率拟合公式为
(9)


3.4 误差分析
为验证拟合公式的有效性,采用课题组已有研究的冷却塔进行验证。文献[14,23]中冷却塔结构基本参数如表4所示。
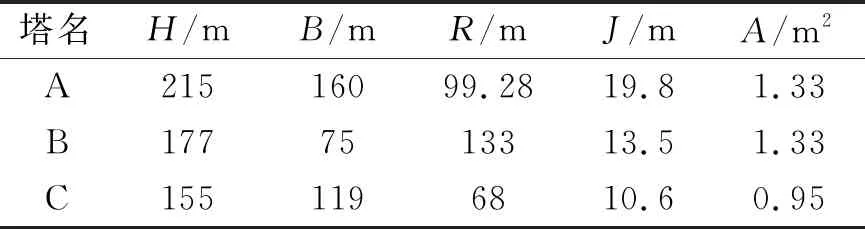
表4 试验塔结构基本参数
表5为3个算例塔基频和倾覆频率有限元计算值和拟合值。对比发现:基频拟合结果误差值大于倾覆频率的误差,其中塔B基频误差最大,为1.95%,塔A倾覆频率误差最小,为0.33%。可见文中的基频和倾覆频率拟合公式在估算自振频率方面具有较高的可信度。
表5 冷却塔自振频率结果验证
Tab.5 The result verification of natural frequency for cooling tower

Hz
4 结 论
1) 冷却塔基频随总高度和喉部高度的增加逐渐减小,而随喉部直径、进风口高度和支柱截面积的增加逐渐增大;以塔高为目标计算所得的敏感因子显著大于其他4个参数的敏感因子,精度较高的拉丁超立方抽样法获取的敏感因子大小排序为|H|>|B|>|A|>|R|>|J|。
2) 冷却塔自振频率与塔高呈线性反比关系,与支柱截面积呈对数律形式增长,而与喉部高度、喉部直径和进风口高度呈非线性关系。基于多项式拟合原理,创新性地提出考虑敏感因子权重值的多参数基频和倾覆频率的实用估算公式。
3) 3个算例冷却塔基频拟合结果误差值大于倾覆频率的误差,其中,塔B基频误差最大,为1.95%,塔A倾覆频率误差最小,为0.33%。可见文中的基频和倾覆频率拟合公式在估算自振频率方面具有较高的可信度。

