考虑支管平面外偏心受力K形加劲相贯节点承载力试验及计算理论

崔鸣诚， 张大长， 刘 鹏， 韩幸宁， 刘 森

(南京工业大学 土木工程学院， 江苏 南京 211816)

近年来，钢管结构因其独特的优越性在国内外得到了较快的发展。K形相贯节点作为钢管结构中一种常用的连接节点，具有传力直接、受力性能好、加工简便、用钢量小、经济指标优越等独特的优点。实际工程中，往往需要对节点部分进行局部加强，以提高节点的承载力和钢材使用率。

然而，由于材质、加工缺陷以及安装所引起的误差，并不能保证节点荷载始终作用在支管轴心处，而支管在平面外方向约束一般较弱，因此压支管平面外偏心受力对节点承载力特性的影响成为研究人员较为关注的问题。

1 研究现状

1.1 相贯钢管节点

国内外规范[1～3]中，无加劲钢管相贯节点的承载力计算方法已较为成熟，但对于外加劲相贯节点承载力的计算方法还比较欠缺。

国内外学者对K形相贯节点的承载力特性做了大量的研究工作[4～6]，Packers等[7]于1982年给出了K形相贯节点最主要的七种破坏模式，并指出其中最为常见的模式为主管表面塑性破坏。陈继祖等[8]在分析各国规范承载力公式的基础上，考虑我国新规范设计原则、材质以及焊接条件，提出了建议的设计承载力公式。陈以一等[9,10]建立了相贯节点极限承载力分析的三重屈服线模型，并建议以主管管壁塑性变形达到0.2%作为节点的极限变形。刘建平等[11]应用材料和几何非线性对T ，Y ，K形圆管相贯节点进行了有限元分析，获得了影响管节点承载力的主要参数与承载力曲线，将有限元计算结果与各国规范进行比较，指出了现有规范的不足之处，为我国规范的进一步修订提供了理论依据。

对于K形加劲相贯节点，张巧珍等[12]应用有限元法，分析计算了无加劲及加劲K形圆钢管相贯节点的承载力，K形和DK形节点承载力随主支管夹角、两支管间隙的变化规律，以及不同几何参数的节间肋板对节点的极限承载力的贡献。李茂华等[13]开展节点承载力对比试验，解释了外加劲环对节点的承载力可以提高30%以上；宋启明[14,15]等开展了不同几何参数对节点承载力影响的试验研究；王晓建等[16]则结合多个试件及有限元计算结果，得到了加劲K形希望管节点的承载力简化计算方法。然而，上述研究均缺少平面外偏心对节点承载力的影响的有关内容。

1.2 平面外偏心受力

国内外有关规范文献中，研究重点主要放在相贯节点的平面外抗弯刚度的分析[17,18]，但关于支管平面外偏心受力对节点承载力特性的影响的研究尚未见报道。而根据有关文献和行业标准[19,20]，根据实际工程经验，由加工缺陷及安装误差导致的结构钢管截面偏心率一般不超过1%。

根据目前研究现状，本文开展了支管平面外偏心荷载条件下K形加劲相贯节点试验及模拟分析，考察其承载力特性及应力分布规律，并重点探讨了支管偏心受力对节点承载力特性的影响。

2 偏心K形相贯节点承载力试验

2.1 试验概况

2.1.1 节点设计

试验共设计2组规格尺寸完全相同的K形相贯节点，其中K1为无偏心节点，K2为偏心受力节点，压支管面外偏心距为0.01D(D为节点主管直径)，主管材质为Q420钢，支管及节点板材质均为Q345钢，焊条为E50焊条。试件规格参数及试验加载条件如表1(表中Fy为主管的屈服承载力)及图1所示。

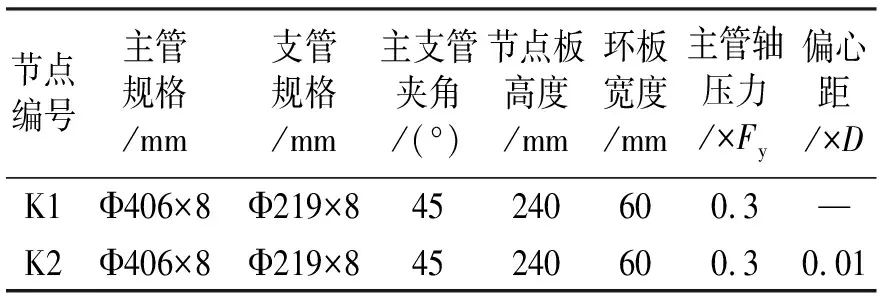
表1 试验节点参数

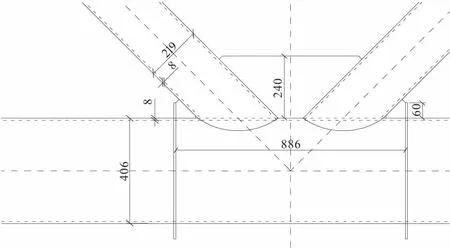
图1 试件规格/mm

2.1.2 加载方法

试验加载装置如图2所示。主管一端靠墙，另一端由5000 kN的液压千斤顶施加主管轴力，支管的拉压力由一对2500 kN穿心千斤顶并联加载。为了预警和防止荷载平面内偏心，压支管两侧设置了侧向的限位装置。同时，在无偏心节点K1的压支管上方布置一道箱型梁，以限制节点在试验过程中在平面外方向的变形，确保支管始终轴心受力，并与未施加压支管面外约束的偏心受力节点K2形成对比。

图2 试验加载装置

试验前，先对液压千斤顶进行标定，并进行对中调整，以保证试验荷载作用在节点主支管轴心处。每次试验前，先预加荷载以消除构件间隙、支座滑移等因素所引起的误差，让节点进入正常工作状态。

加载前，预先利用有限元软件ANSYS对试验节点进行仿真分析，通过模拟荷载位移曲线，利用陈以一等[10]的方法，得到节点的设计承载力。采用力控制方法控制加载速度，等比例同步加载节点主支管，步长随荷载增大而逐渐递减，当支管荷载达到节点的设计承载力，主管荷载恰好达到试验工况确定的主管轴压力，随后保持主管荷载不变，继续加载支管，直至试件发生破坏或无法施加荷载为止。

2.1.3 测试方法

在试验节点的主应力区及节点区粘贴应变片和应变花，测定试验中节点在拉压荷载作用下的应变分布及发展情况，应变片位置及方向如表2及图3所示，每个测点编号对应2个测点，按主管两侧对称布置。

在节点的拉、压支管加载端沿支管轴向分别布置2个位移计，测定加载过程中拉、压支管的轴向变形情况。在平面外偏心受力节点的压支管端板上侧布置两个位移计，以测定加载过程中压支管在平面外方向的位移发展。试验加载过程中，采集系统会自动记录各级荷载下节点各典型位置的应变和支管位移。

表2 应变测点布置

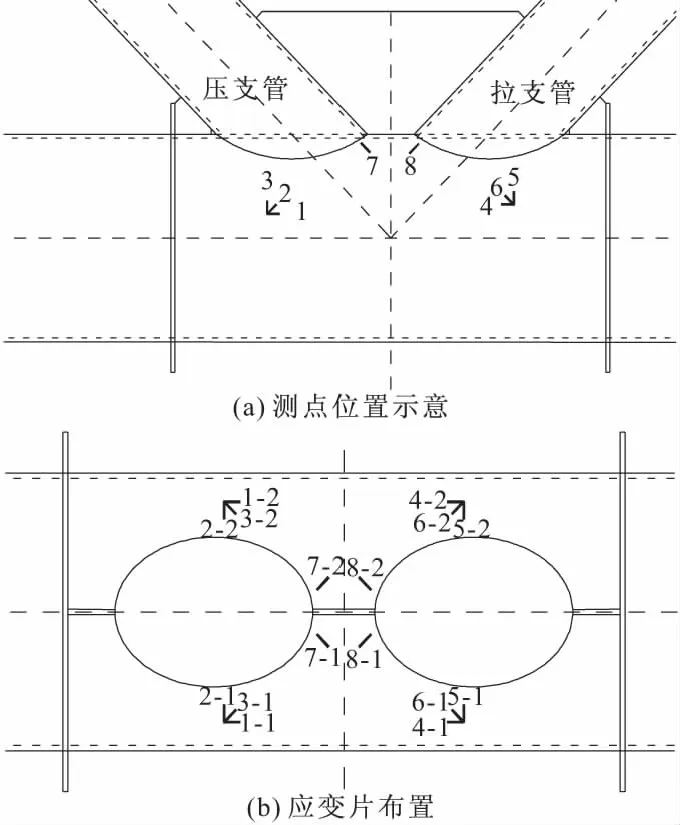
图3 应变测点布置

2.2 试验结果

2.2.1 破坏形式

试验中，无偏心K形加劲相贯节点试件在支管拉压荷载下主要发生主管截面塑性破坏，当支管轴向荷载达到节点极限承载力的95%时，主管与受压支管相贯区域出现明显凹陷，同时侧壁出现外鼓，主管与受拉支管相贯区域开始出现拉凸；继续增大荷载，节点凹凸变形急剧增大，直至达到节点极限承载力，节点破坏。极限状态下，节点板向压支管一侧发生转动，支管与节点板上边缘连接处会出现局部变形，拉支管与主管连接焊缝在靠近节点内侧发生了撕裂。如图4所示。

图4 加劲节点失效模式

偏心相贯节点同样发生主管截面塑性破坏，现象与无偏心节点类似，但在主管与受压支管相贯区域仅一侧出现明显凹陷，另一侧变形不明显，卸载后，压支管向平面外方向发生转动变形。如图5所示。

图5 偏心受力加劲节点破坏现象

2.2.2 荷载-变形特性

试验得到的不同节点的拉支管及压支管的典型轴向荷载-位移曲线如图6所示，节点荷载较小时，支管轴向荷载-位移均呈线性关系，继续增大荷载，支管荷载-位移呈非线性状态，当支管荷载接近节点的极限承载力时，荷载增长缓慢而压支管轴向位移急剧增大，拉支管位移增长则相对缓慢。无偏心相贯节点的支管最大位移略大于偏心节点。

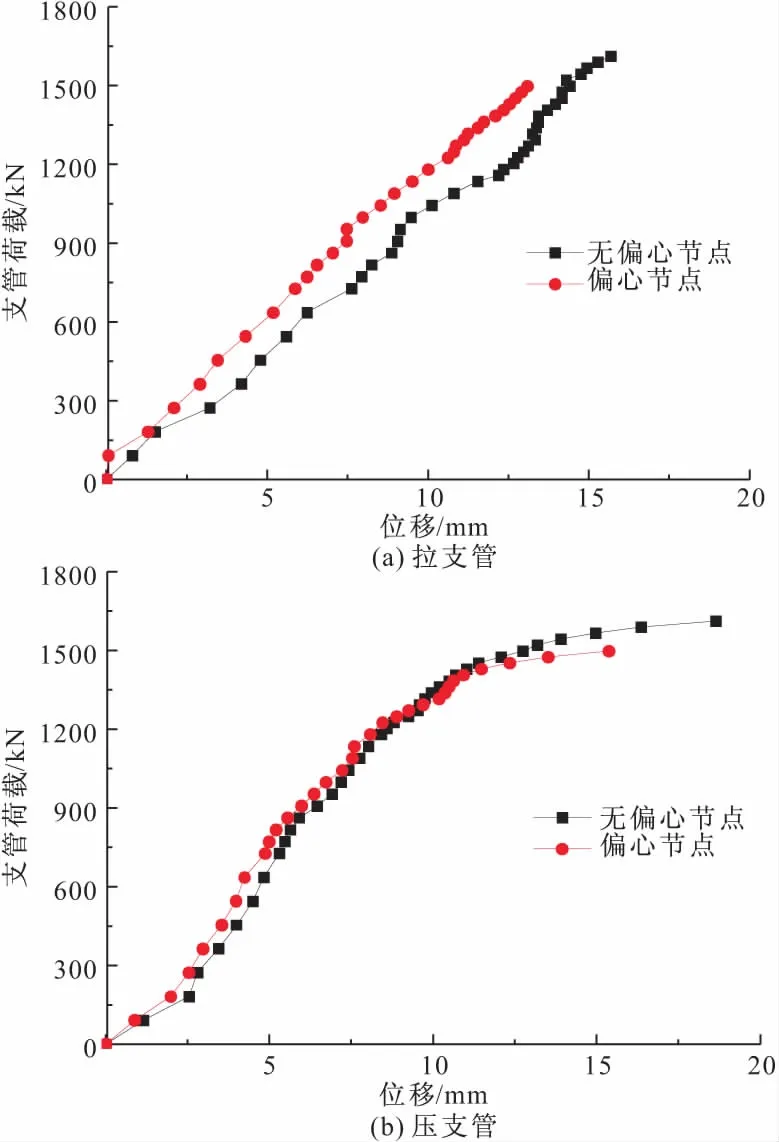
图6 节点支管荷载-位移曲线

图7给出了支管平面外偏心荷载下，压支管端板平面外变形与节点支管轴向荷载的关系曲线。荷载较小时，支管平面外变形随荷载变化较小，当支管荷载接近节点的极限承载力时，支管的平面外变形随着荷载增大而急剧增大，直至节点破坏。

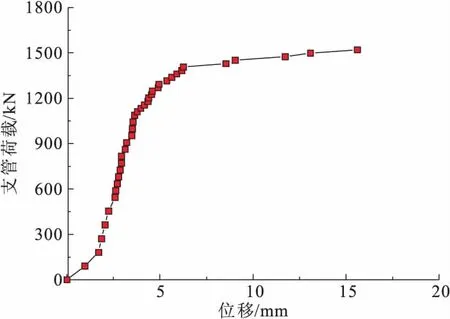
图7 偏心节点支管平面外荷载-位移曲线

2.2.3 典型位置应变分布

受压支管一侧节点典型位置荷载应变曲线如图8所示，拉支管下侧主管侧面为节点主拉应变集中区域，主管轴向拉应变较小，而与主管轴向夹角45°方向拉应变最大，根据应变公式计算，节点主拉应变方向与主管轴向的夹角大约在50°～70°之间。而主管与受拉支管相贯位置呈压应变，节点荷载越大应变发展越快。极限状态下，节点主拉应变区及相贯位置均已完全屈服。特别的，对于支管偏心受力的相贯节点K2，在进入屈服阶段后，节点区塑性变形较大一侧的相贯位置压应变远大于另一侧。

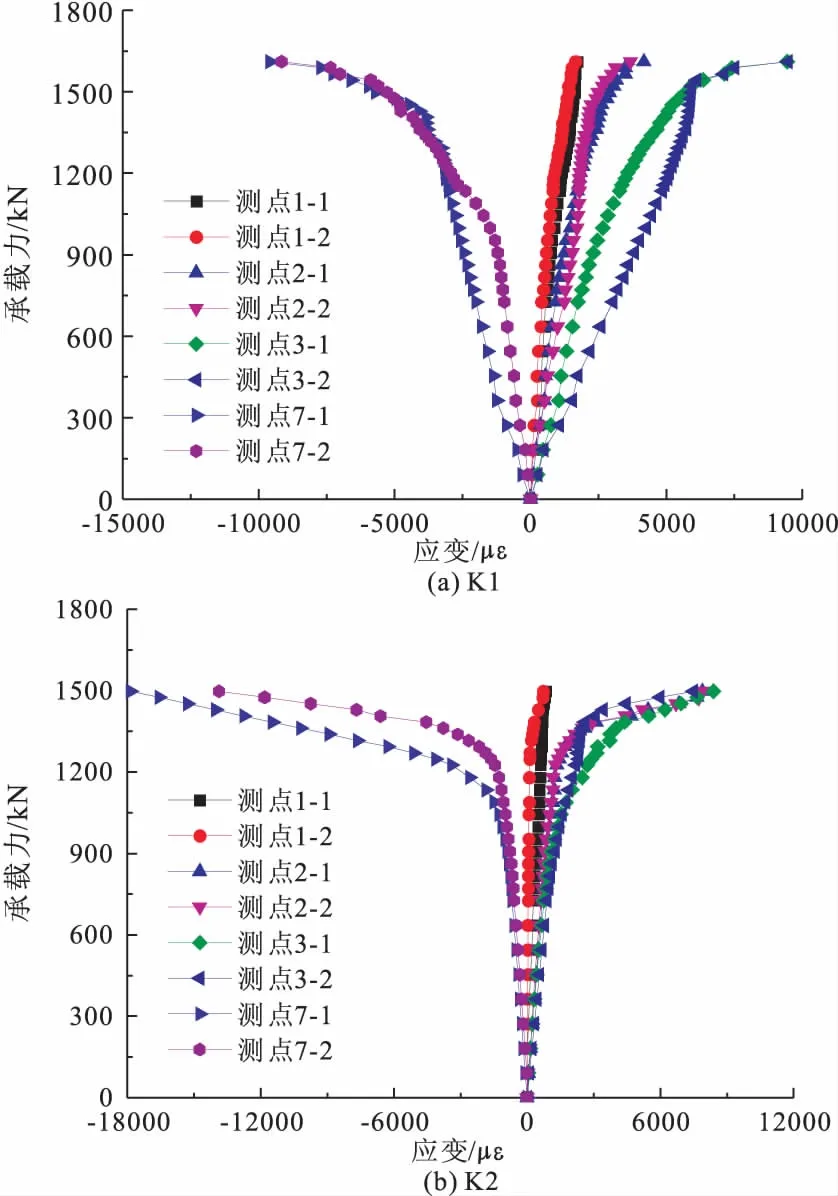
图8 压支管侧荷载-应变曲线

受拉支管一侧节点典型位置荷载应变曲线如图9所示，拉支管下侧主管侧面为节点主压应变集中区域，主管环向压应变较小，而沿主管轴向压应变最大，根据应变公式计算，节点主压应变方向与主管轴向的夹角大约在10°～30°之间。而主管与受拉支管相贯位置呈拉应变，节点荷载越大应变发展越快。极限状态下，节点主压应变区及相贯位置均已完全屈服。特别的，对于支管偏心受力的相贯节点K2，在进入屈服阶段后，节点区塑性变形较大一侧的相贯位置拉应变远大于另一侧。

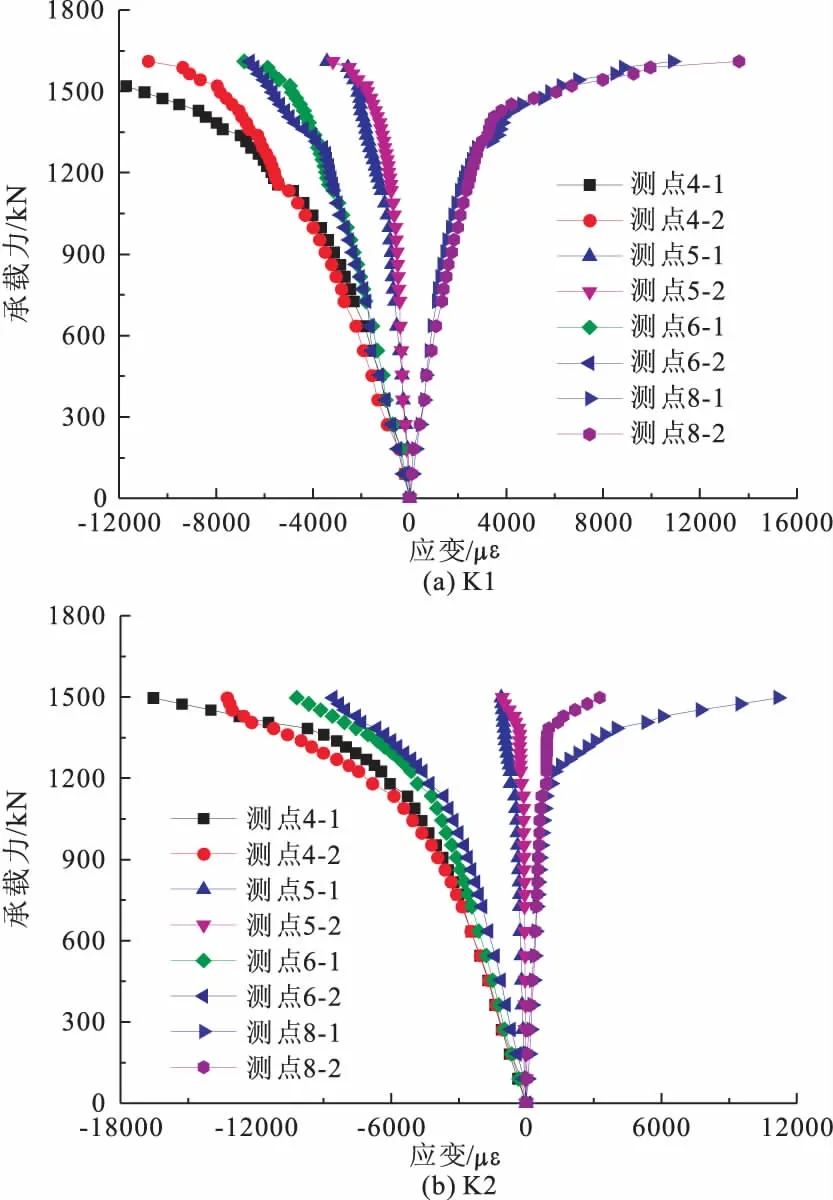
图9 节点荷载-主压应变曲线

2.3 结果分析

根据实验现象及采集到的数据，表3给出了实验节点的最大承载力，最大位移等试验结果。综合比较K1及K2节点的试验结果，两个节点的规格完全相同，但支管偏心受力相贯节点的极限承载力为无偏心节点的93%，可知，压支管偏心荷载会使节点发生平面外变形，并明显削弱K形加劲相贯节点的承载力。

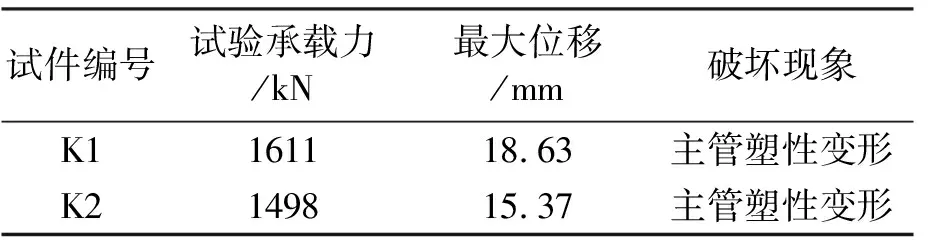
表3 试验承载力及破坏特征

3 节点承载力特性模拟分析

3.1 节点建模

选取试验节点进行建模分析。节点模型如图10所示，节点主管、支管及加劲节点板采用三维8节点shell181单元，主管及支管管端均设置solid45单元的端板，以方便在模拟运算时布置约束及载荷。加载计算时，模型主管一端铰接，另一端及拉压支管端板两侧对除沿轴线方向的其他方向位移进行约束，可以看作在两支管管端各布置一个仅可沿支管轴线方向运动的滑动支座，而对于偏心节点，在压支管端板的平面外方向不设置位移约束，加载轴力对称布置在主管及支管端板上。材料非线性采用增量理论、多线性随动强化准则，几何非线性的求解采用弧长法，采用大变形方法进行计算分析。

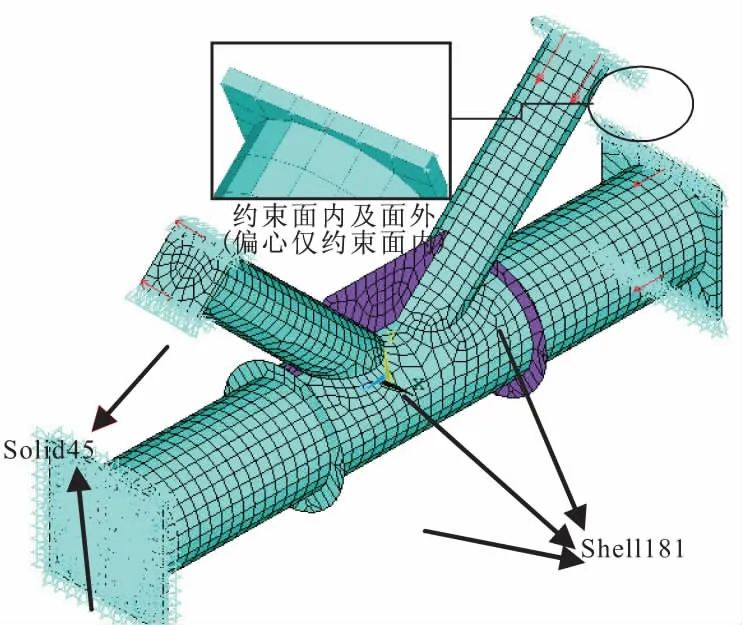
图10 节点有限元模型

3.2 模型分析结果

3.2.1 承载力及荷载-变形特性

如图11所示，K形相贯节点模型在极限状态下，主支管相贯位置发生凹陷，节点区发生塑性变形破坏，而在偏心受力条件下，主管相贯区域一侧发生明显凹陷，另一侧变形不大，同时，压支管向节点平面外发生转动，均与实验现象相符。

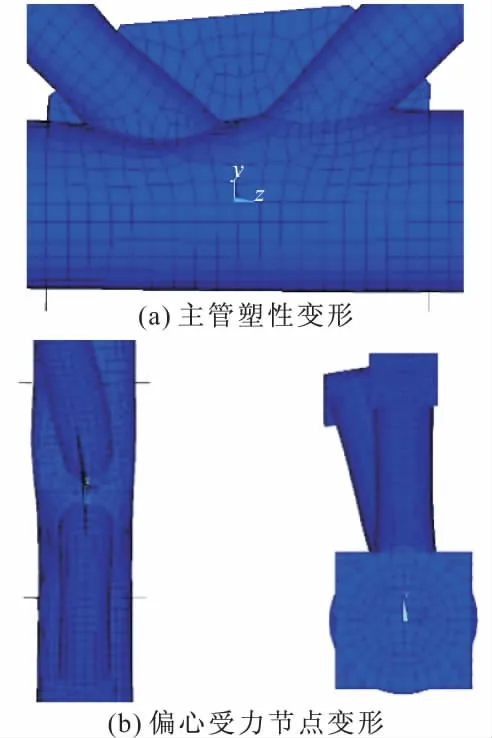
图11 节点模拟变形

有限元分析得到的节点压支管的轴向荷载-位移曲线及偏心节点压支管平面外荷载-位移曲线如图12所示。荷载-位移曲线变化趋势与试验结果类似，相比而言，相同荷载下支管位移的分析结果小于试验值。

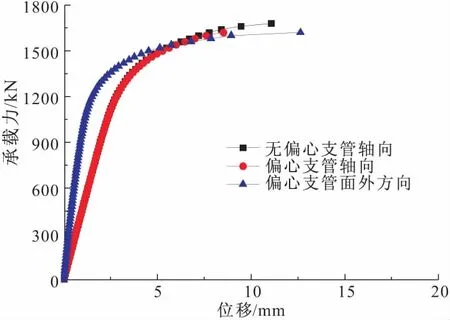
图12 压支管模拟荷载-位移曲线

模拟分析得到的承载力如表4所示，节点模拟承载力略大于试验值，约为试验值的1.0～1.1倍左右。

表4 模拟承载力

3.2.2 节点区应力分布

极限状态下，节点区的拉应力及压应力分布如图13，14所示，根据应力矢量图可知，压支管下方主管侧面为节点主拉应力集中区域，而拉支管下方主管侧面为节点主压应力集中区域，主拉应力方向与主管轴线夹角约在50°～70°之间，主压应力方向与主管轴线夹角约在15°～20°之间。从应力云图来看，极限状态下，节点主应力区及主支管相贯处均出现大范围塑性区域。支管偏心受力节点的应力分布状况及应力方向与无偏心节点相似。上述模拟应力分布特征与试验结果均相符。

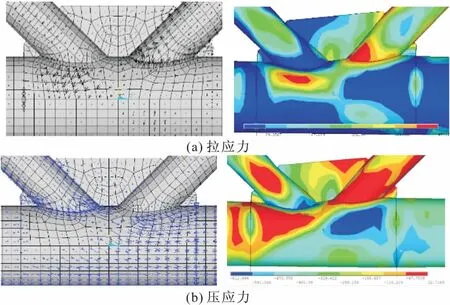
图13 K1节点区应力分布

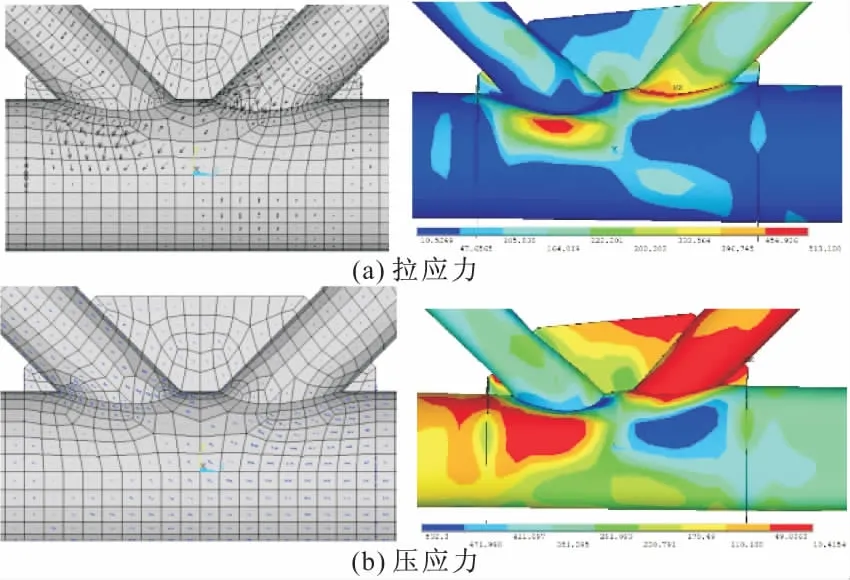
图14 K2节点区应力分布

图15，16给出了偏心节点分别在50%Pu，75%Pu，100%Pu荷载下主管两侧应力分布情况(Pu为节点的极限承载力)，主管变形较大一侧的应力分布及发展明显大于变形较小一侧。

图15 偏心节点拉应力发展

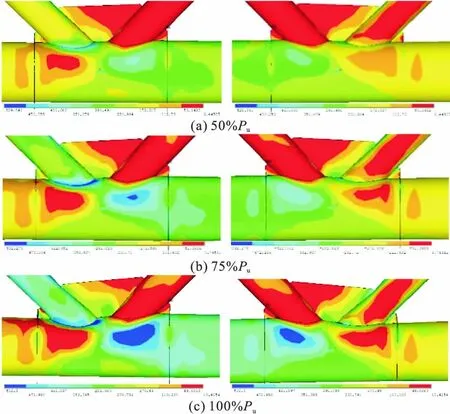
图16 偏心节点压应力发展

综合上述模拟分析结果，有限元分析得到的节点极限承载力与试验承载力非常接近，节点的破坏特征及应力分布发展规律与试验结果也基本相符。证明上述有限元模型是可靠的。

4 压支管偏心受力影响分析

4.1 分析参数

为深入探讨压支管偏心荷载对节点承载力特性的影响，改变偏心受力节点压支管上轴压力的作用位置，研究偏心距对节点极限承载力的影响规律。为使分析结果更加准确，补充了一组K形无加劲相贯节点模型进行分析，节点主支管规格与加劲节点相同。共设置7种不同的偏心距δ，分别为0.001D，0.005D，0.01D，0.025D，0.05D，0.075D，0.1D。

4.2 模拟结果及影响分析

分析获得不同偏心距节点极限承载力及承载力折减率如表5所示。图17则给出了节点承载力折减比例η与支管偏心距δ的关系曲线。由图表结果分析可知，K形相贯节点的极限承载力随压支管荷载偏心距的增大而减小，承载力折减比例与偏心距基本呈线性关系。

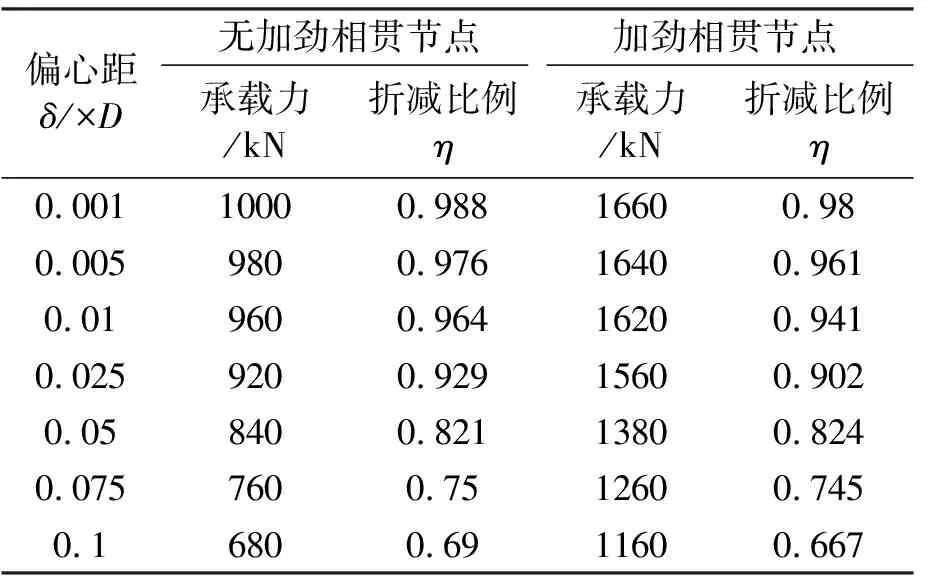
表5 节点压支管不同荷载偏心距对应承载力

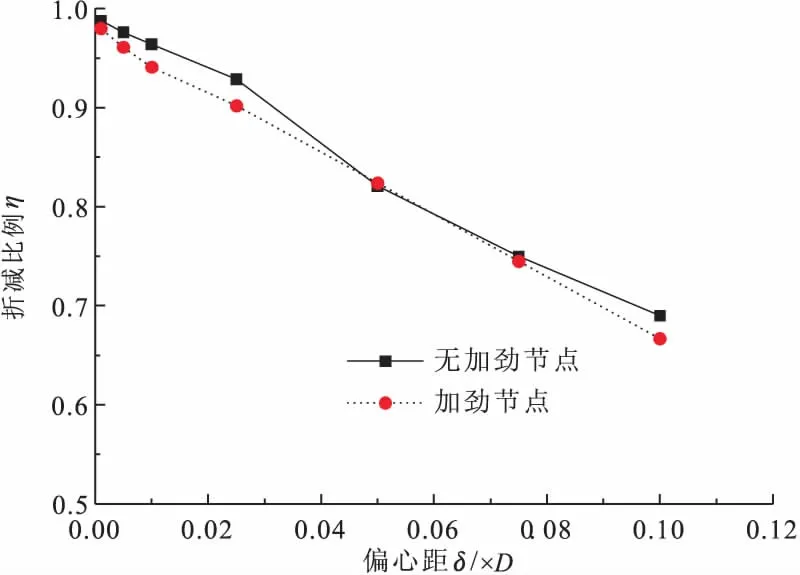
图17 节点偏心距-折减比例关系

依据有限元分析数据，利用最小二乘法对节点承载力折减比例η和偏心距δ关系进行数据拟合，得到支管偏心受力条件下，节点承载力折减比例的建议计算公式：

(1)

利用式(1)得到的承载力折减比例与有限元分析结果的误差均在3%以内，相关系数为0.99987。

实际工程中，由于钢管加工缺陷以及安装误差等原因，节点支管平面外偏心受力不可避免。因此建议实际工程设计时，一方面要加强对K形相贯节点压支管的面外约束。另一方面对于未设置压支管面外约束或约束较弱的K形相贯节点，对原有的设计承载力予以适当的折减，以提高结构的安全性和可靠性，折减比例由工程中具体的偏心距确定。

5 结 论

基于试验研究及理论分析，可以得到如下主要结论：

(1)支管偏心受力时，K形加劲相贯节点主管相贯区域仅一侧发生明显凹陷，支管向节点平面外发生转动；主管变形较大一侧的应力发展明显大于变形较小一侧。

(2)支管平面外偏心受力会使节点发生平面外变形，并严重削弱节点的承载力，其折减比例与压支管荷载偏心距呈线性关系，并给出了节点承载力折减比例的建议计算公式。

(3)实际工程设计时，建议加强对K形相贯节点压支管的面外约束。对于未设置压支管面外约束或约束较弱的K形相贯节点，对设计承载力予以适当的折减，以提高结构的安全性和可靠性。