基于改进滑动窗多项式拟合法的航空器4D航迹预测

张建祥，甘旭升，周志靖， 杨捷

(1.西京学院 理学院，西安 710123) (2.空军工程大学 空管领航学院，西安 710051)

0 引 言

航迹是指航空器在飞行过程中按时间顺序所经历的全部或部分空间位置点的集合，将时间与各个空间点位一一对应后的组合被称为4D航迹。航迹预测是指根据航空器初始飞行计划、历史航迹信息与经验信息，采用相应预测方法，对航空器未来时间段内将要产生的航迹点进行预测。高精度的4D航迹预测是无人机飞行防相撞空中威胁态势预警技术的基础，是提高空中交通管理效率与安全水平的重要技术手段。

卡尔曼滤波是由 R.E.Kalman[1]于1960年推导出来的一种最小方差最优估计算法，主要用于导航系统多传感器信息融合处理和目标状态估计。1998年，L.Tong等[2]首次应用卡尔曼滤波算法解决航迹预测问题，对相邻时刻目标位置及其瞬时速度进行预测，从一定程度上改善了预测精度，但在实际应用中存在非线性系统的适用性问题，预测性能还有较大提升空间。之后，又有诸多研究人员先后提出改进型的基于残差均值的交互式多模型跟踪滤波算法处理航迹预测问题，该滤波算法对机动目标追踪预测有较高精度，但需要做大量的数学建模工作，例如航空器运动模型、运行环境模型等，并最终融合各种模型，形成航迹预测模型，工作量非常巨大[3-6]。此外，引入数据挖掘方法对航空器历史航迹数据进行处理、分析，挖掘数据中隐含的模式，从而预测航空器未来位置，并已在航空器4D航迹预测领域得到应用，比较成熟的方法，例如神经网络算法，存在局部收敛问题和网络结构确定问题。美国艾姆斯研究中心与美国管制员协会联合研发了中央终端区管制自动化系统[7]，其航迹预估模块是核心部分，可生成空域内所有航空器未来30 min内的航迹。PATs[8]是欧洲开发的航迹预测工具，可预先评估所发出的管制指令对航空器的影响，提高欧洲地区空中交通管理效率与安全水平。国内的航空器4D航迹预测研究起步较晚。张军峰等[9]提出了基于连续动态模型与离散动态模型的4D航迹预测方法，并将其用于离场航迹预测，但该方法复杂度较高，无法满足实时性需求；王建忠等[10]根据点融合进近的特点，提出航空器4D航迹预测方法，并采用遗传算法进行求解，但该方法仅能处理简单问题，无法预测多跑道航迹的复杂情况；张振兴等[11]提出基于实时反馈长短期记忆神经网络的4D航迹预测模型，但该方法确定网络参数存在较大难度，所建模型通常无法保证精度。

本文提出采用滑动窗多项式拟合法解决航空器4D航迹预测问题。对滑动窗多项式拟合法进行改进，构建4D航迹预测模型，力求给出一种精度高、简单易行且计算简便的航迹预测方法，并通过实例验证其有效性和可行性。

1 滑动窗多项式拟合预测原理

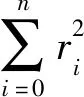
曲线拟合的具体作法：针对给定数据点{Xi|i=0,1,…,n}，在给定的函数类Φ中，求f(ti)∈Φ，使误差ri=f(ti)-Xi(i=0,1,…,n)的平方和最小，即

(1)

从几何意义上讲，就是找寻出一条曲线y=f(t)，使之与给定点{Xi|i=0,1,…,n}的距离平方和为最小。函数f(t)称为拟合函数或最小二乘解，求拟合函数f(t)的方法称为曲线拟合的最小二乘法。

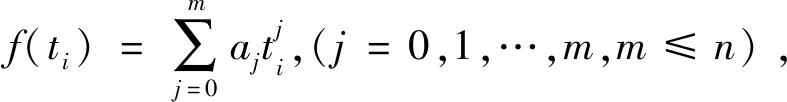
(2)

A=(PTP)-1PTX

(3)

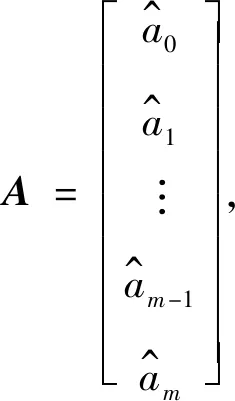
易证式(3)中(PTP)为对称正定矩阵，故存在唯一解。求解式(3)可得拟合多项式

(4)

由式(4)可对(tn+dt)时刻的目标航迹进行预测，即采用多项式拟合法预测航迹：

(5)

固定式(5)中的n值，即预测模型取固定数量的数据点，并随着周期更新，不断接收数据点，剔除相同数量的旧数据点，即在多项式拟合法中应用滑动窗思想，模型将具有动态预测能力。

2 滑动窗多项式拟合法的改进

为了最大程度上利用历史数据信息，提高算法预测性能，对传统滑动窗多项式拟合法提出如下改进措施。

2.1 构建合适多项式拟合方程

传统滑动窗多项式拟合法的优点在于采用递推法最大程度地利用有限的历史数据信息，而本文对滑动窗多项式拟合法的改进之处则是进一步强化了该优点。传统滑动窗多项式拟合法基于历史数据组构建了一个多项式拟合方程，依据该多项式拟合方程计算所有预测值，但每个预测值与历史数据组的时间距离均不同，仅仅依靠同一个多项式拟合方程，并不能完全表达出每个未来值受历史数据组的影响程度。本文在同时预测多个连续未来值时，为每个预测值构造了更为合适的多项式拟合方程，以便更准确地体现历史数据组对每个未来值的不同影响，将得到比传统滑动窗多项式拟合法更高的预测精度。

为每一个预测值构建更合适的多项式拟合方程的关键在于挑选合适的历史数据组，本文基于每个预测值与当前值的时间距离来挑选历史数据组，充分考虑多项式拟合法的时间序列性质。在实际应用中，假设当前值为Xk，滑动窗宽度为n，即预测模型中的历史数据个数为n，预测当前值之后1,2,…,q时刻的未来值，针对当前值之后第s(1≤s≤q)时刻的未来值进行预测时，其与当前值的时间距离为s，则其历史数据组的选择应为{Xk-s(n-1),Xk-s(n-2),…,Xk-s,Xk}，再依据式(5)，即可为每个预测值提供更合适的多项式拟合方程。

2.2 滑动窗多项式参数自适应

本文所提出的滑动窗多项式参数自适应主要是指拟合多项式阶数与滑动窗长度的自适应。

2.2.1 拟合多项式的阶数自适应

根据多项式的最小二乘拟合原理可知，在计算预测模型时，首先要确定拟合多项式的阶数m。要获得高精度的航迹预测值，必须判明目标的运动状态，使拟合多项式的阶数与其相适应。本文将目标运动模式划分为类直线运动与曲线运动，设定目标处于类直线运动模式与曲线运动模式时，对应的拟合多项式阶数m分别为1和2。

对于三维空间中目标的运动模式是否存在类直线与曲线之间的突变以及如何进行突变的判定问题，将其简化到三个单维空间之中进行解决，根据目标在单个维度之中的航迹点绘制时间-位置折线图，取相邻折线所形成角度的大小以及角度的连续变化趋势为判定依据。

在目标航迹序列中取X轴上相邻的四个航迹点为xk-3,xk-2,xk-1,xk，由于具有相同的时间间隔，根据上述四个航迹点可直接绘制成时间-位置折线图，如图1所示，α1为目标在X轴上航迹点xk-3,xk-2,xk-1形成相邻折线的夹角，α2为目标在X轴上航迹点xk-2,xk-1,xk形成相邻折线的夹角。

根据向量夹角公式可得出图1中两个连续夹角的计算方程为[13]

(6)

式中：arccos为三角函数中反余弦符号；‖‖2为向量的2-范数符号[14]。

图1 时间-位置折线图Fig.1 Time-position line chart

可通过设定一个参数λ来进行目标运动模式与相关突变情况的判定：

若目标航迹满足α1>λ,α2>λ，则目标在X轴上处于曲线运动模式，拟合多项式阶数取m=2；若目标航迹满足α1>λ,α2≤λ，则目标在X轴上是从曲线运动模式转为类直线运动模式，拟合多项式阶数取m=1；若目标航迹满足α1≤λ,α2>λ，则目标在X轴上是从类直线运动模式转为曲线运动模式，拟合多项式阶数取m=2；若目标航迹满足α1<λ,α2<λ，则目标在X轴上是处于类直线运动模式，拟合多项式阶数取m=1。

目标在Y轴与Z轴上的运动模式与相关突变情况的判定，与目标在X轴上的判定原理相同，此处不再赘述。

2.2.2 多项式滑动窗长度自适应

因为预测是基于有限的历史数据进行的，所以必须选择所使用时间窗宽度。如果时间窗宽度较大，即历史数据太多，则预测算法的运算量加大，导致预测缓慢，且如果目标运动轨迹变化较快，将导致实际目标运动轨迹与时间多项式函数之间的拟合效果恶化，则预测偏差增加；如果时间窗宽度太小，则数据量过少，所计算出的多项式函数将不能描述目标的运动特性，预测效果也不理想。因此，确定滑动窗宽度时，一方面要考虑不能使预测模型计算太多的历史数据，即滑动窗宽度不可太宽，另一方面则要兼顾目标运动轨迹变化的快慢，即须考虑所选取的拟合多项式阶数。

综上所述，为了进一步减少拟合误差，提高预测精度，依据多项式拟合原理得出拟合多项式滑动窗长度n与阶数m之间的关系式(式(7))，而且在低阶数多项式拟合法的位置预测研究中，李亚宁[12]已通过仿真证明了其合理性。

n=m+1

(7)

3 多项式拟合法航迹预测实现

采用改进的滑动窗多项式拟合法对航空器航迹进行预测，其过程是先在直角坐标系中X,Y,Z轴上分别对航空器航迹进行预测，而后形成对航空器三维空间航迹的总体预测。具体步骤如下：

(1) 按照改进方法在X,Y,Z轴上为每个预测值挑选合适的历史数据组。

(2) 依据式(6)及目标运动模式与相关突变情况的判定结果，确定X,Y,Z轴上的拟合多项式阶数mx,my,mz，滑动窗长度nx,ny,nz。航空器在X,Y,Z轴上的运动轨迹多项式拟合函数为

(8)

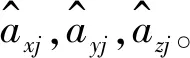
(9)

式中：T为更新周期。

求得式(9)中X,Y,Z轴上航空器航迹预测值，即可得航空器三维空间中航迹总体预测值。

(4) 采用递推算法，重新为每个预测值挑选合适的历史数据组，并利用滑动窗口不断更新最新的X,Y,Z轴上航空器航迹数据，重新确定X,Y,Z轴上的拟合多项式阶数mx,my,mz与滑动窗宽度nx,ny,nz，求得基于线性最小方差估计的多项式预测模型，预测下一周期航空器的航迹。

4 实验仿真与分析

在MATLAB 2014a计算环境中，分析改进滑动窗多项式拟合法预测航迹的性能，并与传统滑动窗多项式拟合法进行对比。由于后者无法自适应调整多项式阶数与滑动窗长度，在仿真分析中，将根据阶数与滑动窗长度不同，设置多个对照组。

4.1 数据来源

实验使用数据来自于通过六阶贝塞尔曲线法构建的入侵机航迹数据，即入侵机相对无人机的航迹数据，如图2～图5所示。在所有的原始数据中，将其中0～99 s的数据只作为历史数据使用，预测航迹为100～196 s中每一时刻的第1～第6步预测值，同时将原始数据中100～196 s的数据作为100～190 s中每一时刻的第1～第6步预测值的对照数据。

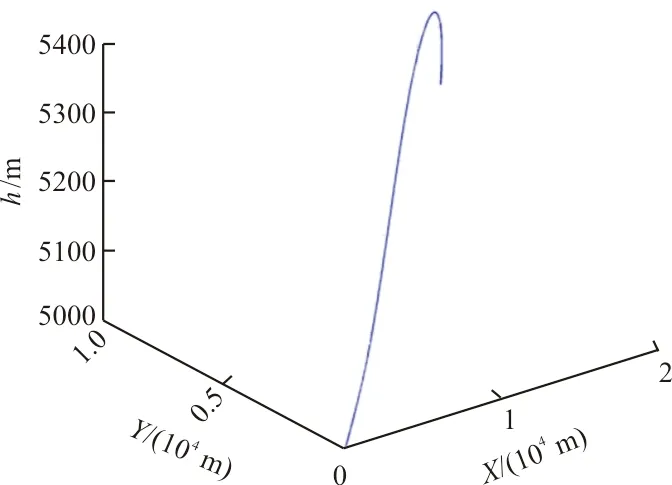
图2 入侵机三维航迹图Fig.2 3D track of the intruder

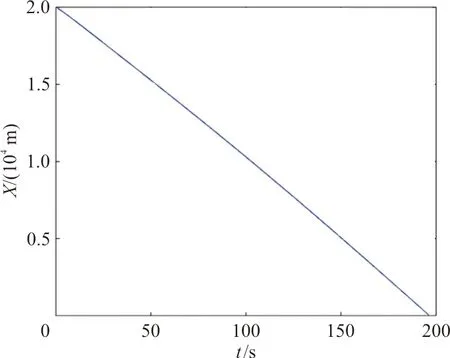
图3 入侵机X轴位置变化Fig.3 X-axis position change of the intruder

图4 入侵机Y轴位置变化Fig.4 Y-axis position change of the intruder

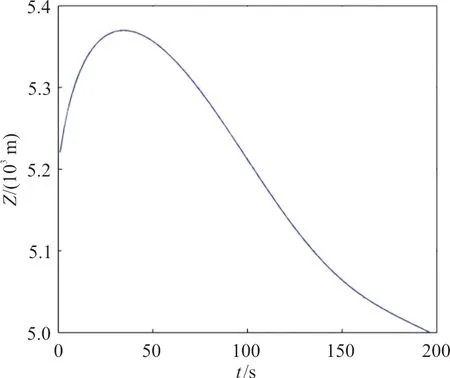
图5 入侵机Z轴位置变化Fig.5 Z-axis position change of the intruder

4.2 参数设置

改进滑动窗多项式拟合法的阶数m与滑动窗长度n，均根据对航空器运动模式的判定自适应取值，令T=1 s，q=6，依据航空器一般性能[15]和多项式预测模型使用经验，对λ取值，设定λ=0.05 rad。

根据传统滑动窗多项式拟合法参数设置的不同，划分四个对照组，为了对比两个改进措施对多项式拟合模型的影响，设定在传统滑动窗多项式拟合法中仅加入参数自适应的改进措施为对照组1。根据经验，将基于传统滑动窗多项式拟合法的其余对照组参数设置为：对照组2，历史数据个数n=2，多项式次数m=1；对照组3，n=3，m=1；对照组4，n=3，m=2。

4.3 误差指标

采用平均绝对误差(mrerr)对航迹预测结果进行分析，统计所有预测时间中每一步预测的绝对误差并取平均值，能直观地表现预测模型的预测性能，计算公式为

(10)

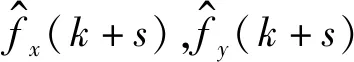
4.4 结果分析

首先，采用改进的滑动窗多项式拟合法，计算航迹数据，根据航迹预测实现步骤及参数设置，得到航空器在100～190 s内每一时刻的第1～第6步预测值，并将预测值与原数据进行比较，计算出绝对误差，并绘制相应的曲线；然后，采用传统滑动窗多项式拟合法，对航迹数据进行计算，并设置参数，得到四组航空器在100～190 s内每一时刻的第1～第6步预测值，计算每个对照组的预测值与原数据的绝对误差，如图6～图10所示，并计算各组中每步预测值的平均绝对误差，如表1所示。

图6 改进多项式拟合法航迹预测绝对误差Fig.6 Absolute error of track predicted by improved polynomial fitting method

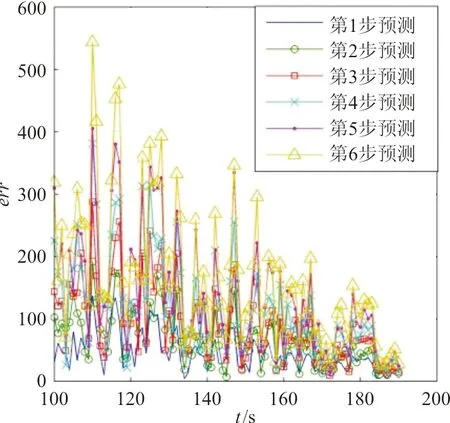
图7 第一对照组航迹预测绝对误差Fig.7 Absolute error of track prediction for first group

图8 第二对照组航迹预测绝对误差Fig.8 Absolute error of track prediction for second group

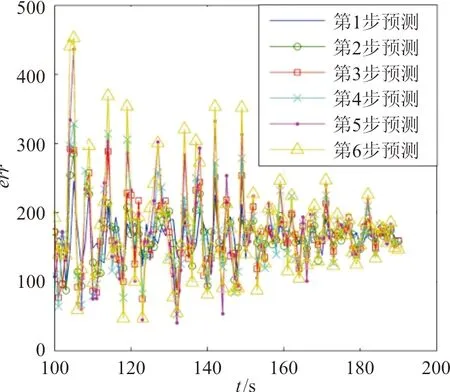
图9 第三对照组航迹预测绝对误差Fig.9 Absolute error of track prediction for third group

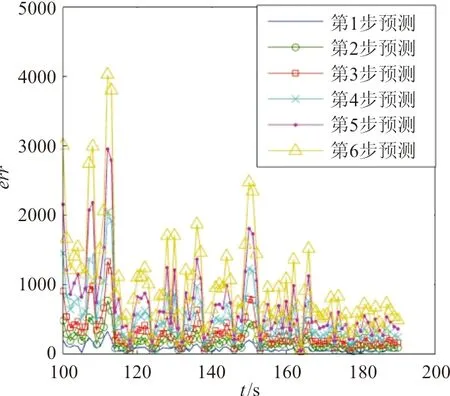
图10 第四对照组航迹预测绝对误差Fig.10 Absolute error of track prediction for fourth group

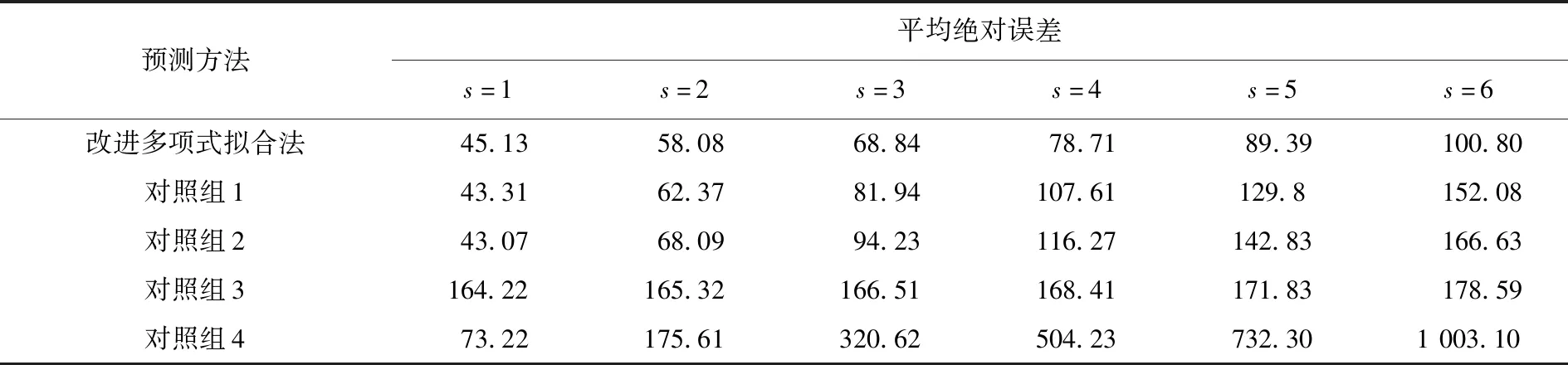
表1 平均绝对误差对比

从图6～图10可以看出：平均绝对误差值在减小，这是由于所加入的噪声方差正比于两机距离。综合分析图6～图10与表1，可以得出：

(1) 本文改进滑动多项式拟合法应用于航迹预测时，其预测精度要优于传统滑动窗多项式拟合法。

(2) 对照组2在第1步和第2步的平均绝对误差与本文改进滑动窗多项式拟合法的mrerr基本相同，但随着预测步数的增加，对照组2中的两个误差指标值具有比改进滑动窗多项式拟合法更大的增加量，表明本文改进方法比传统方法预测性能更加稳定。

(3) 对照组1的mrerr要小于对照组2的，表明在传统滑动窗多项式拟合法中自适应调整多项式参数会得到精度更高的预测值，图7～图8也证明了此结论的正确性；通过对照组1与改进多项式拟合法的mrerr指标值对比，证明了为每个预测值提供更合适的多项式拟合方程的改进措施，提高了航迹预测的精度，图6～图7也证明了此结论的正确性。

(4) 对照组3中的每步mrerr值相对于前一步mrerr值的增长序列与对照组1大体相同，这是由于对照组3与对照组2多项式阶数相同所致，但由于滑动窗长度更大，对照组2中的预测误差均值远大于对照组1。这也印证了式(7)的正确性。

5 结 论

(1) 在使用多项式拟合模型同时预测多个连续未来值时，依据预测值与当前值的时间间隔为预测值挑选历史数据组，为各预测值构造合适的多项式拟合方程，可提高航迹预测精度。

(2) 在单个维度中目标航迹点所构成的时间-位置折线图上，依据相邻折线所形成角度大小及角度的连续变化趋势进行运动模式的判断，实现拟合多项式阶数自适应与滑动窗长度自适应，这样预测的三维航迹精度更高。

(3) 改进滑动多项式拟合法的预测精度优于传统滑动窗多项式拟合法，且进行多步预测时预测性能也更加稳定。未来的研究工作将更多聚焦于本文方法所预测4D航迹在无人机飞行防相撞实践中的验证。