计算成像——全光视觉信息的设计获取

赵巨峰 崔光茫

计算成像——全光视觉信息的设计获取

赵巨峰1,2崔光茫1,2

（1 杭州电子科技大学浙江省装备电子研究重点实验室，杭州 310018）（2 杭州电子科技大学电子信息学院，杭州 310018）

真实世界的视觉光信息是复杂的高维度连续的信号；而现有的数字成像方式是低维耦合离散采集，在成像的各个维度——空间分辨率、时间分辨率、视角及深度、颜色（光谱）等均已达到瓶颈：这极大限制了场景视觉信息的全面获取。计算成像，综合信号处理、光学、视觉、图形学等多学科知识，可突破经典成像模型和相机硬件的局限，以更加全面、精确地捕捉真实世界的视觉信息。文章从计算成像的进化史、计算成像的基本原理、计算成像研究动态、计算成像的关键技术以及计算成像的未来展望等方面，从全光视觉信息的设计获取角度阐述了计算成像的相关概念与理论。

计算成像 全光函数 高维度 计算重构

0 引言

计算成像/计算摄像（computational imaging/computational photography）是近年来受到关注的一个新领域[1]。计算成像能提高信息计算分析的自由度，使得高维度视觉信息在尺度与分辨率上实现质的突破。计算成像相关理论和技术的发展，在宏观与微观层面，都推进了对新现象、新规律观测手段的能力提升。计算成像是计算机视觉、图形学、应用光学、光学成像等领域交叉创新的产物[2]，其基础是传统的光学数码成像。

观测物理世界，光信息是最重要的载体。对视觉光信息的观测，成像历史可以归纳为三次革命。

第一次革命：光学元件，如图1所示。世界上最早的成像在公元前400年，中国的墨子发现了一个小孔的装置就可以成像（小孔成像原理）。现代成像所用的光学成像装置起源于意大利佛罗伦萨。为实现光学成像，当地从业者设计了类似于眼镜的装置（spectacles）。世界上最早的望远镜头的设计图纸如图1所示。第一次成像革命使人们意识到设计各式各样的光学系统与装置可以进行成像，并用眼睛观测，但视频图像无法保存，故无法使用图像处理等现代手段。

图1 成像的第一次革命

第二次革命：光化学和微电子，如图2所示。第二次革命中，成像有了记忆（memory）以记录图像：一是基于光化学的方法（如胶片），二是基于微电子、集成电路的数字成像器件（如CCD、CMOS）。视频图像的记录为进一步的图像处理和分析提供了可能。

图2 成像的第二次革命

第三次革命：计算成像，如图3所示，是基于成像链路与各环节控制的计算成像的产生。成像技术发展到现在，计算成像可以让研究者更早地介入成像的过程，对于处理图像时无法实现的指标，可以在成像的过程中就加入一些“计算”和“智能”的因素，通过控制成像链路与环节，实现特殊的观测目的。

在过去的近百年里，各国的研究者对视觉光信息从空间、角度、频谱（光谱）、时间等各个维度进行了观测，谱写了百年诺贝尔科学奖的辉煌，如表1所示。通过显微镜等的研究，突破宏观与微观的空间尺度上的局限；利用光谱仪等研究设计，不断提升光谱观测范围与分辨率；从全息、飞秒光谱等角度，拓展了观测维度；CCD的发明使得光信息的计算成为了现实。研究者认为，光信号是一种高维度信息，是可分维、可计算的。随着人类不断的研究与拓展，观测维度持续增加，观测范围、分辨率不断扩展。人类在单一维度的观测已经经历了革命性的发展，但人们对物理世界的高维度高分辨率的观测追求永无止境。

图3 成像的第三次革命

表1 与光信息探测相关诺贝尔自然科学奖（物理/光学）

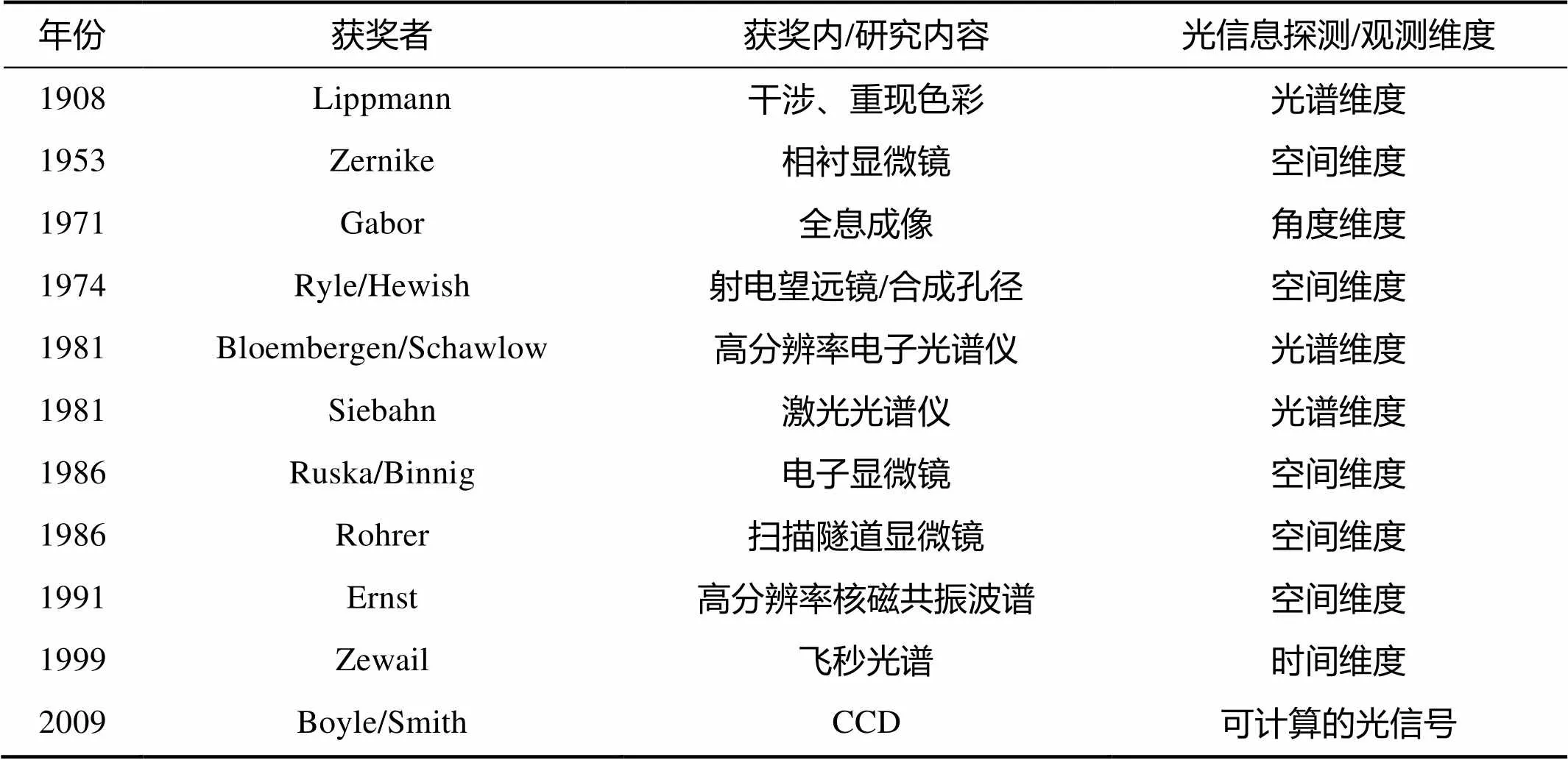
Tab.1 Nobel Prize in natural science related to optical information detection（physics/optics）

鉴于经典成像方法在成像的各个维度——空间分辨率、时间分辨率、视场及深度、光谱/颜色等层面的研究均已达到瓶颈，计算成像应运而生。21世纪初，计算成像学由斯坦福大学、哥伦比亚大学、麻省理工学院等大学的研究者共同发起并探索，旨在打破传统数码/数字成像中先采集后处理的模式，在信号相关理论基础上有机结合采集与后处理，实现高维度视觉光信息的耦合采集与重构重建。清华大学戴琼海院士等将计算成像定义为[3]：一门将计算机视觉、数字信号处理、图形学等深度交叉的新兴学科，旨在结合计算、数字传感器、光学系统和智能光照等技术，从成像机理上来改进传统相机，并将硬件设计与软件计算能力有机结合，突破经典成像模型和数字相机的局限性，增强或者扩展传统数字相机的数据采集能力，全方位地捕捉真实世界的场景信息。计算成像应运而生是不同领域发展碰撞的结晶，是一门交叉创新学科，如所图4所示。计算成像的产生与发展能够突破经典成像模型和相机硬件的局限，更加全面、精确地捕捉真实世界的视觉光信息。

计算成像理论与关键技术的核心在于如何革新成像机制与系统，耦合采集视觉信息，表征场景属性，突破当前成像局限，扩大后处理分析的空间，最终可捕获高维度高分辨率的光信息，实现场景目标信息与本质特性的高精度高效观测。

图4 计算成像的学科衍生与交叉

1 计算成像的基本原理

光信号在不同领域有不同的描述方式，如应用光学、物理光学与波动光学、傅里叶光学等都有对应的描述模式，而计算成像的原理基础是基于全光函数的视觉信息描述。

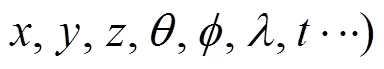
图5 视觉系统采集基于全光函数的场景信息

我们可以认为，使用七维全光函数()+强度对光线进行描述：在时刻从三维空间任意位置（,,），沿着方向（,），观察到波长为、强度为|(,,,,,,)|的光线。基于全光函数，可将富含场景信息的光信号更完整地耦合采集与重构以获取高维度、高效、高精度观测。

基于全光函数，利用现有技术与创新技术，充分挖掘各个维度的观测潜能。通常是以牺牲一种或数种维度来提升另一种或数种维度的观测性能，如“以空间换时间”的思路等，以此来实现计算成像功能。

当前，成熟的数码成像模式可与计算成像相比，前者通常包含两个步骤：一是相机采集图像，二是后期处理即数字图像处理；而计算成像，是为了某个特殊观测目的与问题，去控制成像过程，协调硬件与软件，通过计算获取最终的视觉图像。传统数码成像与计算成像的区别如图6所示，该图简明清晰概括了计算成像的原理与技术基础。

图6 传统数码成像与计算成像的原理与技术综合对比

2 计算成像的发展态势

计算成像的发展，是基于全光函数的各个维度的观测，甚至更多附加维度的观测。在近些年的研究中，相对于图像后处理，计算成像的论文并不是很多，主要是由于计算成像涉及到硬件系统，与传统的图像、视频处理技术在获得数据后再处理不同，计算成像会更早的介入成像链路，研究周期相对长，也更困难些。

目前，如图7所示，国际上诸如麻省理工学院、斯坦福大学、卡内基梅隆大学等学校都开设了计算成像相关课程，同时国际上也有诸多实验室专注于该技术的研究，如斯坦福大学的SCI实验室、麻省理工学院的Media Lab、杜克大学等。国内清华大学、南京大学、北京理工大学、中国科学技术大学、北京航空航天大学、西安电子科技大学、杭州电子科技大学等高校以及中国科学院等科研院所也开设了相关的教学课程或开展了相关的研究工作。

图7 国际计算成像/计算摄像实验室

计算成像已经发展了10余年，国内外的研究单位与企业为获取全光视觉信号，构造装置并搭建平台，致力于维度采样的设计与优化，例如，斯坦福大学研制的可编程配置的Franken相机[4-5]、清华大学搭建的变光照三维相机阵列光场采集系统[6-7]等，这类系统为本领域的基础理论与实际应用的发展奠定了实验研究基础。市场上已经出现基于本技术的产品，例如先成像后对焦的光场相机[8-10]Lytro的1代和2代（图8）、具备高精度的微几何快速测量的变光照弹性传感相机GelSight/GelSlim[11-12]等。

图8 Lytro的1代和2代光场相机

本节将从全光函数的维度出发，即从空间、时间、角度、光谱（频谱）、其他维度等层面，分析计算成像的发展脉络与动态。

2.1 空间维度

成像系统在空间维度的采样是最为人所熟悉的，面对的是全光函数中的三个维度，其投影到维度上即经典成像采样。在的采样在深度测量分析、三维重建、对地对天观测等都有非常重要的应用意义。

经典成像中投影到上，影响几何信息的采集，计算成像旨在解决该问题。

一方面，可以对光照进行控制及优化计算，实现场景本质信息耦合于光信号上，通常使用的是两类方式：一是基于变化光照的系统（可控制时间、光谱、强度等），一般使用球状光台式样[13-17]；二是基于控制数字光处理器（digital light processor，DLP）的结构光系统[18-19]。利用场景的光路计算，可实现高精度的下的三维重建、材质的鲁棒重建与深度信息获取等。如图9所示，基于几何与光照的迭代优化，多光照及多视角的三维重建可以实现很好的重建效果[20-21]。在光台系统下，使用极化球面梯度光照克服高光影响而获得高精度的人脸几何信息[22-23]；此外，连续球面谐波光照的计算可以辅助优化高光/透光等复杂材质作用下的三维重建[24-25]。利用结构光，可实现稳定的距离检测[26-28]，达到精确的几何重构[29- 30]。此外，研究者利用压缩结构光法提出了一类非均匀介质恢复方法[31]。

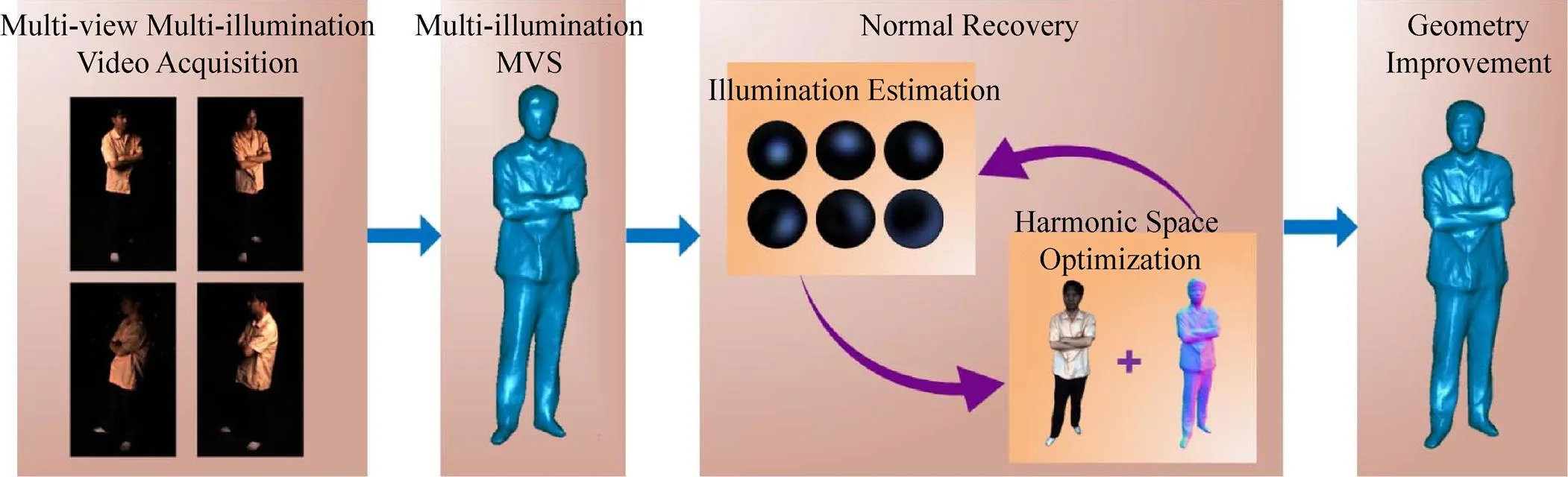
图9 基于多光照及多视角的xyz维重建

成像系统的空间分辨率是空间维度的最直接体现。杜克大学Brady等机构，在DARPA资助下，开展了AWARE1和AWARE2项目，提出并成功实现了十亿像素级相机[32-33]，如图10所示。该成像系统的球形主透镜与微相机阵列克服了经典模式下的几何畸变等缺陷，解决了光容量与像素容量的有效匹配。此外，利用传感器的亚像素级的抖动能实现高分辨率的视频捕捉[34-35]，大量的超分辨率求解也是属于这个范畴的[36-38]。

图10 10亿级像素的高分辨率成像

2.2 时间维度

在时间维度上，通常认为是对采集过程中的时间进行控制（慢速成像下），或者是快速成像如“飞秒”成像等（成像速度与光速相当）。

对于快速成像，有不少研究者开展了研究。麻省理工学院的 Harold Edgerton发明了基于频闪光照捕捉高速事件瞬间的成像技术[39-40]。Veeraraghavan等结合了稀疏重构技术，提出了计算编码频闪光照方法[41]，仅需单个普通相机即可实现周期性高速运动场景的高帧率计算成像。

慢速成像状态下最典型的手段为编码曝光技术[42-45]。为解决场景中物体运动而产生的成像模糊，麻省理工学院的Raskar等人首次提出了编码曝光成像技术，通过相机快门的快速开关过程，在时间轴上定义了一种宽带滤波器，有效保留了场景中的高频信息，使得模糊图像的点扩散函数（PSF）频谱不含零点，原本病态的图像复原成为一个良态问题[46]。

对于传统的成像曝光模式，在曝光时间内获得的图像，相当于一个时间域上的盒状滤波器与图像的卷积，传统成像曝光模型如图11（a）所示，将其转化到频域中，得到其傅里叶变换的幅值曲线如 图11（b）所示。可以看到，幅值曲线在频域上有很多的零点。若采用逆滤波算法复原，其频率幅值作为分母，会将图像中的噪声和振铃放大，严重影响复原结果。

图11 传统曝光模式

与普通相机在曝光期间快门一直处于打开状态不同，编码曝光成像技术通过预先设置的二进制编码序列快速地开关相机快门，如图12（a）所示。编码曝光将成像过程变为一个宽带滤波器与清晰图像进行卷积，有效保护了获取图像的高频信息，避免了点扩展函数出现频域零点，对应的傅里叶变换曲线如图12（b）所示。可以看出，编码曝光得到的频谱图中没有零点，可以使用直接逆滤波的方法来得到复原的图像，使得频域零值放大的情况得到缓解，一定程度上使得图像复原改善成为一个良态的问题。

图12 编码曝光模式

编码曝光成像技术有效解决了病态问题。图13所示为曝光实验示意图，拍摄场景如（a），（b）、（c）分别为通常复原结果与编码曝光状态下的复原结果。由于经典矩形卷积函数的频谱有多个零点，对应于原图像的高频信息损失大，严重的振铃效应是图像复原的必然副作用。然而，编码曝光可设计使得卷积函数频谱没有零点，从而恢复图像时可以保留原图像的高频信息。

图13 编码曝光示意图

2.3 角度维度

角度维度的成像，包含在光场成像中，以采样不同入射角度的光线信号，实现从光照、材质获取与建模、重聚焦（自由聚焦）、光照显示等应用。

光场相机能采集二维角度。一方面，可通过微透镜阵列将不同角度的空间光线映射到不同的传感器像素上（宏像素），牺牲空间分辨率以换取角度分辨率[8, 47-48]。光场成像不需要调整对焦平面[49-50]，有研究者在显微成像上也实现了光场获取实现不对焦[51-52]，并可从不同角度观察样本。另一方面，有研究者基于光圈编码以及掩膜方式实现光场获取。光圈编码是将视角微元化，基于视角复用采集等[53-54]，掩膜思路则是将高维度光场信息转换到传感器的低维频域空间，进而计算解调[55-57]。掩膜法灵活、空间分辨率高，但光通量降低导致能量小。现阶段设计的光场成像系统/相机通常是聚焦全光的，在聚焦全光照相机中，主镜头的聚焦面并不在微透镜阵列/微镜头阵列上，而是在其前或后，如图14所示[58]。采用这种方式，从光路分析上看，微透镜的每个子镜都能将景物经主镜头上的图像呈现在成像传感器上[59-61]，耦合采集得到高的空间分辨率。

2.4 光谱（频谱）维度

自然场景的视觉光信号的光谱/频谱是连续函数，而物体材质的光频谱响应函数是重要的特性表征。HVS只能接收到可见光，而最初以模拟人眼为目标的相机光谱响应函数也类似人眼的三个视锥，即RGB三个通道。计算成像的目标不仅仅局限于逼近HVS，对380~780nm波长的可见光信号能够高精细的采样。

通常将获得光谱图像的设备称为光谱成像仪。光谱分辨率是该设备的重要参数之一，指能够分辨的最小波长间隔。通常，光谱成像按分光方式可分为色散型和干涉型。在计算成像中，希望借助新手段，获取更高的光谱分辨率、空间分辨率、时间分辨率的光谱图像。Mohan等研究者利用衍射光栅将光色散为连续光谱，关键在于他们在光路中加入了掩膜以实现光谱的调制，可实现高动态范围成像[62]，这种方式发展迅速[63-65]。为了获取光谱视频，文献[66]提出棱镜掩膜式光谱视频采集方法，并构建了原型系统（如图15左所示），以在短曝光时间内实现高光谱分辨率的信息采集，以空间换光谱而不牺牲时间；针对棱镜掩膜式光谱视频采集中空间分辨率过低的问题，又设计了混合相机式高分辨率光谱视频捕获方法[67-68]和系统（如图15中所示），解决了光谱视频采集中高光谱分辨率和高空间分辨率同时获取的难题：相关研究的发展也非常迅猛[69]。

美国杜克大学的课题组基于色散型成像光谱仪，用编码孔径代替了狭缝，设计了一套经典的编码孔径快照光谱成像系统（coded aperture snapshot spectral imaging，CASSI system）[69]，其架构图、实物图如图16所示。面向场景，CASSI系统只需一次成像，即将光谱数据立方体压缩为二维图像，从而获得了压缩光谱图像，采用优化重构算法，便可以获得该光谱数据立方体。

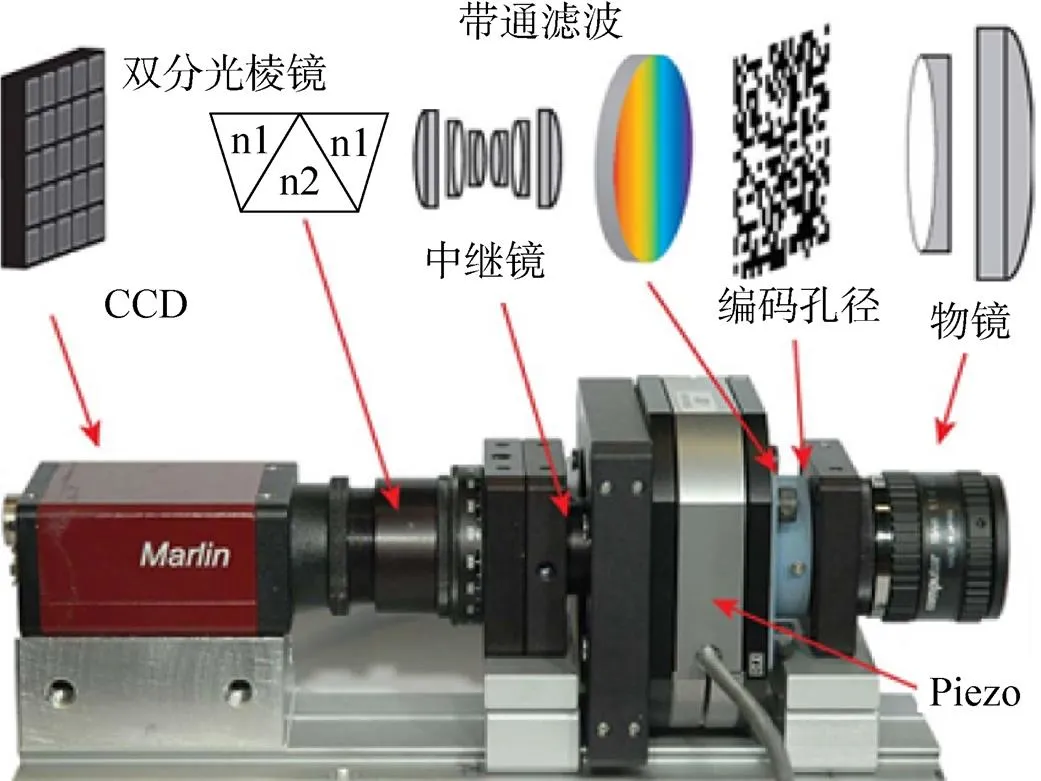
图16 CASSI架构图和CASSI实物图

2.5 其他维度

除了七维全光函数，其他维度如偏振特性、动态范围与极化的研究，以及其他逐渐充实的维度与研究层面，也会进一步壮大装点计算成像这棵大树。

3 计算成像的关键技术

计算成像理论与技术的核心关键在于，如何基于已有硬件基础，创新设计与组装新的方式，有效实现基于全光函数的各个维度的计算采集，以拓展维度的观测范围与精度、速度。

如何利用现有基础，挖掘高维度耦合采集的潜力。前面已经提到，对于场景，视觉系统接收的是基于全光函数描述的高维度视觉信号，而当前的硬件基础架构对信息采样是非常有限的，如图17所示为经典成像模型，其仅仅在二维空间尺度（）具有高采样能力，即仅在（）二维上具有高空间分辨率，其他大部分维度都因积分而采样能力极低：深度维度层面，被投影到（）平面而损失掉了；角度信息（，）也经透镜而积分，无法区分；在光谱采样上，仅仅采用RGB三通道采样，光谱谱线相对粗糙，是非常离散的采样；在时间维度，在每一帧或者每一个曝光时间段内光通量积分，无法辨别这个过程中的变化；至于其他的附加维度，如偏振等，更无法获取。总体而言，经典成像方式是低维度耦合离散采样过程。场景的高维度连续视觉光信号，被采样得到低维耦合离散信号，通过先验知识辅助的后处理，可以适当提升分辨率，但无法弥补已经缺失的信息。而计算成像可从本质上突破现有成像模型的局限性, 将计算引入成像过程, 对光信号进行优化耦合采集, 使得计算重构能够突破传统信号处理的极限, 实现真实光信号的高维度高分辨率计算成像。

因此，计算成像正是要解决这个问题，基于全光函数，创新设计与组装现有硬件基础，可将富含场景信息的光信号更完整地耦合采集与重构获取高维度高效高精度观测。

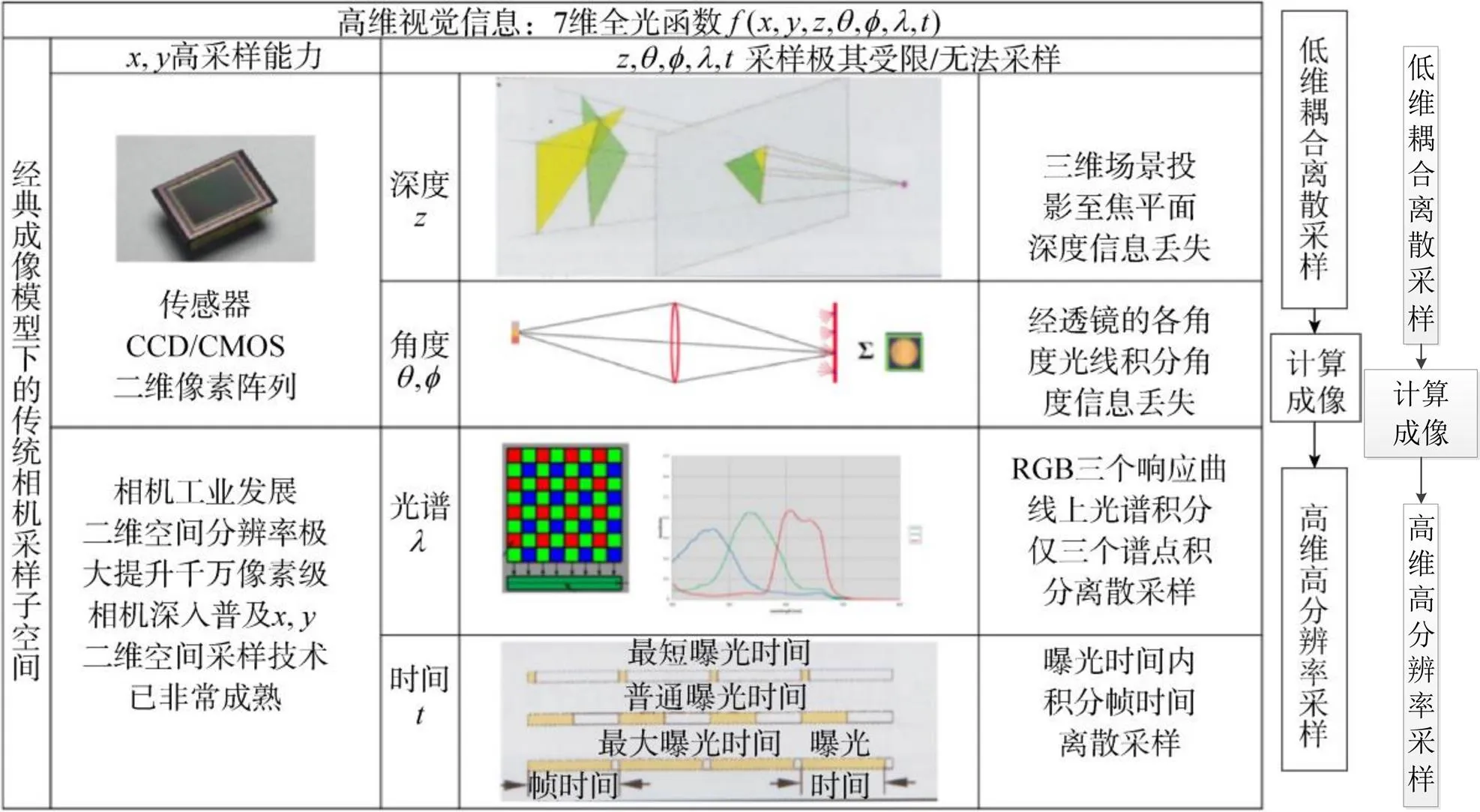
图17 经典成像模型下高维度视觉信息的低维离散耦合采样以及计算成像的突破

传统的胶片或数字图像只是全光函数的一个子集或者切片；计算成像的关键技术在于如何结合光照、光学系统/镜头、图像传感器与电路架构、计算等的控制与协作，硬件与软件链路考虑，改造或改变现有的成像元件与设备，从成像机理上来改进传统成像系统，为更好地采集获取基于全光函数的一个或几个维度的信息，可牺牲其他维度以提升目标维度，实现跨越现有数字数码成像的障碍，使“看不见的内容看得见”，“看不清的内容看得清”，“看不全的内容看得全”，突破经典成像模型和数码成像系统的局限性，全方位地捕捉真实世界的场景信息。

4 未来展望

计算成像是为了克服传统光电成像存在的固有问题而产生的，并且人类对光电载荷的要求越来越高：要求看得越远、越高、越小。计算光学成像是集光学、信号处理和数学于一体的新兴交叉学科，系统地以全局观点来描述成像而实现人类的迫切需求，将是计算成像发展的必然之路。计算成像的未来是光明的。另外，计算成像系统的体积、质量、功耗和成本等问题将是未来发展的要点，革新新机制新元件新系统，形成面向不同信息获取目的的高维度耦合信息获取手段，建立起新型的面向未来的兼容的成像模型。

致谢：感谢浙江省装备电子研究重点实验室的设备与技术支撑。

[1] 索津莉, 刘烨斌, 季向阳, 等. 计算摄像学: 核心、方法与应用[J]. 自动化学报, 2015, 41(4): 669-685. SUO Jinli, LIU Yebin, JI Xiangyang, et al. Computational Photography: Keys, Methods and Applications[J]. Acta Automatica Sinica, 2015, 41(4): 669-685. (in Chinese)

[2] 戴琼海, 索津莉, 季向阳. 计算摄像学: 全光视觉信息的计算采集[M]. 北京: 清华大学出版社, 2016. DAI Qionghai, SUO Jinli, JI Xiangyang. Computational Photography: Computational Capture of Plenoptic Visual Information[M]. Beijing: Tsinghua University Press, 2016. (in Chinese)

[3] 戴琼海, 陈熙霖. 计算摄影学[J]. 中国计算机学会通讯, 2012, 8(8): 1-2. DAI Qionghai, CHEN Xilin. Computational Photography[J]. Communications of CCF, 2012, 8(8): 1-2. (in Chinese)

[4] ADAMS A, JACOBS D E, DOLSON J, et al. The Frankencamera: An Experimental Platform for Computational Photography[EB/OL]. [2019-03-04]. https://docplayer.net/45981202-The-frankencamera-an-experimental-platform-for- computational-photography.html. DOI:10. 1145/2366316.2366339

[5] SENGUPTA S, AMIR T, GALUN M, et al. A New Rank Constraint on Multi-view Fundamental Matrices, and Its Application to Camera Location Recovery[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). New York: IEEE, 2017.

[6] LIU Yebin, DAI Qinghai, XU Wenli. A Point-cloud-based Multiview Stereo Algorithm for Free-viewpoint Video[J]. IEEE Transactions on Visualization & Computer Graphics, 2010, 16(3): 407-418.

[7] DENG Yue, LIU Yebin, DAI Qinghai, et al. Noisy Depth Maps Fusion for Multiview Stereo via Matrix Completion[J]. IEEE Journal of Selected Topics in Signal Processing, 2012, 6(5): 566-582.

[8] REN N, LEVOY M, BREDIF M, et al. Light Field Photography with a Hand-held Plenoptic Camera[EB/OL]. [2019-03-04]. https://www.docin.com/P-229816634.html.

[9] REN N. Fourier Slice Photography[EB/OL]. [2019-06-15]. http://graphics.stanford.edu/papers/fourierphoto/fourierphoto- 600dpi.pdf.

[10] LESSIG C. Local Fourier Slice Photography[EB/OL]. [2019-05-04]. https://arxiv.org/pdf/1902.06082.pdf.

[11] JOHNSON M K, COLE F, RAJ A, et al. Microgeometry Capture Using an Elastomeric Sensor[EB/OL]. [2019-06-16]. https://www.researchgate.net/publication/220183942_Microgeometry_Capture_using_an_Elastomeric_Sensor?_sg=S6laWI-kMrptsxTmh1XDV_8ZlKO3I1YoVwu_1q6NID7wtwlmR13wt271ZeBBwTZwCGSlBrV3AdZ-chZ9i3zSxQ.

[12] DONLON E, DONG S, LIU M, et al. GelSlim: A High-resolution, Compact, Robust, and Calibrated Tactile-sensing Finger[EB/OL]. [2019-05-04]. https://arxiv.org/pdf/1803.00628.pdf 2018.

[13] DEBEVEC P, WENGER A, TCHOU C, et al. A Lighting Reproduction Approach to Live-action Compositing[J]. ACM Transactions on Graphics, 2002, 21(3): 547-556.

[14] HOLM J, MAIER T, DEBEVEC P, et al. A Cinematographic Spectral Similarity Index[C]//SMPTE 2016 Annual Technical Conference and Exhibition. New York: IEEE, 2016.

[15] WENGER A, GARDNER A, TCHOU C, et al. Performance Relighting and Reflectance Transformation with Time-multiplexed Illumination[J]. ACM Transactions on Graphics, 2005, 24 (3): 756-764.

[16] WU Di, LIU Yebin, IHRKE I, et al. Performance Capture of High-speed Motion Using Staggered Multi-view Recording[J]. Computer Graphics Forum, 2012, 31(7): 2019-2028.

[17] LI Guannan, WU Chenlei, STOLL C, et al. Capturing Relightable Human Performances under General Uncontrolled Illumination[J]. Computer Graphics Forum, 2013, 32(2): 275-284.

[18] ELAHI A, SHAHABADI M. A Grating-optic-less Visible Spectrometer Using Fresnel Zone Plate Patterns on a Digital Light Processor[J]. IEEE Sensors Journal, 2018, 18(15): 6432-6437.

[19] HORCHANI R. Femtosecond Laser Shaping with Digital Light Processing[J]. Optical and Quantum Electronics, 2015, 47(8): 3023-3030.

[20] WU Chenglei, LIU Yebin, DAI Qionghai, et al. Fusing Multiview and Photometric Stereo for 3D Reconstruction under Uncalibrated Illumination[J]. IEEE Transactions on Visualization & Computer Graphics, 2011, 17(8): 1082-1095. DOI: 10.1109/TVCG.2010.224.

[21] DAI Qionghai, LI Guannan. Method and System for Free-view Relighting of Dynamic Scene Based on Photometric Stereo: US8928734[P]. 2015.

[22] GHOSH A, FYFFE G, TUNWATTANAPONG B, et al. Multiview Face Capture Using Polarized Spherical Gradient Illumination[J]. ACM Transactions on Graphics, 2011, 30(6): 1-10.

[23] DEBEVEC P E, GHOSH A, FYFFE G. Multiview Face Capture Using Polarized Spherical Gradient Illumination: US9123116[P]. 2012-10-25.

[24] TUNWATTANAPONG B, FYFFE G, GRAHAM P, et al. Acquiring Reflectance and Shape from Continuous Spherical Harmonic Illumination[J]. ACM Transactions on Graphics, 2013, 32(4): 109. DOI: 10.1145/2461912.2461944.

[25] PAPAS M. Recent Advances in Facial Appearance Capture[J]. Computer Graphics Forum, 2015, 34(2): 709-733.

[26] CHEN Tongbo, LENSCH H P, FUCHS C, et al. Polarization and Phase-shifting for 3D Scanning of Translucent Objects[C]// 2007 IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2007.

[27] ZHANG Li, NAYAR S. Projection Defocus Analysis for Scene Capture and Image Display[J]. ACM Transactions on Graphics, 2006, 25(3): 907-915.

[28] FICKLER R, BOUCHARD F, SIT A, et al. Experimental Quantum Cryptography in Laboratory, Long-distance and Underwater Conditions Using Structured Light[C]//Quantum Technologies and Quantum Information Science, February 27 - 28, 2018. Barcelona, Spain: International Society for Optics and Photonics, 2018: 10803: 108030T.

[29] GUPTA M, AGRAWAL A, VEERARAGHAVAN A, et al. Structured Light 3D Scanning in the Presence of Global Illumination[EB/OL]. [2019-06-22]. https://www.researchgate.net/publication/224254728_Structured_light_3D_scanning_ in_the_presence_of_global_illumination.

[30] GUPTA M, NAYAR S K. Micro Phase Shifting[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition. New York, USA: IEEE, 2012.

[31] GU Jinwei, NAYAR S K, GRINSPUN E, et al. Compressive Structured Light for Recovering Inhomogeneous Participating Media[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(3): 555-567. DOI: 10.1007/978-3-540- 88693-8_62.

[32] COSSAIRT O S, MIAU D, NAYAR S K. Scaling Law for Computational Imaging Using Spherical Optics[J]. Journal of the Optical Society of America, 2011, 28(12): 2540.

[33] BRADY D J, GEHM M E, STACK R A, et al. Multiscale Gigapixel Photography[J]. Nature, 2012, 486(7403): 386-389.

[34] BEN-EZRA M, ZOMET A, NAYAR S K. Video Super-resolution Using Controlled Subpixel Detector Shifts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(6): 977-987.

[35] ZHOU C Y, NAYAR S K. Computational Cameras: Convergence of Optics and Processing[J]. IEEE Transactions on Image Processing, 2011, 20(12): 3322-3340.

[36] JONNA S, SATAPATHY S, SAHAY R R. Super-resolution Image De-fencing Using a Nonlocal Nonconvex Prior[J]. Applied Optics, 2018, 57(2): 322-333.

[37] WANG Y L, LIU F, ZHANG K B, et al. LFNet: A Novel Bidirectional Recurrent Convolutional Neural Network for Light-field Image Super-resolution[J]. IEEE Transactions on Image Processing, 2018, 27(9): 4274-4286.

[38] ZHANG Y B, ZHANG Y L, ZHANG J, et al. CCR: Clustering and Collaborative Representation for Fast Single Image Super-resolution[J]. IEEE Transactions on Multimedia, 2016, 18(3): 405-417.

[39] EDGERTON H E. Electronic Flash, Strobe[M]. 3rd ed. Cambridge, MA, USA: The MIT Press, 1987.

[40] YOSHIDA Y, KOTANI T, NISHINO N. Electronic Camera with Repeating Flash: US7064788[P]. 2006-06-20.

[41] VEERARAGHAVAN A, REDDY D, RASKAR R. Coded Strobing Photography: Compressive Sensing of High Speed Periodic Videos[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(4): 671-686.

[42] LI X, SUN Y. Joint Structural Similarity and Entropy Estimation for Coded-exposure Image Restoration[J]. Multimedia Tools and Applications, 2018, 77(22): 29811-29828.

[43] JEON H G, LEE J Y, HAN Y, et al. Multi-image Deblurring Using Complementary Sets of Fluttering Patterns[J]. IEEE Transactions on Image Processing, 2017, 26(5): 2311-2326.

[44] LI X, SUN Y. Coded-exposure Camera and Its Circuits Design[J]. Cluster Computing, 2017, 20(4): 3003-3014.

[45] WANG Jian, XUE Tianfan, BARRON J T, et al. Stereoscopic Dark Flash for Low-light Photography[EB/OL]. [2019-05-06]. https://arxiv.org/pdf/1901.01370v1.pdf.

[46] RASKAR R, AGRAWAL A, TUMBIN J. Coded Exposure Photography: Motion Deblurring Using Fluttered Shutter[J]. ACM Transactions on Graphics, 2006, 25(3): 795-804. DOI:10.1145/1141911.1141957.

[47] DONATSCH D, BIGDELI S A, ROBERT P, et al. Hand-held 3D Light Field Photography and Applications[J]. The Visual Computer, 2014, 30(6/7/8): 897-907.

[48] PIPER J. Three-dimensional Highly Magnifying Macroscopic Light Field Photography: Theoretical Considerations and Practical Implications[J]. Journal of Advanced Microscopy Research, 2016, 11(2): 81-90.

[49] LIANG X, CHEN P, LIU B, et al. A Digital Refocusing Algorithm Based on Light Field Photography[J]. Nuclear Electronics & Detection Technology, 2015, 35(5): 434-438.

[50] CONTI C, SOARES L D, NUNES P, et al. Light Field Image Compression[M]. Springer International Publishing AG, 2019.

[51] LEVOY M, NG R, ADAMS A, et al. Light Field Microscopy[J]. ACM Transactions on Graphics, 2006, 25(3): 924-934.

[52] KAYANI S, HUSSAIN M, AHMAD M, et al. Scanning Electron Microscopy (SEM) and Light Microscopy (LM)-based Palyno-morphological Views of Solanaceae in Western Himalaya[J]. Microscopy Research and Technique, 2019, 82(2): 63-74.

[53] LIANG C K, LIN T H, WANG B Y, et al. Programmable Aperture Photography: Multiplexed Light Field Acquisition[J]. ACM Transactions on Graphics, 2008, 27(3): 1-10.

[54] INAGAKI Y, KOBAYASHI Y, TAKAHASHI K, et al. Learning to Capture Light Fields through a Coded Aperture Camera[M]//Computer Vision – ECCV 2018. Cham: Springer International Publishing, 2018: 431-448. DOI:10.1007/978- 3-030-01234-2_26.

[55] VEERARAGHAVAN A, RASKAR R, AGRAWAL A, et al. Dappled Photography: Mask Enhanced Cameras for Heterodyned Light Fields and Coded Aperture Refocusing[EB/OL]. [2019-05-09]. https://www.researchgate.net/ publication/215457338_Dappled_Photography_Mask_Enhanced_Cameras_for_Heterodyned_Light_Fields_and_Coded_Aperture_Refocusing.

[56] HAIM H, ELMALEM S, GIRYES R, et al. Depth Estimation from a Single Image Using Deep Learned Phase Coded Mask[J]. IEEE Transactions on Computational Imaging, 2018, 4(3): 298-310.

[57] CHEN P W, FANNJIANG A. Coded Aperture Ptychography: Uniqueness and Reconstruction[J]. Inverse Problems, 2018, 34(2): 025003.

[58] LUMSDAINE A, GEORGIEV T. The Focused Plenoptic Camera[C]//2009 IEEE International Conference on Computational Photography (ICCP). New York: IEEE, 2009.

[59] GEORGIEV T. Superresolution with the Focused Plenoptic Camera[J]. Proceedings of SPIE - The International Society for Optical Engineering, 2012, 7873(15): 78730X. DOI:10.1117/12.872666.

[60] LUMSDAINE A, LIN L, WILLCOCK J, et al. Fourier Analysis of the Focused Plenoptic Camera [C]//Proceedings of SPIE Multimedia Content and Mobile Devices. San Francisco, USA: SPIE, 2013, 86671M: 1-12. DOI:10.1117/12.2005781.

[61] SARDEMANN H, MAAS H G. On the Accuracy Potential of Focused Plenoptic Camera Range Determination in Long Distance Operation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 114: 1-9.

[62] MOHAN A, RASKAR R, TUMBLIN J. Agile Spectrum Imaging: Programmable Wavelength Modulation for Cameras and Projectors[J]. Computer Graphics Forum, 2008, 27(2): 709-717.

[63] USALA J D, MAAG A, NELIS T, et al. Compressed Sensing Spectral Imaging for Plasma Optical Emission Spectroscopy[J]. Journal of Analytical Atomic Spectrometry, 2016, 31(11): 2198-2206.

[64] QIAN Lulu, LYU Qunbo, HUANG Min, et al. Piecewise Spectrally Band-pass for Compressive Coded Aperture Spectral Imaging[J]. Chinese Physics B, 2015, 24(8): 080703.

[65] LI Rui, FU Longsheng. Nondestructive Measurement of Firmness and Sugar Content of Blueberries Based on Hyperspectral Imaging[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33: 362-366. DOI:10.11975/j.issn. 1002-6819.2017.z1.054.

[66] CAO X, DU H, TONG X, et al. A Prism-mask System for Multispectral Video Acquisition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2423-2435.

[67] CAO X, TONG X, DAI Q H, et al. High Resolution Multispectral Video Capture with a Hybrid Camera System[C]//CVPR 2011. New York: IEEE, 2011.

[68] LIN S S, TONG X, CAO X. High Resolution Multispectral Image Capture: US9992457[P]. 2018-06-05.

[69] LIN Y G, ZHENG Y R, FU Y, et al. Hyperspectral Image Super-resolution under Misaligned Hybrid Camera System[J]. IET Image Processing, 2018, 12(10): 1824-1831.

[70] WAGADARIKAR A, JOHN R, WILLETT R, et al. Single Disperser Design for Compressive, Single-snapshot Spectral Imaging[J]. Proc. SPIE 6714, Adaptive Coded Aperture Imaging and Non-imaging Sensors, 67140A (6 November 2007); DOI:10.1117/12.734058

Computationa l Imaging — Design for Acquisition of Plenoptic Visual Information

ZHAO Jufeng*1,2CUI Guangmang1,2

（1 Zhejiang Provincial Key Lab of Equipment Electronics, Hangzhou Dianzi University, Hangzhou 310018, China）（2 School of Electronics and Information, Hangzhou Dianzi University, Hangzhou 310018, China）

Visual light information in the real world is a complex, high-dimensional and continuous signal. However the existing digital imaging method is low-dimensional coupled discrete acquisition, which has reached the bottleneck in every dimension of imaging, such as spatial resolution, temporal resolution, visual angle and depth, color (spectrum), thus greatly limiting the full range of scene visual information. Computational imaging, which integrates multi-disciplinary knowledge in cluding signal processing, optics, vision, graphics and so on, can break through the limitations of classical imaging model and camera hardware to capture real world visual information more comprehensively and accurately. In this paper, the related concepts and theories of computational imaging are elaborated from the aspects of evolutionary history, basic principles, research trends, key technologies and future prospects.

computational imaging; plenoptic function; high dimension; computational reconfiguration

TP701

A

1009-8518(2019)05-0001-14

赵巨峰,崔光茫.计算成像——全光视觉信息的设计获取[J]. 航天返回与遥感, 2019, 40(5): 1-14.

ZHAO Jufeng, CUI Guangmang. Computational Imaging—Design for Acquisition of Plenoptic Visual Information[J]. Spacecraft Recovery & Remote Sensing, 2019, 40(5): 1-14. [DOI: 10.3969/j.issn.1009-8518.2019.05.001]

赵巨峰，男，1985年生，2013年6月毕业于浙江大学光电信息工程专业，获工学博士学位，副教授。研究方向为计算成像与图像处理。E-mail：dabaozjf@hdu.edu.cn。

2019-04-29

（编辑：毛建杰）