一种调焦机构运动方向与光轴平行性测试方法
魏鑫 何鸿涛 王建永 穆生博
一种调焦机构运动方向与光轴平行性测试方法
魏鑫 何鸿涛 王建永 穆生博
(北京空间机电研究所,北京 100094)
调焦机构运动方向与光轴平行性的好坏直接影响调焦过程中光学系统主点位置、像质均匀性、像面照度均匀性等多项指标。为了在安装过程中保证调焦机构运动方向与光轴平行,需要测量调焦机构运动方向与光轴之间的角度关系。文章通过三坐标测量系统和自准直经纬仪,设计了一种对感光元件非接触式的测量方法,来测量调焦机构运行方向与焦平面法线方向之间的角度关系,通过结构设计与加工补偿实现两者的平行装调。试验结果表明,调焦机构运动方向与焦平面法线方向的角度测量模型准确可靠,数据处理算法合理可行。
调焦机构 相机光轴 非接触式测量 平行装调 测试方法 航天遥感
0 引言
空间遥感相机是用于获取目标信息的设备,其核心是精密光学系统。在微重力、真空环境、温度交变、物距变化等工作条件影响下,光学系统的像面位置会产生变化,因此需要配备调焦机构进行焦面补偿[1-2]。
在成像跟踪领域,成像跟瞄系统用于机动目标的快速捕获、跟踪及瞄准,并对跟踪到的目标进行成像,识别目标特征[3-5]。其中,作为其重要组成部分的成像相机主要用于对捕获到的不同距离处、不同光照条件下目标的高分辨率成像。目标与设备的距离发生变化,会引起像面位置也发生变化,进而造成目标像点离焦,导致像点弥散。为了获得清晰的探测图像,需要设置调焦机构,然后根据目标到相机的距离信息调整目标像面的位置,使目标的像始终位于焦面上,从而在跟瞄时在靶面上获得清晰的图像,提高信号提取能力及测量精度,改善跟踪测量性能。对于跟踪成像系统,为了使像的信息能够准确描述空间物体的位置,相机本身必须是准确和稳定的,因此,在使用前需要对相机进行内方位元素标定,以检查在调焦过程中内方位元素的稳定性[6-7]。
调焦机构的性能主要由光学系统形式、调焦精度及使用环境条件等因素决定,常用的调焦方式有:透镜组移动式调焦、反射镜移动式调焦及焦面移动式调焦。研究表明,采用焦面移动式调焦方式对相机内方位元素的影响最小[8]。这种调焦方式要求调焦机构运动方向必须与光轴即焦平面法线方向保持一致,若调焦机构运动方向与光轴不一致,影响调焦过程中光学系统主点位置、像质均匀性、像面照度均匀性等多项指标。为了保证调焦机构运动方向与光轴平行,导轨运行方向需与探测器感光面法线方向保持一致。因此,需要在安装过程中测试调焦机构导轨运行方向与探测器感光面法线的角度关系,通过多种措施保证二者平行[9-11]。某型号光电跟瞄系统成像相机采用同轴光学系统,焦面为CMOS探测器,焦面结构简单,质量轻,因此采用沿光轴移动焦平面的方式进行调焦。本文针对该相机调焦机构,通过三坐标测量系统和自准直经纬仪,设计了一种对感光元件非接触式的测量方法,避免了接触式测量方法可能对焦平面造成的伤害,能够精确测量调焦机构运行方向与焦平面法线方向之间的角度关系,通过结构设计与加工补偿,实现两者的平行装调。该方法对采用焦面移动式调焦方式空间相机的高精度装调具有一定的借鉴意义。
1 调焦机构设计
空间相机调焦机构有多种结构型式,本文调焦机构采用凸轮滑块驱动焦平面的结构。该机构主要由步进电机、齿凸轮、凸轮轴、调焦机构座、焦面组件、焦平面、轴承、直线导轨组成,机构简图如图1所示。图1中为光轴方向,与焦平面法线方向重合,为焦平面面内两个正交方向。电机的旋转运动通过齿凸轮转化为直线运动,带动导轨沿轴运动。焦平面通过焦面组件固定在调焦机构座上,调焦机构座安装在导轨上,借助导轨沿光轴方向移动,实现调焦运动。

图1 焦面调焦机构简图
光学系统装调完成后,焦平面法线方向与光轴平行,主点位于焦平面中心位置。调焦机构带动焦平面运动过程中,相机主点位置变化主要与调焦机构的指向误差有关,如图2所示。主点在向(或向)的偏移量满足如下关系(由于向与向类似,故仅以向为例分析):
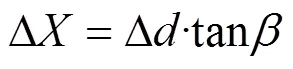
式中 β为调焦机构导轨运行方向与光轴Z之间的夹角;为导轨运行过程中主点在焦面上X方向的偏移量;为调焦机构行程。
调焦机构指向精度误差主要由两部分构成:
1)直线导轨运动直线度误差。本文中调焦机构直线导轨选用THK公司LM超精密级滚动导轨,在50mm行程内,导轨运动直线度1.5µm,像元尺寸为7µm,因此导轨运动直线度误差对主点的影响为0.2像元,满足相机主点精度小于1像元要求。
2)焦平面法线方向与调焦机构运动方向的安装平行度误差。相机装调过程中,焦平面法线方向与光学系统主光线是一致的。理想状态下,为了方便使用,调焦机构的运动方向也与相机主光线的方向保持一致。因此,焦面与调焦机构安装时,焦平面法线与调焦机构运动方向必须保持平行。本文中成像相机焦面采用CMOS探测器,焦平面通过管脚焊接在电路板上,电路板通过螺钉与焦面结构框连接。探测器安装过程中,不管是CMOS焦面与电路板的平行度关系,还是电路板自身平面度均无法得到较好的保证。可行的办法是在焦平面安装好后测量焦平面法线与调焦机构运动方向的角度,通过优化结构参数来调整两个方向的一致性。
测量平面法线方向可以通过三坐标检测或者经纬仪。测试的相机焦平面表面为蓝宝石保护玻璃,表面镀减反膜,由于三坐标探头可能伤害到镀膜表面,只能采用非接触式测量,用经纬仪自准直检测方法来实现测量。导轨运行方向不能直接测量到,可以通过三坐标测量导轨运动过程中多个状态的位置信息,拟合出导轨运动方向向量,最后通过经纬仪与三坐标测量系统间坐标系转换关系,得到焦平面法线方向与导轨运动方向的角度差异,通过结构加工补偿,实现两者的平行装调。
2 测量系统数学模型
2.1 导轨运动方向测量


式中 向量的三个分量分别为导轨运行方向向量与立方棱镜坐标系三个坐标轴X,Y,Z的夹角,通过三坐标测量系统直接输出。
2.2 焦平面法线测量方法
以经纬仪的(0°,90°),(270°,90°)方向分别为和轴建立右手正交坐标系,称为测量坐标系,记为–。假设经纬仪自准空间某单位向量,其水平角和竖直角分别为和,如图4所示,的空间向量在测量坐标系–中可表示为[14-19]

测量过程中,通常需要用到多台经纬仪,每台经纬仪确定一个自身坐标系。为了使经纬仪之间坐标统一需要经纬仪之间对瞄。因此需要在测量前确定一个基准经纬仪,其他所用到的经纬仪直接或间接地与基准经纬仪对瞄,通过对瞄数据将所有经纬仪统一到基准测量坐标系下。由于经纬仪的竖直角都是相对于大地垂直,因此,竖直角不用换算。如图5所示,假设T1为基准经纬仪,经纬仪T1与T2对瞄时两台经纬仪水平角读数分别为12和21,即经纬仪T1瞄经纬仪T2时,经纬仪T1水平角读数为12,反之经纬仪T2的水平角读数为21,T2测量向量的水平角读数为2p,那么,向量换算到经纬仪T1坐标系下的水平角读数1为


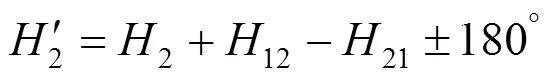
以经纬仪T1为基准坐标系利用式(3)和(1,1),以及c面法向量在经纬仪T1坐标系下的水平角和竖直角读数(2,2),可以得到立方镜坐标系的轴正方向和轴单位向量在T1–坐标系下的方向向量t和t(如式(6)、(7)所示)。则立方镜坐标系c–的轴方向的单位向量在T1–坐标系下的方向向量t可以用右手法则叉乘求得(结果见式(8))。

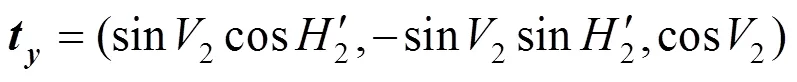

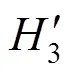

然后,再通过式(3),即可求得焦平面法线在基准经纬仪T1坐标系下的方向向量
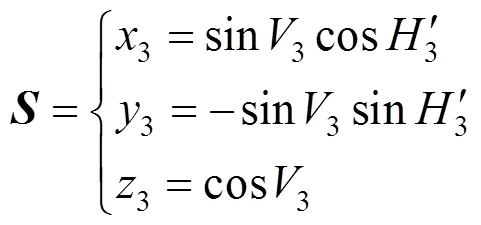
2.3 立方镜坐标系与经纬仪坐标系转换
通过经纬仪自准直测得焦平面法线在基准经纬仪T1坐标系T1–下的方向向量;同时根据经纬仪自准直测量立方镜两个镜面法线方向,求得立方镜坐标系三个方向轴在基准测量坐标系T1–下的方向向量。为了计算出焦平面法线方向与调焦机构运动方向之间的角度关系,需要将调焦机构运行方向向量与焦平面法线方向向量统一到一个坐标系下。由式(6)~(8)可以得到立方镜坐标系与经纬仪基准坐标系的转换矩阵,即

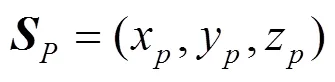
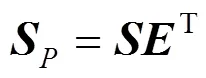


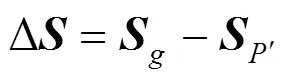
通过结构修磨调整和平移旋转,可将焦平面法线方向与导轨运动方向调整至平行。
3 试验验证
为了验证测量系统的准确性及精度,同时调整焦平面法线与调焦机构导轨方向一致,采用前文测量方法对某调焦机构组件进行了测量,并对其结构进行了调整。
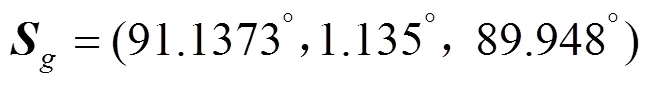
采用三台精度为1″的徕卡T3000型号经纬仪对立方镜及焦平面进行测量及对瞄,得到在基准经纬仪坐标系下,立方镜两个镜面法线及焦平面法线的经纬仪读数:


焦面组件方向安装跨距100mm,方向安装跨距60mm。根据式(1)可得,焦面组件在方向调整1.43mm,在方向调整0.47mm,在方向调整1.08mm。
调焦机构调整完成后,在实验室通过平行光管模拟不同物距,利用小孔靶标测试焦面调焦行程范围内各个位置的中心视场坐标,通过图像光斑质心算法[20]计算出调焦机构处在不同位置时相机主点位置。结果如表1所示。
表1 某相机调焦机构行程范围内主点变化

Tab.1 The principal point changes in the operation travel of the focusing mechanism
从表1可以看出,在调焦机构整个行程范围内,相机主点变化小于1个像元,精度满足要求。因此,本文测试方法合理、可行,测量结果准确、可靠。
4 结束语
本文采用非接触式测量方法,用经纬仪测量焦平面法线方向,避免了接触式测量方法可能造成的对焦平面的伤害。采用三坐标测量运动目标的运动方向,利用立方镜巧妙地将两个测量系统统一到同一测量坐标系下,实现了焦平面法线方向与导轨运动方向互相平行装调。本文讨论的测试方法,可以应用在对调焦过程中主点精度要求较高的测绘相机系统、光电跟瞄系统等相机中。
[1] 李朝辉, 王智, 乔克, 等. 三线阵立体测绘相机高精度调焦技术及实现[J]. 光学精密工程, 2009, 36(10): 41-46. LI Zhaohui, WANG Zhi, QIAO Ke, et al. Focusing Technique for Three-line Stereo Mapping Camera and Realization[J]. Optics and Precision Engineering, 2009, 36(10): 41-46. (in Chinese)
[2] 张滋黎, 邾继贵, 耿娜, 等. 双经纬仪三维坐标测量系统设计[J]. 传感技术学报, 2010, 23(5): 660-664. ZHANG Zili, ZHU Jigui, GENG Na. The Design of Double-theodolite 3D Coordinate Measurement System[J]. Chinese Journal of Sensors and Actuators, 2010, 23(5): 660-664. (in Chinese)
[3] 王建永, 张晨阳, 赵文峰, 等. 正交度对高精度二维转台测量精度的影响[J]. 航天返回与遥感, 2017, 38(3): 94-101. WANG Jianyong, ZHANG Chenyang, ZHAO Wenfeng, et al. Effects of Orthogonality on the Measurement Precision of High-accuracy Two-dimensional Turntable[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(3): 94-101. (in Chinese)
[4] 聂光戍, 刘敏, 聂宜伟, 等. 机载激光武器跟踪瞄准精度、误差源及控制分析[J]. 电光与控制, 2014, 21(1): 73-77. NIE Guangshu, LIU Min, NIE Yiwei, et al. Accuracy, Error Sources and Control of Tracking and Pointing of Airborne Laser Weapons[J]. Electronics Optics & Control, 2014, 21(1):73-77. (in Chinese)
[5] 倪茂林, 吴宏鑫. 线性不确定系统的鲁棒稳定控制器设计[J]. 自动化学报, 1992, 18(5): 585-589. NI Maolin, WU Hongxin. The Design of a Robust Stabilizing Controllers for Uncertain Systems[J]. Acta Automatica Sinica, 1992, 18(5): 585-589. (in Chinese)
[6] 邵明东, 郭疆, 孙继明. 离轴三反测绘相机调焦机构的设计[J]. 中国光学, 2012, 5(4): 373-378. SHAO Mingdong, GUO Jiang, SUN Jiming. Design of Focusing Mechanism for off-axis TMA Mapping Cameras[J]. Chinese Optics, 2012, 5(4): 373-378. (in Chinese)
[7] 占潜, 高云国, 于萍. 光电探测器调焦机构的设计与精度分析[J].激光与红外, 2014, 44(11): 1238-1243. ZHAN Qian, GAO Yunguo, YU Ping. Design and Analysis on Focusing Mechanism of Photoelectric Detector and Its Precision[J]. Laser&Infrared, 2014, 44(11): 1238-1243. (in Chinese)
[8] 邵明东, 郭疆, 朱磊, 等. 调焦方式对测绘相机主点位置的影响[J]. 中国光学, 2013, 6(5): 773-779. SHAO Mingdong, GUO Jiang, ZHU Lei. Effects of Focusing Method on Principal Point of Aerospace Mapping Camera[J]. Chinese Optics, 2013, 6(5): 773-779. (in Chinese)
[9] 岳丽清, 张继友, 付瑞敏, 等. 三线阵相机视轴夹角及线阵平行性装调测试[J]. 航天返回与遥感, 2012, 33(3): 35-40. YUE Liqing, ZHANG Jiyou, FU Ruimin, et al. Alignment Method of Axis Angle and Linear Array Parallelism for Three-line Array Mapping Camera[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 35-40. (in Chinese)
[10] 刘达, 钟红军, 李春江, 等. 星敏感器调焦方法研究[J]. 空间控制技术与应用, 2015, 41(1): 59-62. LIU Da, ZHONG Hongjun, LI Chunjiang, et al. Focusing Methods of Star Sensor[J].Aerospace Control and Application, 2015, 41(1): 59-62. (in Chinese)
[11] 岳春宇, 何红艳, 邢坤, 等. 多谱段光学遥感探测器配准误差分析[J]. 航天返回与遥感, 2017, 38(2): 100-108. YUE Chunyu, HE Hongyan, XING Kun, et al. Registration Error Analysis of Multispectral Optical Remote Sensing Detector[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(2): 100-108. (in Chinese)
[12] 杨再华. 航天器总装精度测量方法分析[J]. 航天器环境工程, 2007, 24(6): 390-392. YANG Zaihua. An Analysis of Measurement Technology in Spacecraft Assembly[J]. Spacecraft Environment Engineering, 2007, 24(6): 390-392. (in Chinese)
[13] 杨再华, 孙刚, 刘建新. 采用经纬仪测量航天相机视轴的方法分析[J]. 航天器环境工程, 2010, 27(1): 92-94. YANG Zaihua, SUN Gang, LIU Jianxin. Measurement of Orientations of Optic Axis of Space Camera with Theodolite[J]. Spacecraft Environment Engineering, 2010, 27(1): 92-94. (in Chinese)
[14] 杨振, 李广云, 范百兴, 等. 多种互瞄条件下立方镜准直传递方法研究[J]. 宇航计测技术, 2013, 33(6): 11-13. YANG Zhen, LI Guangyun, FAN Baixing, et al. Cubic Prism Collimation Vector Delivery Methods under Various Aiming Conditions[J]. Journal of Astronautic Metrology and Measurement, 2013, 33(6): 11-13. (in Chinese)
[15] 吴国栋, 宋丹. 测绘相机坐标系与立方镜转换矩阵的标定[J]. 光学精密工程, 2007, 15(11): 1727-1730. WU Guodong, SONG Dan. Calibration of Mapping Camera and Cubic Prism Coordinate System[J]. Optics and Precision Engineering, 2007, 15(11): 1727-1730. (in Chinese)
[16] 汪逸群, 颜昌翔, 贾平. 非接触式扫描反射镜定位精度检测方法[J]. 红外与激光工程, 2012, 41(4): 1057-1061. WANG Yiqun, YAN Changxiang, JIA Ping. Non-contact Position Precision Detecting Method of Scanning Mirror[J]. Infrared and Laser Engineering, 2012, 41(4): 1057-1061. (in Chinese)
[17] 任顺清, 陈海兵, 赵洪波. 用经纬仪测量大尺寸三维导轨垂直度的方法[J]. 仪器仪表学报, 2012, 33(1): 188-193. REN Shunqing, CHEN Haibing, ZHAO Hongbo. Perpendicularity Measurement Method of 3-D Large Guideway with Theodolite[J]. Chinese Journal of Scientific Instrument, 2012, 33(1): 188-193. (in Chinese)
[18] 邢辉, 焦文春, 王昀. 红外低温相机视轴引出方法[J]. 光学学报, 2013, 33(1): 0112008-1-0112008-7. XING Hui, JIAO Wenchun, WANG Yun. Method to Elicit the Boresight of Infrared Cryogenic Camera[J]. Acta Optica Sinica, 2013, 33(1): 0112008-1-0112008-7. (in Chinese)
[19] 吴国栋. 离轴三反时间延迟积分CCD相机内方位元素和畸变的标定[J]. 光学精密工程, 2012, 20(3): 462-467. WU Guodong. Calibration of Inner Orientation Parameters and Distortion for Three-mirror Off-axis TDICCD Camera[J]. Optics and Precision Engineering, 2012, 20(3): 462-467. (in Chinese)
[20] 樊巧云, 张广军. 离散噪声图像的光斑质心算法及其硬件实现[J]. 光学精密工程, 2011, 19(12): 2992-2998. FAN Qiaoyun, ZHANG Guangjun. Spot Centroiding Algorithm for Discrete Noise Image and Its Hardware Implementation[J]. Optics and Precision Engineering, 2011, 19(12): 2992-2998. (in Chinese)
A Measurement Method of Parallel Accuracy between the Motion Direction of the Focusing Mechanism and the Optical Axis
WEI Xin HE Hongtao WANG Jianyong MU Shengbo
(Beijing Institute of Space Mechanics & E1ectricity, Beijing 100094, China)
Parallelism between focusing-mechanism motion direction and optical axis influences the principal point position, image quality uniformity, and illumination uniformity, etc. The measurement of angular deviation between focusing-mechanism motion direction and optical axis is necessary to satisfy this parallelism parameter requirements. A non-contact measurement method by means of three-coordinate measuring machine and collimation theodolite is provided in this article, which can measure the angle between focusing-mechanism motion direction and optical axis. By structural design optimization and machining compensation, parallel alignment is realized. Testing results demonstrate that the measurement method is accurate and reliable, and the data processing is reasonable.
focusing mechanism; optical axis; non-contact measurement; parallel adjustment; measurement method; space remote sensing
V556
A
1009-8518(2019)05-0067-08
魏鑫, 何鸿涛, 王建永, 等. 一种调焦机构运动方向与光轴平行性测试方法[J]. 航天返回与遥感, 2019, 40(5): 67-74.
WEI Xin, HE Hongtao, WANG Jianyong, et al. A Measurement Method of Parallel Accuracy between the Motion Direction of the Focusing Mechanism and the Optical Axis[J]. Spacecraft Recovery & Remote Sensing, 2019, 40(5): 67-74. [DOI: 10.3969/j. issn.1009-8518.2019.05.007]
魏鑫,女,1985年生,2010年获中国空间技术研究院飞行器设计专业硕士学位,工程师。主要研究方向为空间遥感相机结构设计。E-mail:582769868@qq.com。
2019-05-05
国家重大科技专项工程
(编辑:夏淑密)

