三相逆变器双闭环控制系统仿真研究
胡维飞,张永明
(上海电机学院电气学院,上海201306)
0 引言
三相逆变器作为目前极其常见的电子设备,针对其输出端的要求也越来越高,例如当负载频繁变化时表现出较硬的输出外特性、鲁棒性好[1]。目前,对三相逆变系统控制器的研究,主流方法是采用比例积分[2-3]或者PR 控制[4]、重复控制[5]或者无差拍控制[6]等。对于直流输入信号,其中PI 可以做到无静差跟踪,且具有控制结构简单、动态响应较快以及鲁棒性好等特点,在电气工程领域得到广泛应用。比例谐振(PR)可以对某一特定频率的正弦交流信号进行跟踪。但是PR 控制在计算时需要进行离散化处理,并且PR 动态响应速度不如PI 控制。重复控制虽然可以消除幅值和相位的稳态误差,但是,利用该方法时输出周期有延迟且动态响应不佳,并且控制器的设计比较复杂。无差拍控制虽然有着良好的动态响应,且无超调现象,但是其控制特性在系统参数变化时有较大的影响,鲁棒性较差,不利于对输出电压的控制[7]。
因此,本文将采用比例积分控制方案,利用电压外环电流内环的双闭环控制策略作为三相逆变器的控制系统。本文通过详细介绍三相逆变器的数学模型,计算双闭环控制策略的传递函数,最后在MATLAB/Simulink 上搭建逆变系统的仿真模型,验证控制策略的有效性。
1 三相逆变器的数学模型
1.1 基于三相静止坐标系的数学模型
如图1 所示为三相逆变器的主电路拓扑结构,输出端采用LC 滤波电路,其中,其中r 为滤波器的等效阻抗。直流侧输入电压为udc,A、B、C 三点电压分别为UA、UB、UC,他们是相对直流输入端中点P 的三相电压,输出端电感电流分别为ila、ilb、ilc,电容电压分别为Uoa、Uob、Uoc,流入三相负载的电流分别为ioa、iob、ioc[8]。
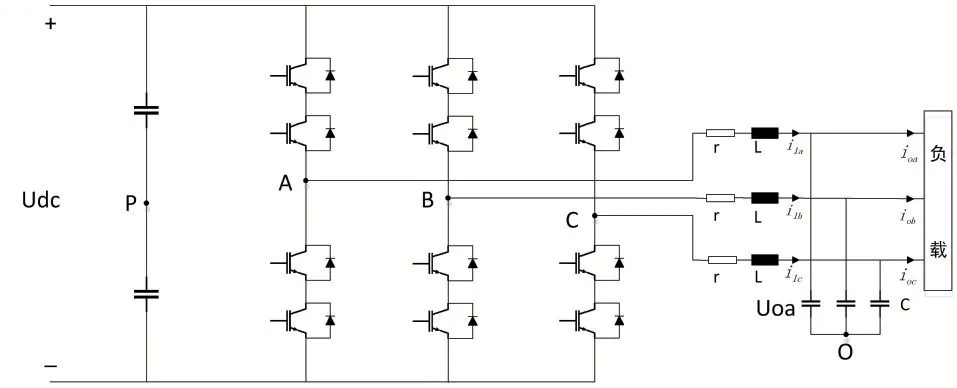
图1 三相逆变器主电路拓扑图
由KCL 和KVL 可列出下列方程:
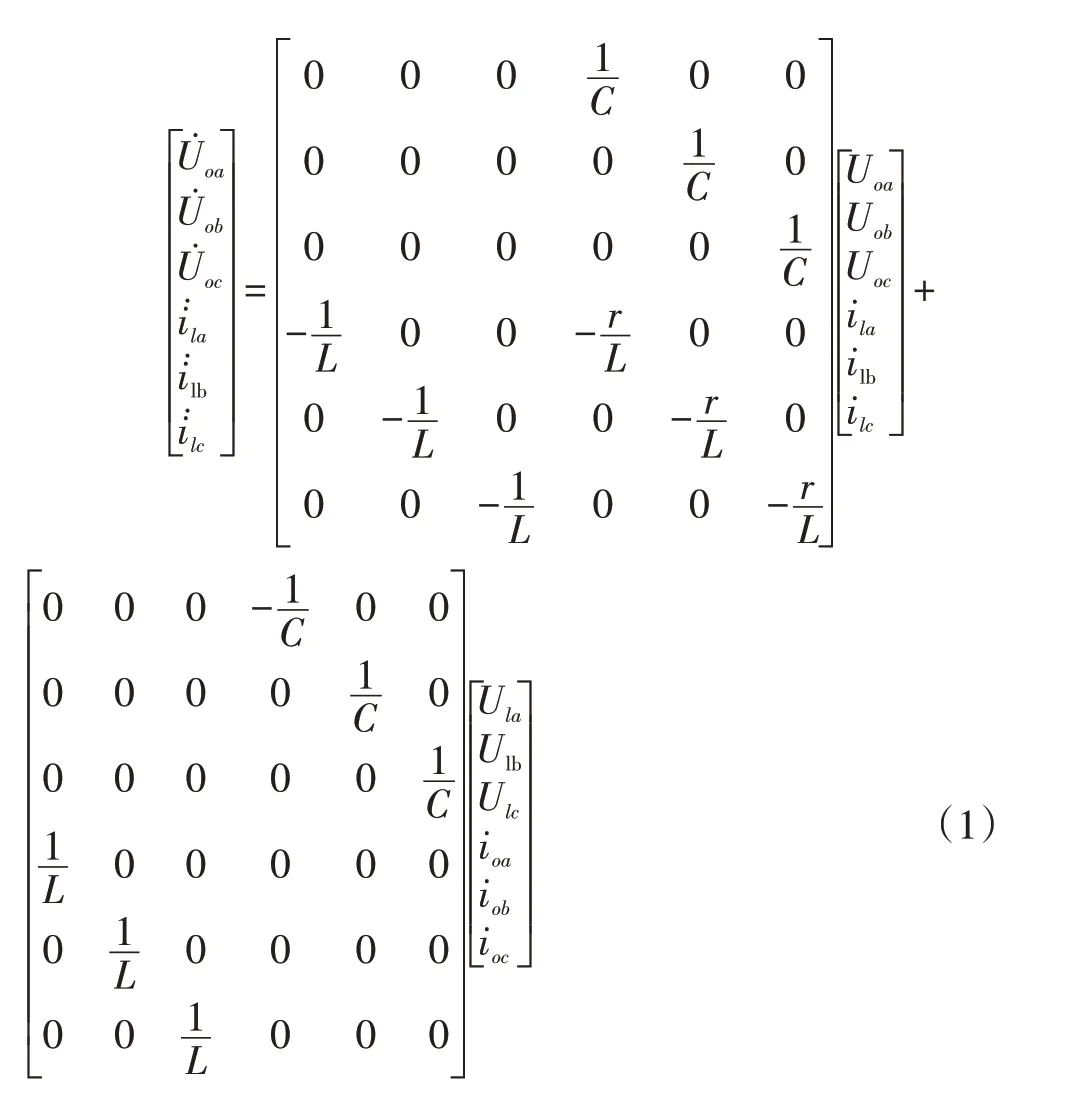
将上式化简可得:

采用电容电压和电感电流作为状态变量,可得通用连续状态空间模型为:

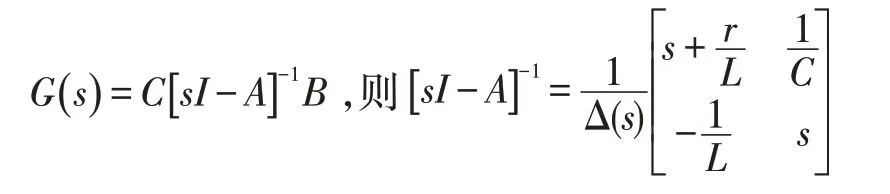
其中Δ(s)=s2+,由此可以求出输入电压同输出电压之间的传递函数为:

输入电压同输出电流之间的传递函数为:

1.2 基于d-q旋转坐标系下的数学模型
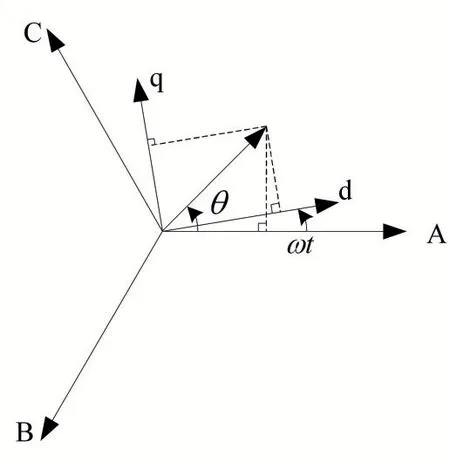
图2 坐标变换图
根据图2 中各矢量的几何关系,可以求出坐标变换后的状态空间表达式如下:


图3 旋转坐标系下逆变器数学模型
2 三相逆变器双环控制策略分析
对于三相逆变器控制系统的双闭环控制策略,电流内环控制可以增加控制系统的带宽,同时系统的瞬态响应速度更快,当系统带非线性负载时,适应能力更强,且输出电压的谐波失真情况也随之降低,提高系统输出波形的稳定性和供电质量。而电压外环控制的作用是使系统输出波形能够瞬时跟踪给定值。目前,基于大多数逆变系统中常用的双闭环控制的电流内环控制策略是以输出端的滤波电感电流为内环控制或者以滤波电容电流为内环进行控制。其中,采用滤波电容电流作为内环进行控制时,由于电容电流能够被瞬时控制,使得输出电压因为电容电流的微分环节得到矫正,因此,该系统的带负载能力更强,本文将采用电容电流为内环进行分析,如图4 所示为电容电流为内环的控制框图。

图4 电容电流内环电压外环控制框图
根据自动控制理论,可以采用极点配置法计算PI控制器的比例和积分控制参数,因为采用极点配置法时,比例和积分控制参数与闭环控制系统性能指标能建立量化关系,使得参数计算更加准确。图4 中控制器的Gv与Gi分别定义为:

由图4 可以推出逆变器的闭环系统特征方程:
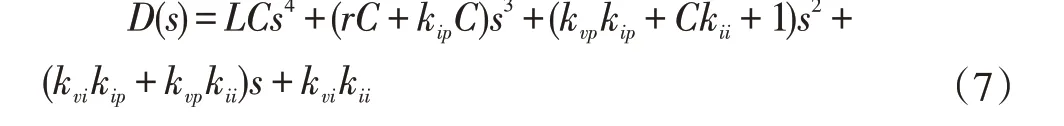
从上式可以看出此系统是一个四阶系统,特征方程有四个根也就是说有四个闭环极点。使用伯德图法、根轨迹法等一般方法设计双闭环控制器时需要考虑调节器之间的响应速度、频带宽度等多方面因素的互相影响,控制器设计步骤复杂,人工计算量大,而且还需反复凑验;使用极点配置法不仅简化设计过程还可减少人工计算量,而且所设计的参数能满足系统高性能指标要求。
则由期望的主导极点与非主导极点所得闭环方程为:
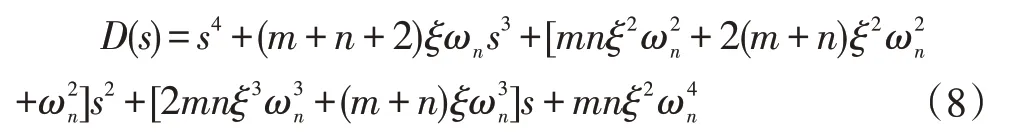
对比式(7)和式(8),令对应系数相等,可得:
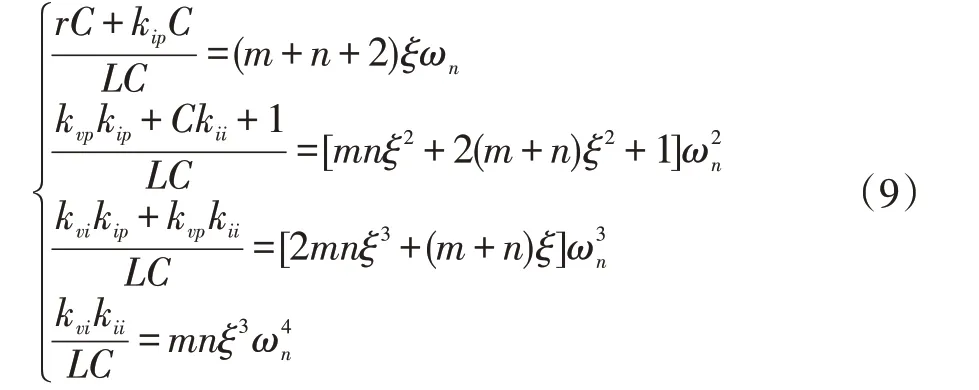
为使得计算方便,现令:
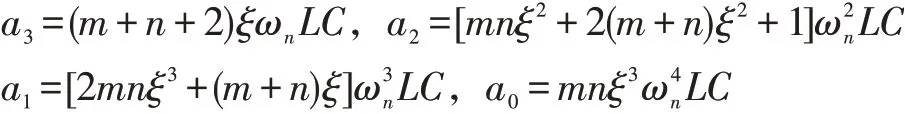
联立上式可求得:
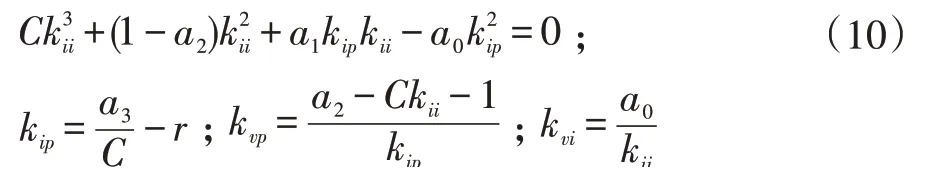
其中,根据kip的值可以求出式(10)的解,而kii即为该式的正实数根。
3 三相逆变器的仿真
根据上述分析,对三相逆变器的数学建模以及控制策略进行计算,利用MATLAB/Simulink 仿真平台搭建逆变系统的仿真模型,对三相逆变器进行仿真,验证控制策略的可行性与有效性。
3.1 滤波器参数设计
本文所设计的逆变器是通过以SVPWM 为控制信号来控制开关器件的通断将直流输入电压转换为正弦波等效的波形输出,所以输出电压中包含有较多的高次谐波。为了使逆变器带上负载后输出能得到平滑的、波形质量好的输出电压,因此必须在负载前端加低通滤波器以消除高次谐波分量,通常釆用LC 滤波器。
根据工程实践,滤波器自身电感与电容的计算公式如下:
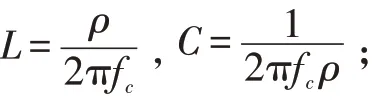
其中fc为滤波器的截止频率,一般取为逆变器开关频率的0.04-0.1 倍,ρ 为逆变器自身等效阻抗,一般取额定负载的0.4-0.8 倍。
综合考虑整个逆变器的谐波输出大小、控制算法及电感压降等因素,通过计算,选取滤波器的电感值为2mH,滤波器的电容值为6 μF。三相逆变器的阻尼比c为ξ=,谐振频率为ωn=所以,控制器参数可以计算得出:电压环控制器参数:kvp=2.64e-3,kvi=1431;电流环控制器参数:kip=5.896,kii=356.394。
3.2 Simulink仿真分析
根据前面所给的系统参数,搭建仿真模型,对三相逆变器在不同工况下进行仿真。仿真结果如下。
(1)额定负载:Ra=Rb=Rc=6Ω,仿真结果如图5所示,由波形图可以看出,所搭建的电压电流双闭环系统模型有较好的输出波形质量。

图5 闭环稳定工况时,输出电压和电流波形
(2)负载突变:在0.05s 时设置使得负载发生突变,此时Ra=Rb=Rc=3Ω,仿真结果如图6 所示,该逆变系统的输出电压电流波形在0.05s 负载发生突变时,电压电流均有轻微波动,但是在极短的时间内即可恢复稳定。
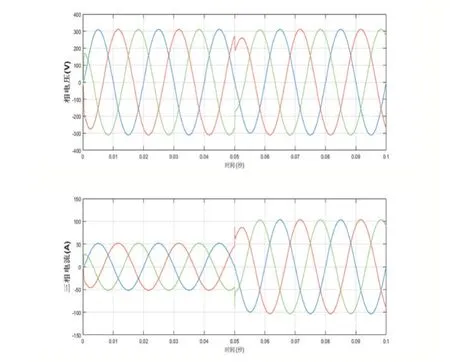
图6 闭环负载突变时,输出电压和电流波形
(3)直流电压源突变:在0.05s 时设置使得直流源发生突变,如图7 所示,其中(a)图为直流源从1500V瞬间增加到1800V 时的波形,(b)图为直流源从1500V瞬间减小到1200V 时的波形,从仿真结果来看,输出电压均能在极短的时间内回复到正常水平。

图7 闭环直流电压源突然增大和减小时,输出电压波形
经过上述波形图分析可知,采用以电容电流为内环的双闭环为控制策略之后,无论是负载发生突变或者是直流源发生突变的情况,输出波形均能在很短的时间稳定下来,说明该系统是稳定的。
4 结语
本文主要研究了三相逆变系统的闭环控制系统。着重的研究逆变器在静止和旋转坐标系下的数学模型,推导传递函数计算系统稳定性。最后在前文理论分析的基础上,基于仿真工具MATLAB/Simulink 搭建辅助逆变器系统实验平台。对文中提出的逆变器电压控制方法进行负载投切实验、直流源突变的仿真实验,结果完全符合设计要求。

