气温对树木生长影响的研究

孙小珺，孙杰，尹若波,张德全,王克华,于凌飞，张靖

(1.山东省龙口市森林病虫害防治站，山东 烟台 265701;2.龙口市国有林场，山东 烟台 265701;3.山东省林业外资与工程项目管理站，山东 济南 250014;4.山东省林业监测规划院，山东 济南 250014)

为了全面提升森林质量，增加森林碳汇量，必须探求影响树木生长的主要因子及其影响程度。张德全[1]、巩延苹[2]、张靖[3]、董兴囤[4]、杨科家[5]分别对降水量、光照、时间等因素对树木生长的影响进行了研究，赵西平[6]对温度影响的研究进展进行了论述。众所周知，树木的生长主要是以光合作用为基础，经历一系列的生理生化过程，但是所有这些过程，必须在一定气温条件下进行。笔者应用数学模拟方程对影响树木生长的因子气温进行了探讨。

1 资料来源

历年平均气温数据材料由烟台市牟平区气象局提供。解析木数据资料来源于2013年3月中旬在烟台市牟平区昆嵛山林场采集的2株赤松解析木(分别为65年生和45年生)和风云林场2株赤松解析木(分别为77年生和61年生)。树高超过10 m的，采用2 m区段法截取圆盘；树高不到10 m的，采用1 m区段法截取圆盘。对圆盘正面扫描后，用CAD程序进行影像处理和判读，分别判读各个圆盘每个年轮的树径值，由此推算各年度的树高及树木材积。

2 研究方法

树木的生长量指标，如树径、树高、材积生长量、森林生物量、森林碳储量均与年气温(及其累加值)之间表现出十分显著的相关关系，用指数经验方程y=exp(a+bx)来判断因变量y随自变量x的变化程度(变化速度)，其中y为树木的生长量指标，x为年平均气温等自然因素指标，a,b为待求系数(下同)。用混合经验方程y=exp(a-b/x)来寻求效益指标最大化，即用最少的投入(包括时间)以求获得最大的收益。笔者经过研究，通过以每一年为研究对象，对方程进行拟合试验，结果除个别指标表现出相关关系显著外，大部分指标相关关系不显著，而通过累加效应(即用累计生长量与树木年龄、日照时数累加量等建立回归相关方程)，则表现出十分显著的相关性

用数学方程y=exp(a+bT)和y=exp(a-b/T)求得树木生长量指标与年均气温(包括累加值)的回归系数，再用树木年龄的回归方程[5]计算树木生长生命力(树木生长量与时间因子的数学方程的拟合值与树木实际生长量的比值定义为时间影响力，即树木生命力)，对年均气温对树木生长的贡献率进行分析研判。

3 结果与分析

用77年生赤松解析木材料进行研究，用D1-0.5代表0.5 m高处树径项目，余者类推，用H2代表树高项目，用V1代表树木材积项目。用Y(T)代表以年均气温(及其累加值)为自变量、以树木各种指标的生长量为因变量的函数。分别利用经验方程y(T)=exp(a+bT) 和y(t)=exp(a-b/T)建立数学回归方程。计算结果详见表1、表2。由表1、表2可知，计算结果均未出现异常现象，均具有一致性，表明结果稳定可靠，试验精度达到99.99%以上，表1除D1-5.0项目外，其余项目的精度接近100%。

表1 77年生树木生长量与年均气温数学方程拟合表

表2 77年生树木生长量与年均气温数学方程拟合表

以树木生命力为因变量，以年均气温数据为自变量，重新建立数学方程进行拟合，结果见表3、表4。由于得出的混合函数方程结果精度很低，笔者不再在表中列出。从表3中可以看出，拟合结果除个别项目(D1-4.5)外，精度均接近100%，因此可以应用。从函数曲线的发展态势可以看出，由于所有研究指标的非负性，指数函数方程y=exp(a+bT)是研究y随T的增长的趋势，混合函数方程y=exp(a-b/T)是研究y随T的下降趋势，由于笔者直接用后32 a的年均气温数据资料进行的赤松生长量和年均气温之间的拟合试验，由于缺少前35 a的降水量资料，而生长量又是整个年份的累加，因此表3中的b值均为负值，翻番年均气温累加事实上也是负值，指的是下降一番(即下降50%)的年均气温累加数，改为正值就是翻番年均气温累加数。再以表3中的D1-0项目说明如何推算相对贡献率。表中折算翻番时间为34.9 a，可以理解为是扣除了树木生长曲线(S形)特性影响以后的数值，它与树木生长量与时间经验方程y=exp(a+bt)同一项目指标25.8 a的差值9.1 a，也就是树木本身生长特性比增均气温单独影响提高了3.6 a，所以该项目的相对贡献率为1÷[1+(9.1÷34.9)]=79.3%。用同样的方法计算出其他项的相对贡献率。从计算结果可以看出降水量对树木生长量影响的相对贡献率，表3数值在64.3%～78.7%之间，表3数值在50.9%～57.4%之间，数值指标变化幅度不大，表现稳定，两表之间的数值相差12%左右，可能是由于研究精度的差别所致。笔者认为表3的精度较高，可靠性大。因此年均气温对树木生长量影响权重达到74.1%，可见研究气温对树木生长量影响是何等的重要。从试验中可以看出，气温相对贡献率、光照相对贡献率与降水相对贡献率相比变化不大，从高到低依次排序为光照、气温、降水。

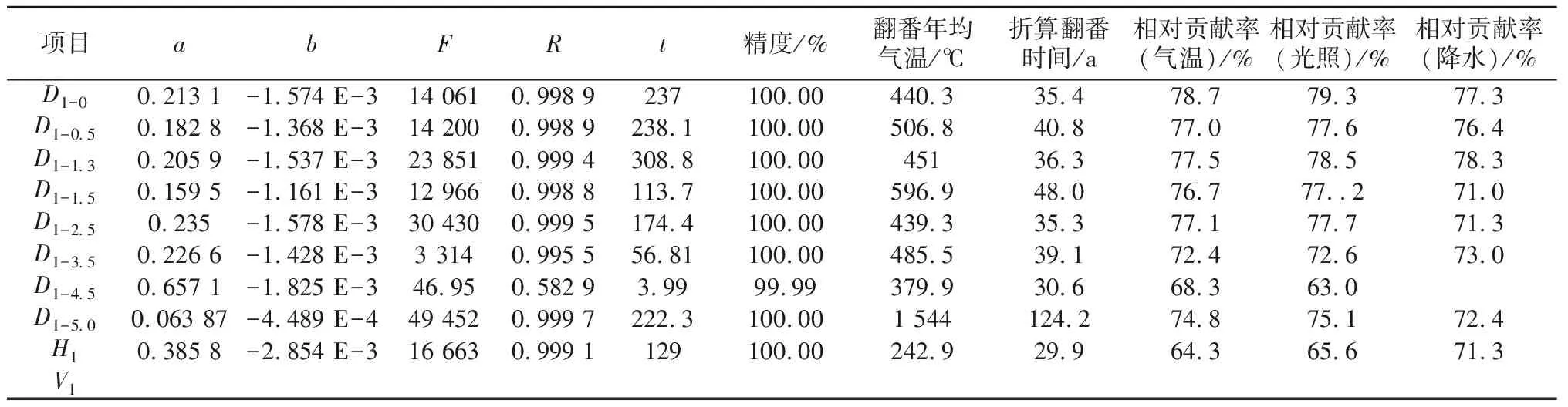
表3 77年生树木生命力与年均气温数学方程拟合表

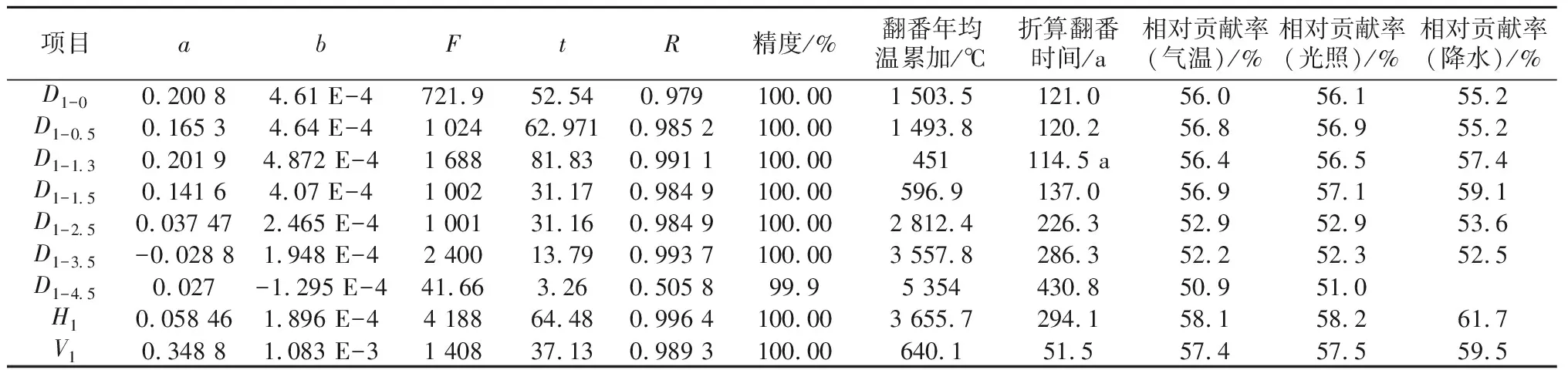
表4 77年生树木生命力与年均气温数学方程拟合表

以同样的方法对另外3株样木进行了同样的试验，取得了较好的试验效果，以此3株样木试验结果对以上的试验结果进行适合性检验。检验结果如表5所示。表中FZ-2与FZj-2分别代表树木生长量与年均气温方程、树木生长生命力与年均气温方程拟合值同2号样木比较的F值，FH-2与Fhj-2分别代表混合树木生长量与年均气温方程、树木生长生命力与年均气温方程拟合值2号样木的F值，D0代表地径项目,余者类推。

表5 经验方程适合性检验表

通过查表，F0.05-30(可靠度95%，自由度30的F值)为1.84，在表5中，凡超过这一数值的，就算未通过适应性检验，只有树木生长生命力方程拟合数据试验部分通过了检验，从中可以看出年龄相近的样木更容易通过适用性检验。因此经验方程系数不能借用，必须在条件具备的条件下重新进行方程拟合试验，直到通过适应性检验为止。从表5中也可以看出，项目FZ-1与FH-1的D0R的F值的比值为1.256，也小于1.84，这叫通过间接验证。通过分析计算，大部分均能通过直接和间接验证。

4 结语

笔者用模拟方程对树木生长量与年均气温关系系进行研究，开辟了一种崭新的途径。指数方程呈指数增长，也就是递增的意思，是树木生长上升潜力的表达式，反映出树木生长的速度问题；而另一混合方程则是树木生长下行压力的表达式，它揭示了效益最大化问题。通过对树木自身增长潜力作用的剔除，可得平均气温对于树木生长的相对贡献率，从增长潜力看，相对贡献率均值为74.1%，从增长的下行压力看，相对贡均率均值为55.3%，二者的中值为64.7%，这就是说树木的生长相对于树生长特性来说，气温对树木生长的影响起到65%左右的作用，树木本身特性仅占35%左右。