软土地层减振式地下车站结构综合研究

池君宇，马忠政，黄继成，马险峰,3

(1.同济大学 地下建筑与工程系，上海 200092；2.上海申通地铁集团有限公司，上海 200233； 3.同济大学 岩土及地下工程教育部重点实验室， 上海 200092)

近年来，中国城镇化建设发展迅速，城市人口激增，轨道交通已逐渐成为缓解城市交通压力的主要交通方式。目前，我国城市轨道交通多位于城市主干道下，形成庞大的地下网络，给城市生活带来很多便利。同时，由于地下空间开发利用率的提高，新建地铁线路离周边建筑越来越近，甚至从建筑物下穿越，使地铁运行时的环境振动问题更加突显[1-5]。

现如今国内外进行了关于地铁运营产生的振动、噪声等问题的相关研究。英国铁路管理局做了实验监测研究，研究了轨道相关参数和地铁车辆的车速与激振频率之间的相关性以及共振等问题。Krylov等[6]将高速轨道简化成Euler-bernoulli梁，研究了列车振动的影响。英国剑桥大学的Hunt[7]运用随机振动的理论方法，研究路面不平对地面振动的规律。德国Melke[8]提出了一种诊断环境振动的新方法，并用该方法预测了城市铁路附近的建筑物水平振动，根据得到的数据整理分析，总结了振动波的传播规律。Gardien等[9]分析了Netherlands的地铁振动的传播规律，研究了不同模型参数对计算结果的影响。国内白冰等[10]采用二维数值模型计算方法对地铁振动作用下隧道的结构动力响应。研究表明振动导致隧道内力值得到大幅提高。张玉娥等[11]、刘建达等[12]、王祥秋等[13]采用二维有限元模型研究了隧道断面形式、埋深、平行隧道净距、地质条件等对振动的传播和衰减规律的影响。黎泳言等[14]用ANSYS，通过建立排水沟-路面-土三维模型，模拟分析排水沟深度、宽度以及沟内水位、沟壁填充对隔振效果的影响。Li等[15]对上海高速磁浮进行分析，测试了高速磁浮列车线路周边环境；研究了地面振动衰减规律以及不同列车速度和轨道结构在时域和频域内参数的振动影响。总的来说，目前关于地铁引起的振动波的传播规律和造成的环境影响研究大都采用现场实测和经验公式。这些方法由于各个工程存在轨道系统和环境条件的差异，不能普遍应用于其它工程。

上海的地铁网络密集，对一些特殊建筑物如精密实验室等会产生影响，需要对车站结构减振隔振进行研究。

1 工程实例

1.1 工程概况

上海轨道交通十号线二期工程国帆路站是12.5 m站台地下三层岛式车站，主体结构尺寸155.00 m×20.04 m(内净距)，是一座地下车站，车站的位置是杨浦区淞沪路下，沿淞沪路方向布置，呈南—北走向。由于规划选址的限制，该站北边挨着国帆路，东面是合生江湾国际公寓，西边则是复旦大学江湾校区。复旦大学校区里有一座先材楼，是国家重点物理实验室，对环境振动十分敏感。

1.2 周边环境条件

图1为国帆路站周边环境条件，图中复旦大学先材楼为7层框架结构，桩基础，距离车站主体基坑约43.58 m，距3号出入口约33.64 m；合生江湾国际公寓为16层房屋，一层地下室，采用桩基础，围护为双头搅拌桩，桩长10.80 m，距车站主体基坑约25.08 m，距1号风亭及出入口约17.85 m，距2号风亭及出入口约29.00 m。

车站共设3个出入口和2组风井，其中西侧靠近复旦大学处仅设1座出入口，其余2座出入口及风井均设于远离学校的车站东侧。

图1 国帆路周边环境示意图

1.3 工程地质条件

拟建场地处于古河道分布区，为第四纪上更新世Q3至全新世Q4沉积物，大部分组成为饱和黏性土、粉性土及砂土，具有成层分布的特点。

1.4 水文地质条件

拟建场地浅部土层中的地下水类型为潜水。潜水稳定水位埋深为0.50 m～2.60 m(绝对标高为1.80 m～3.84 m)，平均埋深为1.27 m(平均标高为2.95 m)。

2 车站不同结构型式减振效果数值模拟

2.1 结构选型的思路和方法

研究方法采用数值仿真计算，通过现场实测上海地铁运营产生的轨道竖向加速度，把它当作激励施加在车站模型上，然后监测距离车站一定水平距离地表点的加速度时程图，通过加速度时程图的比较可以得出叠合墙式、复合墙式、离壁墙式三种结构方案在结构减振方面利弊。

地铁引起的振动传播是波动的传播问题。当施加较单一频谱的激励体系在弹性范围内，采用频域的波动分析求解是可行的。对于地铁振动的情况，复杂的土壤分层，加上宽频谱的振动激励，不宜采用频域计算。结构体系进行动力分析时，时域分析与频域分析本质上是一致的，可以采用时域有限元模拟地铁振动。

2.2 地铁车站三种结构方案

(1)叠合墙式方案。内墙和外墙完全连接，内外墙间可传递法向力、剪力和弯矩。方案剖面图如图2所示。

(2)复合墙式方案。内墙和外墙之间有一定分离，可传递法向力。方案剖面图如图3所示。

图2 叠合墙剖面图

图3 复合墙剖面图

(3)离壁墙式方案。内墙和外墙分离，中间有1 000 mm间隙，留下的混凝土支撑传递法向轴力。方案剖面图如图4所示。

图4 离壁墙剖面图

三种结构方案在有限元软件ABAQUS中的实现方法如表1所示。

表1 三种结构方案实现方法

2.3 建立数值计算模型

截取地铁车站典型的一段(8 m)对地铁车站建立有限元模型进行计算分析，建立准三维有限元模型，并且约束模型轴向自由度来模拟仿真。

由于结构和土体的相互作用，建模时水平方向土体尺寸按关注的区域范围取，即离车站结构外墙100 m，竖直方向按车站结构竖向尺寸的3倍来选取，即离地面75 m。设置人工边界，减少波在边界上反射影响。由于结构对称，取半结构计算 。建立有限元模型如图5、图6所示。

图5 车站-土体三维有限元模型

图6 车站局部放大的有限元模型

2.4 数值计算

输入荷载为上海某一相同车型地铁车站列车通过时实测的床加速度时程记录，记录分别距离外墙0 m、50 m、100 m的控制点1、2、3三个点的数值计算结果。将复合墙式结构、叠合墙式结构和离壁式结构这三种结构在控制点1、2、3处的频谱图记录如图7—图9所示。图中DHQ代表叠合墙、FHQ代表复合墙、LBQ代表离壁墙。

图7 控制点1处三种结构的频谱图

图8 控制点2处三种结构的频谱图

图9 控制点3处三种结构的频谱图

将复合式结构、叠合式结构和离壁墙式结构三种结构地表加速度峰值衰减曲线和Z振级衰减曲线如图10—图11所示。

考虑到上海市常见的车站型式为叠合墙式，为了清楚的显示三种结构型式抗振的不同，以叠合墙式车站对应振动作为参考标准，按下式定义减振效果系数d：

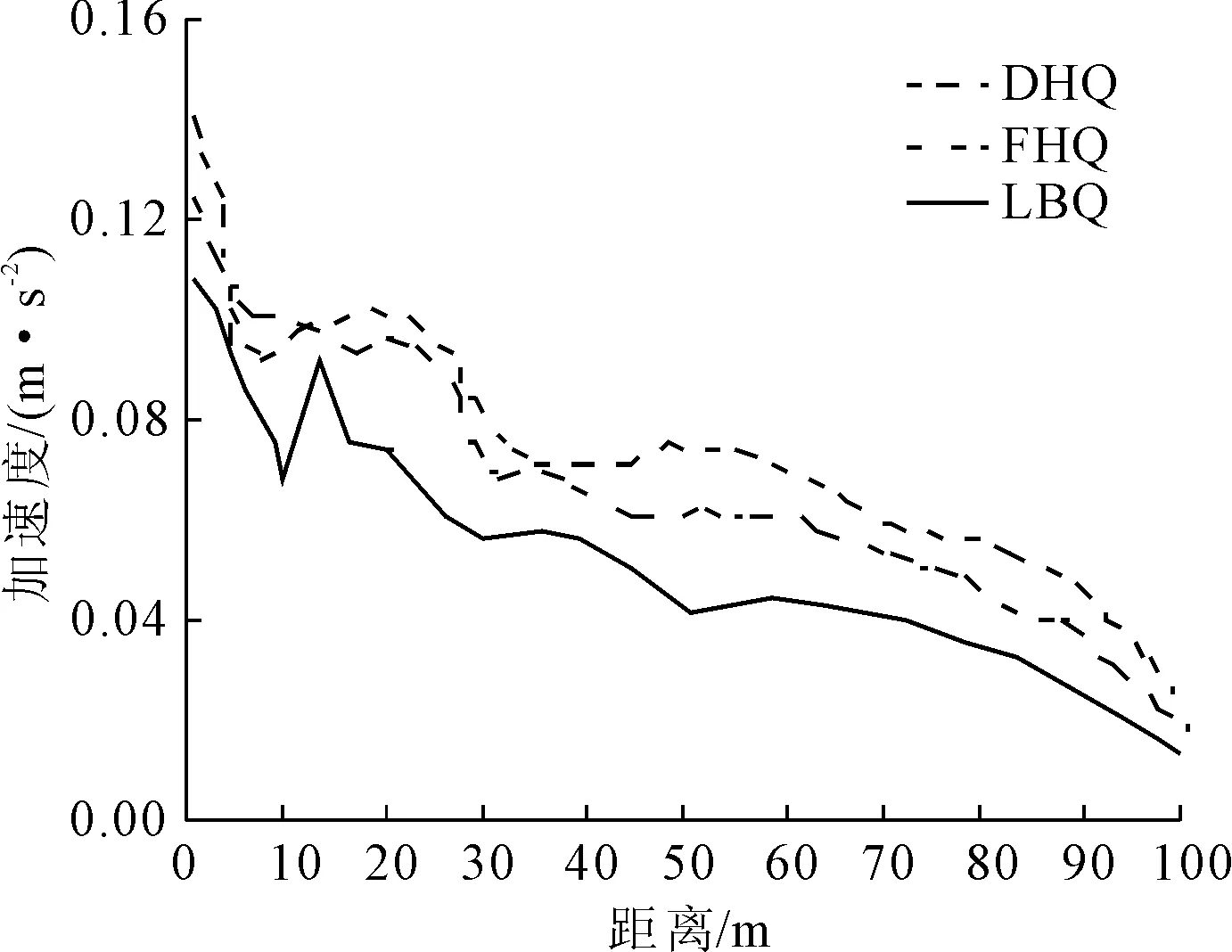
图10 地表加速度峰值衰减曲线

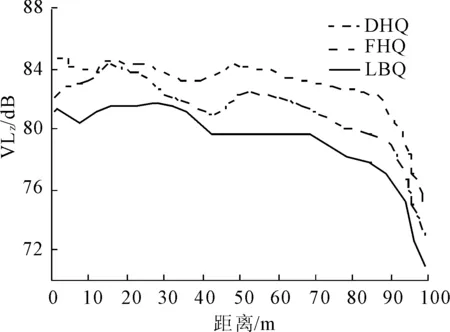
图11 地表Z振级衰减曲线

式中：aw0为叠合墙式方案振动计权加速度有效值，aw为振动计权加速度有效值。

将计算结果列于表2。

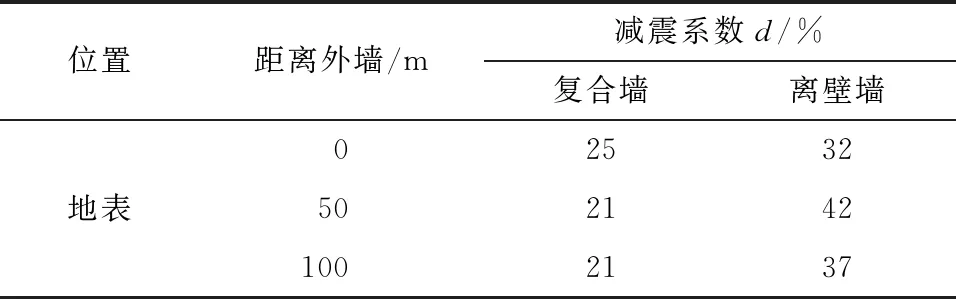
表2 减振系数d

根据以上的结果分析表明，车站采用离壁墙式、叠合墙式、复合墙式结构，地铁产生的环境振动的加速度反应峰值和Z振级由小到大。在传播一定距离以后，地铁产生的环境振动中的高频部分衰减很快，振动优势频率为2 Hz～8 Hz，且环境振动的各频率分量最小的是采用离壁墙式车站方案，复合墙式车站次之，叠合墙式车站各频率分量最大。

2.5 地铁车站不同结构型式经济效益的对比

以国帆路站工程为例，从经济效益角度来考察叠合式结构、复合式结构和离壁墙式结构，主要考虑三种结构的混凝土，砂和钢筋等的用量及造价，将三种方案的综合比较列于表3—表5。

通过数据分析可知，复合式结构比叠合式结构费用增加约6.2%，离壁墙式结构比叠合式结构费用增加约13.8%。

表3 三种结构外包宽度

表4 三种结构主要工程量

表5 费用统计

注：原叠合方案车站主体土建费用11 713万元。

3 结 论

本文以上海轨道交通十号线二期工程国帆路站为工程背景，通过数值仿真计算了叠合墙式、复合墙式、离壁墙式三种结构方案在地铁产生环境振动中各方案的减振效果，并计算三种方案的材料用量和造价，分析得到以下结论。

(1)在传播一定距离以后，地铁产生的环境振动中的高频部分衰减很快，振动优势频率为2 Hz～8 Hz。

(2)采用离壁墙式方案环境振动的各频率分量最小，复合墙式车站次之，叠合墙式车站各频率分量最大。

(3)由于结构内衬墙和外围地下连续墙之间存在着间隙，离壁墙式结构较其他两种方案有效地减少了地铁产生的环境振动。

(4)离壁墙式结构造价是三种结构方案中最高的，但结合它的减振效果，在城市中心对振动要求严格的区域，具有较大应用价值。