基于块体理论的硐室围岩块体稳定性分析程序

周 伟

(四川省核工业地质局二八二大队, 四川 德阳 618000)

目前，地下硐室块体稳定性分析软件[6-8]主要基于将结构面考虑为无限延伸的刚性地质界面的假设条件下进行分析，未考虑其空间发育特征、拟建工程轴线方位以及延伸规模等，分析结果具有不确定性和随机性，需要工程技术人员对主要结构面数据进行比对分析，工作量大且结果可靠性低。但是，技术人员往往关心的是拟建硐室可能发育块体的具体位置、规模等，以便于更为精确的设计，以保证工程施工及运行安全[9-10]。

根据野外搜集调查资料，结合区域地质、工程特性，采用一种简单准确、便于操作，而且能快速分析硐室可能发育的不稳定块体位置、规模、滑动方式、稳定性等相关设计参考参数的硐室块体分析软件是必要的。故本次采用VC++程序编译，结合动态数据库、OPenGL、MFC图形处理功能，开发了一款能快速准确分析硐室围岩块体基本特征参数、稳定性、三维可视化等功能的地下硐室块体稳定性分析程序，具有较好的工程实践性[11]。

1 空间块体边界条件及几何参数的解析

硐室确定性块体解析解是基于块体理论，利用空间结构面、临空面交切，运用数学矢量表达式表示各交切面，通过线性方程组求解[12-16]。块体的几何参数、边界特征，通过矢量计算方程表达，结合结构面物理力学参数计算其稳定性。通过程序语言编辑理论计算公式，利用计算机快速处理数据的计算能力，极大地提高了块体搜索和稳定性分析的效率，且计算结果具有很高的精度。

块体边界条件解析的任务是根据硐室临空面空间方程，结合结构面的空间发育特征，联立求解各方程组唯一实根，该实根即为结构面和硐壁临空面相交形成的顶点。若各方程组均有唯一解，则该组结构面与硐室临空面能形成独立封闭的空间结构体；若方程无解，则该组结构面不能相互交切形成独立块体。

1.1 临空面空间方程数学表达

地下硐室一般为圆拱直墙型，硐室开挖后形成临空面包含两部分(直墙、圆拱)，建立硐室临空面空间模型时，首先建立独立局部坐标系，圆拱的圆心为坐标系的原点，x轴为垂直硐室轴线，y轴为硐室轴线，z轴正方向为竖直向上，R为拱顶圆形半径，l为硐室轴线的长度，α0为正北方向和硐室轴线夹角。则用平面方程和曲面方程表达临空面关系式如下：

(1)

1.2 结构面空间方程的数学表达

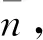
(2)

空间假设采用独立局部坐标系，实测结构面坐标为大地坐标系投影，故需对空间坐标进行转换，转换方程如下：

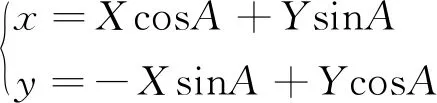
(3)

式中：X，Y代表大地坐标；x,y代表相对局部坐标；A为旋转的角度。

1.3 块体顶点求解

空间复杂块体均可近似为多个四面体组成，可分解为四面体进行矢量分析，故本次考虑的块体主要为四面体块体，形成块体至少需要四个顶点，其中包括一个围岩内部顶点和三个硐壁临空面顶点，块体顶点三维坐标可通过围岩顶点线性方程组求解得到，从而求得相关数值解析解。

块体空间几何形状可根据形成四面体顶点出露位置分为平面四面体、曲面四面体和复合四面体，结合几何参数数学表达式，求解各类四面体的体积大小、重量以及相应重心，以便后续块体分析代用该类参数数值。

2 块体失稳运动方式及稳定性系数解析

2.1 块体失稳运动方式解析

根据块体约束条件和运动学分析，主要为以下四种运动方式：稳定、塌落、单面滑动、双面滑动，块体失稳运动方式的判别主要通过块体各顶点坐标和块体重心的Z值进行对比分析。

设Lz为重心坐标的z值，Tnz为重力线与结构面的交点z坐标，则有：

Tnz=-(pn4+pn1Lx+pn2Ly)/pn3

(4)

(1) 稳定块体和塌落块体判别：

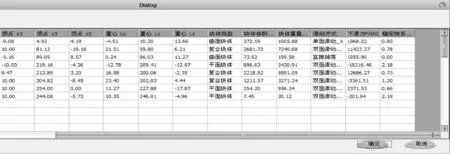
稳定块体判别条件：Tnz

塌落块体判别条件：Tnz>Lz(n=i,j,k)

(5)

(2) 单面滑动块体判别解析：

若min(Lz-Tnz)=Lz-Tiz，则重力矢量与结构面i相交。过Ti点作结构面i的倾向线，其交线Eij、Eik的交点Gi、Gk，z坐标为zgi、zgk，若满足条件Tiz

(3) 双面滑动块体解析解

同理，块体沿两组结构面滑动的判别条件为：

① 若Tiz≥zgi；Tiz≥zgk，则当zgi>zgk，块体沿交线Eij滑动，即沿结构面i、j滑动；当zgi

② 若Tiz≥zgi；Tiz

③ 若Tiz≥zgk；Tiz

2.2 块体稳定性系数解析

单面滑动、双面滑动块体稳定性系数的解析解线性表达式如下式：

(6)

式中：η为稳定性系数；F为下滑力，i、j为结构面编号；Q为块体的重量；β为倾角；C为黏聚力；φ为内摩擦角；S为滑动面面积；Pi为结构面i上的正应力；Pj为结构面j上的正应力；θ为重力与正应力N的夹角。

3 地下硐室块体稳定性分析程序实现

根据软件需求分析，程序设计主要目标，① 程序设计，利用MFC模块设计程序界面，实现软件的数据输入、计算机结果输出和三维可视化功能。② 功能计算分析，根据结构面的组合关系，分析搜索块体并解析块体的几何参数、稳定性等相关参数等。③ 利用OPenGL图形显示功能实现硐室区块体的三维可视化图形输出，具体程序流程如下：

(1) 程序介绍及界面展示。程序主要功能模块为：基本参数数据输入、结构面数据输入、块体搜索及稳定性计算、计算结果输出、空间三维图形显示等。

程序主界面菜单栏包括文件栏、计算栏、视图和帮助，其中文件栏包括新建计算文件、打开计算文件、文件保存和另存储、退出等功能；计算栏包括基本参数输入、结构面数据输入和块体计算指令；视图栏包括块体模型及三维可视化、计算结果的输出。

(2) 基本参数数据设置。地下硐室空间几何特征是确定的，将硐室空间参数作为定值，将其设置为基本输入参数，可简便数据输入步骤，避免重复输入。基本输入参数界面详见图1。

(3) 结构面数据输入。作为块体搜索的重要参数，结构面空间参数包括圆心坐标、产状、延伸规模、物理力学参数等，输入界面格式见图2。本次程序采用动态数据库连接，可直接通过录入好的数据格式直接导入程序，也可在程序界面对其数据进行更改，极大地提高了工作效率和数据录入的准确性。

(4) 块体搜索及稳定性分析。根据块体理论对结构面采用数学矢量化方程表示，并可快速计算块体的顶点坐标，由顶点坐标分析求解块体空间几何特征，判断块体可动性、滑动方式、滑面编号、稳定性系数、下滑力等。

(5) 计算结果输出。本程序计算输出结果格式详见图3—图5，输出结果包括两种格式，一是数据表格格式，二是可视化三维模型格式，其输出结果能直接了解块体空间位置、规模、稳定与否等特征，为工程分析人员提供最直接简单数据支持，且计算结果可通过导出Excel格式的数据表，便于数据处理。

图1 基本参数数据设置

图2 结构面数据输入界面

图3 块体搜索及稳定性求解结果输出界面1

图4 块体搜索及稳定性求解结果输出界面2

4 程序计算结果验证

程序的实用性是决定程序生存的关键所在，为了验证程序实用性，选用已有算例解析解数据对该分析程序进行对比验证。选择验证数据如下：硐室圆拱半径为10 m，硐室跨度为20 m，硐室直墙高度为30 m，硐室长度为260 m，硐室轴线方向与指北经线夹角为180°，岩体密度为2.7 t/m3。算例结构面数据见表1，测试算例结果见表2。

表1 验证程序测试结构面数据

图5 测试算例1#块体三维空间特征示意图

由表2可知，程序验算结果与算例计算各计算结果高度拟合，计算结果误差统计比均小于2.5%，块体顶点坐标及发育方位基本相同，说明程序计算结果可靠。

程序设计考虑了动态数据库连接和界面输出可视化，总体来说，程序数据录入方便，通过已编辑好数据资料直接导入计算，极大的简化了输入数据的繁琐步骤，并降低了数据输入人为错误，程序总体运行效率非常快。得出结论：该分析程序界面友好，程序操作简单，运行效率高，计算结果安全可靠，可直接运用于工程实践过程。

表2 程序验证计算结果表